当前位置：首页 > news >正文

多粒子模型-简单化学反应1

news 2025/11/9 9:35:00

背景

迭代0

迭代1

密闭空间粒子反应仿真代码总结

一、核心仿真场景与设定

二、关键参数设计

三、核心仿真逻辑

1. 反应动力学模型

2. 质量与温度计算逻辑

3. 粒子数量更新规则

四、可视化输出内容

五、代码核心特点

优化空间

一、提升反应物理机制的真实性

1. 粒子运动与碰撞的微观建模（替代当前 “概率性反应”）

2. 温度对粒子行为的精细化影响

3. 反应 stoichiometry（化学计量比）与质量守恒的严格控制

二、优化计算效率（针对大规模粒子仿真）

1. 粒子数量的动态管理（避免冗余计算）

2. 并行计算加速

三、扩展模型功能与可控变量

1. 引入更多环境变量

2. 反应热效应的非线性修正

3. 统计分析功能增强

四、可视化与交互体验优化

1. 动态粒子轨迹展示

2. 多参数敏感性分析界面

3. 数据导出与对比

五、代码结构优化（提升可维护性）

总结

背景

这是一个将化学反应动力学过程进行模拟的模型。初始阶段还是引入了较多的基础化学公式。简单介绍下模型基础内容，将反应物A与反应物B混合，生成反应物C。考虑了包括温度，焓变，比热，化学反应速率，正逆反应等经典化学反应相关的定义。

迭代0

首先交给AI生成初始代码，但AI首先给出的是这样的。

% 粒子反应动力学仿真：A + B <-> C（考虑温度、搅拌、热效应）
clear; clc; close all;%% 1. 反应参数设置
% 基础动力学参数（25℃时）
k_forward0 = 0.05;     % 正向反应速率常数 (L/(mol·s))
k_backward0 = 0.01;    % 逆向反应速率常数 (1/s)
Ea_forward = 40000;    % 正向反应活化能 (J/mol)
Ea_backward = 50000;   % 逆向反应活化能 (J/mol)
delta_H = -15000;      % 反应焓变 (J/mol，负值为放热)% 系统参数
V = 1;                 % 反应体积 (L)
rho = 1000;            % 溶液密度 (kg/m³)
Cp = 4186;             % 比热容 (J/(kg·K))
T_ambient = 298;       % 环境温度 (K)
k_heat = 50;           % 散热系数 (J/(K·s))% 初始条件
C_A0 = 2.0;            % A的初始浓度 (mol/L)
C_B0 = 1.5;            % B的初始浓度 (mol/L)
C_C0 = 0.0;            % C的初始浓度 (mol/L)
T0 = 298;              % 初始温度 (K)
stirring_level = 0.8;  % 搅拌强度 (0-1，影响传质效率)% 时间设置
t_end = 100;           % 仿真总时间 (s)
dt = 0.01;             % 时间步长 (s)
t_span = 0:dt:t_end;%% 2. 反应动力学方程
% 定义微分方程组：dydt = [dC_A/dt; dC_B/dt; dC_C/dt; dT/dt]
function dydt = reaction_kinetics(t, y, params)% 状态变量C_A = y(1);C_B = y(2);C_C = y(3);T = y(4);% 解包参数[k_forward0, k_backward0, Ea_forward, Ea_backward, delta_H, ...V, rho, Cp, T_ambient, k_heat, stirring_level] = params;% 阿累尼乌斯方程计算温度相关的速率常数R = 8.314;  % 气体常数 (J/(mol·K))k_forward = k_forward0 * exp(-Ea_forward/(R*T));k_backward = k_backward0 * exp(-Ea_backward/(R*T));% 搅拌对传质的影响（修正反应速率）k_forward = k_forward * (0.5 + 0.5*stirring_level);  % 搅拌增强传质% 反应速率计算（正向：A+B→C；逆向：C→A+B）r_forward = k_forward * C_A * C_B;    % 正向反应速率r_backward = k_backward * C_C;        % 逆向反应速率r_net = r_forward - r_backward;       % 净反应速率% 浓度变化率dC_A_dt = -r_net;dC_B_dt = -r_net;dC_C_dt = r_net;% 温度变化（反应热 + 散热）heat_generated = -delta_H * V * r_net;  % 反应产热速率 (J/s)heat_loss = k_heat * (T - T_ambient);   % 散热速率 (J/s)dT_dt = (heat_generated - heat_loss) / (rho * V * Cp);  % 温度变化率dydt = [dC_A_dt; dC_B_dt; dC_C_dt; dT_dt];
end%% 3. 数值求解
params = [k_forward0, k_backward0, Ea_forward, Ea_backward, delta_H, ...V, rho, Cp, T_ambient, k_heat, stirring_level];
y0 = [C_A0; C_B0; C_C0; T0];  % 初始状态向量% 使用ode45求解微分方程组
[t, y] = ode45(@(t,y) reaction_kinetics(t,y,params), t_span, y0);% 提取结果
C_A = y(:,1);
C_B = y(:,2);
C_C = y(:,3);
T = y(:,4);%% 4. 结果可视化
figure('Name','反应浓度变化','Position',[100,100,800,500]);
plot(t, C_A, 'r-', t, C_B, 'b-', t, C_C, 'g-', 'LineWidth',1.5);
xlabel('时间 (s)'); ylabel('浓度 (mol/L)');
legend('粒子A','粒子B','粒子C'); grid on;
title('反应过程中各粒子浓度变化');figure('Name','反应温度变化','Position',[100,650,800,300]);
plot(t, T-273.15, 'k-', 'LineWidth',1.5);  % 转换为摄氏度
xlabel('时间 (s)'); ylabel('温度 (℃)');
grid on; title('反应过程中温度变化');% 计算平衡常数随温度的变化（验证范特霍夫方程）
K_eq = (k_forward0/k_backward0) * exp((Ea_backward - Ea_forward)/(8.314*T));
figure('Name','平衡常数变化','Position',[950,100,800,300]);
plot(t, K_eq, 'm-', 'LineWidth',1.5);
xlabel('时间 (s)'); ylabel('平衡常数 K');
grid on; title('反应平衡常数随时间（温度）的变化');%% 5. 搅拌强度影响分析（可选）
if false  % 设为true运行此分析stirring_levels = [0.2, 0.5, 0.8, 1.0];figure('Name','搅拌强度影响','Position',[950,450,800,500]);for i = 1:length(stirring_levels)params(11) = stirring_levels(i);[t, y] = ode45(@(t,y) reaction_kinetics(t,y,params), t_span, y0);plot(t, y(:,3), 'LineWidth',1.2); hold on;endxlabel('时间 (s)'); ylabel('C的浓度 (mol/L)');legend(arrayfun(@(x) sprintf('搅拌强度=%.1f',x), stirring_levels,'UniformOutput',false));grid on; title('不同搅拌强度对产物C生成的影响');
end

这是一个基础的动力学方程进行的模拟，非常成熟的公式，但是不符合我们的主题，我们需要离散化，也就是多粒子。

迭代1

% 密闭空间粒子反应仿真（每个粒子1g，无阿伏伽德罗常数）
clear; clc; close all;%% 1. 基本参数设置
% 粒子初始数量（每个粒子质量=1g）
N_A0 = 1000;    % A粒子初始数量（总质量1000g）
N_B0 = 1000;    % B粒子初始数量（总质量1000g）
N_C0 = 0;       % C粒子初始数量% 反应动力学参数
k_forward0 = 0.001;   % 基础反应速率常数 (1/s)
k_backward0 = 0.0002; % 逆反应基础速率常数 (1/s)
Ea_forward = 30000;   % 正向反应活化能 (J/kg) （修改为单位质量活化能）
Ea_backward = 45000;  % 逆向反应活化能 (J/kg)
delta_H = -20000;     % 反应焓变 (J/kg) （每kg反应物质的能量变化，负值放热）% 系统参数（密闭空间，无散热）
V = 0.1;               % 反应体积 (L)
T0 = 298;              % 初始温度 (K)
rho = 1000;            % 密度 (kg/m³)
Cp = 4186;             % 比热容 (J/(kg·K))
stirring_level = 0.7;  % 搅拌强度 (0-1)% 时间参数
t_total = 300;         % 总仿真时间 (s)
dt = 0.1;              % 时间步长 (s)
t = 0:dt:t_total;
n_steps = length(t);%% 2. 初始化数组
N_A = zeros(1, n_steps);
N_B = zeros(1, n_steps);
N_C = zeros(1, n_steps);
T = zeros(1, n_steps);% 初始条件
N_A(1) = N_A0;
N_B(1) = N_B0;
N_C(1) = N_C0;
T(1) = T0;%% 3. 反应仿真循环（每个粒子1g，简化质量计算）
R = 8.314;  % 气体常数 (J/(kg·K)) （此处保留单位一致性）
for i = 1:n_steps-1% 当前粒子数量和温度na = N_A(i);nb = N_B(i);nc = N_C(i);temp = T(i);% 计算温度相关的速率常数（阿累尼乌斯方程）k_forward = k_forward0 * exp(-Ea_forward/(R*temp));k_backward = k_backward0 * exp(-Ea_backward/(R*temp));% 搅拌影响：提高粒子碰撞概率collision_factor = 0.3 + 0.7*stirring_level;  % 0.3-1.0之间k_forward = k_forward * collision_factor * (na*nb)/(V^2);  % 与A、B粒子数乘积成正比k_backward = k_backward * collision_factor * nc/V;         % 与C粒子数成正比% 计算单位时间反应概率P_forward = 1 - exp(-k_forward * dt);  % 正向反应概率P_backward = 1 - exp(-k_backward * dt);% 逆向反应概率% 随机发生正向反应（A + B → C）max_possible_forward = min(na, nb);  % 最大可能反应的粒子数n_react_forward = binornd(max_possible_forward, P_forward);n_react_forward = min(n_react_forward, max_possible_forward);% 随机发生逆向反应（C → A + B）max_possible_backward = nc;  % 最大可能分解的C粒子数n_react_backward = binornd(max_possible_backward, P_backward);n_react_backward = min(n_react_backward, max_possible_backward);% 更新粒子数量N_A(i+1) = na - n_react_forward + n_react_backward;N_B(i+1) = nb - n_react_forward + n_react_backward;N_C(i+1) = nc + n_react_forward - n_react_backward;% 温度变化（每个粒子1g，直接用粒子数计算质量）mass_react = (n_react_forward - n_react_backward) / 1000;  % 反应质量（kg，1粒子=1g）heat_gen = -delta_H * mass_react;  % 反应产热 (J)（放热反应为正值）system_mass = (na + nb + nc) / 1000;  % 系统总质量 (kg)delta_T = heat_gen / (system_mass * Cp);  % 温度变化（密闭空间无散热）T(i+1) = temp + delta_T;
end%% 4. 结果可视化
figure('Position',[100,100,1000,600]);
subplot(2,1,1);
plot(t, N_A, 'r-', t, N_B, 'b-', t, N_C, 'g-', 'LineWidth',1.5);
xlabel('时间 (s)'); ylabel('粒子数量');
legend('A粒子','B粒子','C粒子'); grid on;
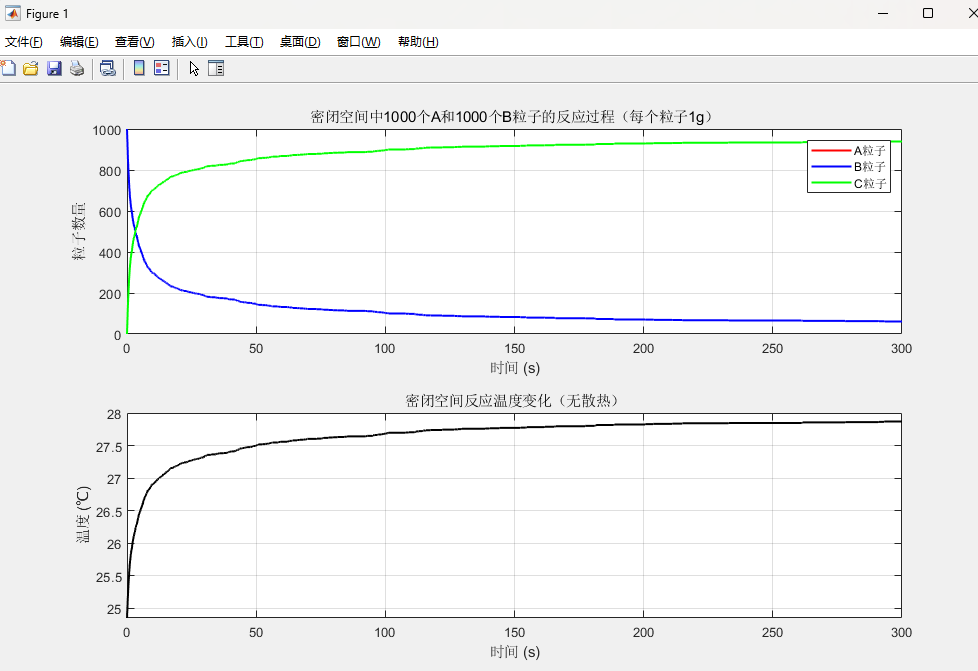
title('密闭空间中1000个A和1000个B粒子的反应过程（每个粒子1g）');subplot(2,1,2);
plot(t, T-273.15, 'k-', 'LineWidth',1.5);
xlabel('时间 (s)'); ylabel('温度 (℃)');
grid on; title('密闭空间反应温度变化（无散热）');
set(gcf, 'PaperPositionMode', 'auto');% 搅拌强度影响分析
figure('Position',[100,750,1000,500]);
stir_levels = [0.2, 0.5, 0.8, 1.0];
colors = lines(length(stir_levels));
for s = 1:length(stir_levels)N_C_stir = zeros(1, n_steps);N_C_stir(1) = N_C0;Na = N_A0; Nb = N_B0; Nc = N_C0;Temp = T0;for i = 1:n_steps-1% 计算速率常数kf = k_forward0 * exp(-Ea_forward/(R*Temp)) * ...(0.3 + 0.7*stir_levels(s)) * (Na*Nb)/(V^2);kb = k_backward0 * exp(-Ea_backward/(R*Temp)) * ...(0.3 + 0.7*stir_levels(s)) * Nc/V;% 反应概率Pf = 1 - exp(-kf * dt);Pb = 1 - exp(-kb * dt);% 反应粒子数max_f = min(Na, Nb);nr_f = binornd(max_f, Pf);nr_f = min(nr_f, max_f);max_b = Nc;nr_b = binornd(max_b, Pb);nr_b = min(nr_b, max_b);% 更新粒子数Na = Na - nr_f + nr_b;Nb = Nb - nr_f + nr_b;Nc = Nc + nr_f - nr_b;N_C_stir(i+1) = Nc;% 温度变化（每个粒子1g）mass_r = (nr_f - nr_b)/1000;  % 反应质量(kg)heat_g = -delta_H * mass_r;sys_mass = (Na + Nb + Nc)/1000;  % 系统总质量(kg)Temp = Temp + heat_g/(sys_mass * Cp);endplot(t, N_C_stir, 'Color', colors(s,:), 'LineWidth',1.2); hold on;
end
xlabel('时间 (s)'); ylabel('C粒子数量');
legend(arrayfun(@(x) sprintf('搅拌强度=%.1f',x), stir_levels,'UniformOutput',false));
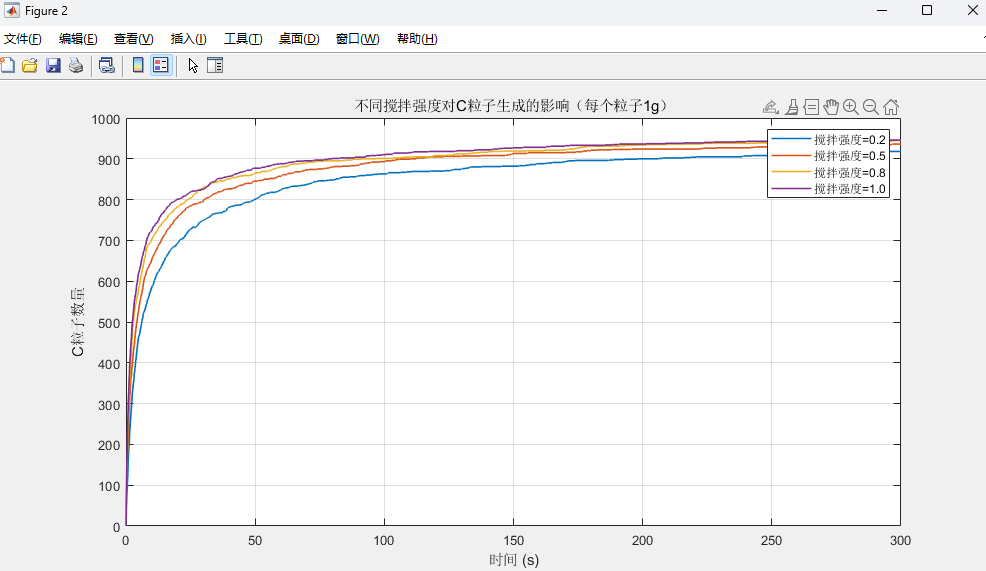
grid on; title('不同搅拌强度对C粒子生成的影响（每个粒子1g）');

经过不断努力，将最小单位离散为1g（这里我本来是想弄成0.01mol，但是这个版本结果不理想，没有贴出来）。

密闭空间粒子反应仿真代码总结

一、核心仿真场景与设定

本代码用于模拟密闭空间内粒子反应过程，核心设定聚焦 “简化质量计算” 与 “无散热环境”，具体如下：

反应体系：1000 个 A 粒子（总质量 1000g）与 1000 个 B 粒子（总质量 1000g）可逆反应生成 C 粒子（A+B ↔ C）
简化规则：每个粒子质量固定为 1g，不涉及阿伏伽德罗常数，直接通过粒子数量计算质量相关物理量
环境特性：密闭空间无散热，反应产生的热量全部用于系统温度变化，无对外热量交换

二、关键参数设计

参数类别核心参数及说明
初始条件粒子初始数量：N_A0=1000、N_B0=1000、N_C0=0；初始温度 T0=298K（25℃）
动力学参数基础速率常数：正向 k_forward0=0.001 1/s、逆向 k_backward0=0.0002 1/s；活化能（单位质量）：Ea_forward=30000 J/kg、Ea_backward=45000 J/kg；反应焓变（单位质量）：delta_H=-20000 J/kg（负值表示放热）
系统参数反应体积 V=0.1L，密度 rho=1000 kg/m³，比热容 Cp=4186 J/(kg・K)；搅拌强度 stirring_level=0.7（0-1 区间，表征碰撞概率提升程度）
时间参数仿真总时长 t_total=300s，时间步长 dt=0.1s，确保反应过程细节被捕捉

三、核心仿真逻辑

1. 反应动力学模型

温度对速率的影响：通过阿累尼乌斯方程计算温度依赖的速率常数，温度升高会加速正、逆反应（符合动力学规律）
搅拌的作用：通过 “碰撞因子”（0.3+0.7× 搅拌强度）修正反应速率，搅拌越强，粒子碰撞概率越高，反应速率越快
可逆反应控制：分别计算正向反应（A+B→C）和逆向反应（C→A+B）的发生概率，通过二项分布随机生成实际反应粒子数，确保反应随机性与合理性

2. 质量与温度计算逻辑

质量计算：直接通过粒子数量换算质量（1 粒子 = 1g），反应质量 =（正向反应粒子数 - 逆向反应粒子数）/1000（单位转换为 kg）
温度变化：密闭空间无散热，温度变化仅由反应热决定 —— 放热反应使温度升高，吸热反应使温度降低，公式为：delta_T = 反应产热 /(系统总质量 × 比热容)，系统总质量通过当前 A、B、C 粒子总数换算得到

3. 粒子数量更新规则

正向反应：最大可能反应数受限于当前 A、B 粒子数的最小值，实际反应数由二项分布随机生成（不超过最大值）
逆向反应：最大可能分解数为当前 C 粒子数，实际分解数由二项分布随机生成（不超过最大值）
数量更新：A、B 粒子数 = 当前数 - 正向反应数 + 逆向反应数；C 粒子数 = 当前数 + 正向反应数 - 逆向反应数

四、可视化输出内容

代码生成 3 类核心图表，直观展示反应过程：

粒子数量动态变化图：同一图中展示 A（红色）、B（蓝色）、C（绿色）粒子数随时间的变化，可观察 “A、B 减少→C 先增后稳” 的平衡过程
系统温度变化图：展示温度（℃）随时间的变化，放热反应下温度持续升高至反应平衡后趋于稳定
搅拌强度影响图：对比 4 种搅拌强度（0.2、0.5、0.8、1.0）下 C 粒子数的生成曲线，清晰体现 “搅拌越强，反应达到平衡越快、C 粒子生成效率越高”

五、代码核心特点

简化性：以 “1 粒子 = 1g” 规避复杂的摩尔质量计算，无阿伏伽德罗常数依赖，降低理解与计算难度
真实性：兼顾温度、搅拌对反应速率的影响，以及正逆反应的动态平衡，符合实际反应动力学规律
直观性：可视化结果清晰呈现粒子变化、温度变化及搅拌的影响，便于分析反应特性

参数类别	核心参数及说明
初始条件	粒子初始数量：N_A0=1000、N_B0=1000、N_C0=0；初始温度 T0=298K（25℃）
动力学参数	基础速率常数：正向 k_forward0=0.001 1/s、逆向 k_backward0=0.0002 1/s；活化能（单位质量）：Ea_forward=30000 J/kg、Ea_backward=45000 J/kg；反应焓变（单位质量）：delta_H=-20000 J/kg（负值表示放热）
系统参数	反应体积 V=0.1L，密度 rho=1000 kg/m³，比热容 Cp=4186 J/(kg・K)；搅拌强度 stirring_level=0.7（0-1 区间，表征碰撞概率提升程度）
时间参数	仿真总时长 t_total=300s，时间步长 dt=0.1s，确保反应过程细节被捕捉

优化空间

对于本次模拟，还没有达到我想象中的状态，主要是对于微观粒子的交互。目前主要是以概率或者反应速率的形式来离散化整个过程；而我主要想要的是微观化，形式可以是碰撞，甚至是涉及化学键断裂等等。

以下是AI给出的优化方案

对粒子反应仿真模型的优化可以从物理真实性提升、计算效率改进、功能扩展性和可视化增强四个维度展开，以下是具体优化方向及实现思路：

一、提升反应物理机制的真实性

1. 粒子运动与碰撞的微观建模（替代当前 “概率性反应”）

问题：当前模型通过 “反应概率 × 粒子数” 间接模拟反应，未体现粒子的空间位置和运动特性。
优化方案：
引入粒子坐标系统：为每个粒子分配 2D/3D 空间坐标（如x_A, y_A为 A 粒子位置），初始随机分布在反应容器内。
模拟粒子运动：基于扩散（如布朗运动，dx = sqrt(2*D*dt)*randn，D为扩散系数）或搅拌流场（如旋转流场v = [ω*y, -ω*x]，ω为搅拌角速度）计算粒子位移。
碰撞检测与反应触发：当 A、B 粒子距离小于临界半径（如分子直径r0）时，以概率P_forward触发正向反应；C 粒子自发分解概率为P_backward。

优势：直接体现搅拌对粒子空间分布的影响（搅拌越强，粒子混合越均匀，碰撞频率越高），反应更贴近微观物理过程。

2. 温度对粒子行为的精细化影响

问题：当前仅通过阿累尼乌斯方程影响反应速率，未体现温度对粒子运动的影响。
优化方案：
温度与扩散系数耦合：扩散系数D ∝ T（温度升高，粒子热运动加剧，扩散加快），即D = D0 * (T/T0)（D0为参考温度下的扩散系数）。
系统内能分布：将总热量分配到每个粒子的动能中（KE ∝ T），粒子运动速度随温度升高而增大，进一步提升碰撞概率。

3. 反应 stoichiometry（化学计量比）与质量守恒的严格控制

问题：当前假设 1A+1B→1C，若反应式更复杂（如 2A+B→C），现有粒子数更新逻辑不适用。
优化方案：
定义反应计量矩阵：如[ -2, -1, 1 ]表示 2A + B → C，正向反应时 A 减少 2n、B 减少 n、C 增加 n；逆向反应则相反。
质量守恒校验：由于每个粒子质量固定，总质量(N_A + N_B + N_C)×1g应守恒（忽略反应质量亏损），代码中添加实时校验机制。

二、优化计算效率（针对大规模粒子仿真）

1. 粒子数量的动态管理（避免冗余计算）

问题：当粒子数达 10^5 以上时，循环中遍历每个粒子会导致计算缓慢。
优化方案：
分组管理粒子：将同类粒子按空间网格分组（如划分 10×10 网格），仅检测同一网格内的粒子碰撞（减少跨网格无效计算）。
稀疏表示法：用数组存储存在的粒子（如删除已反应的粒子索引），避免对 “0 粒子” 的无效计算。

2. 并行计算加速

适用场景：当粒子数超过 10^4 时，可利用 MATLAB 的parfor并行循环。
实现：将粒子分成若干子集，并行计算每个子集的运动、碰撞和反应，最后合并结果（需注意并行随机数的独立性）。

三、扩展模型功能与可控变量

1. 引入更多环境变量

容器形状与边界条件：如圆柱形容器（粒子碰到边界时反弹）、非均匀搅拌（容器边缘搅拌强度低于中心）。
初始非均匀分布：模拟 A、B 粒子初始分层（如 A 在底部、B 在上层），观察搅拌对混合效率的影响。
多阶段反应：扩展反应链（如 A+B→C，C+D→E），需新增粒子类型（D、E）及相应反应参数。

2. 反应热效应的非线性修正

问题：当前假设比热容Cp为常数，实际中Cp可能随温度变化（如高温下物质比热容改变）。
优化方案：引入Cp(T)函数（如多项式拟合Cp = a + b*T + c*T²），使温度计算更准确。

3. 统计分析功能增强

增加反应动力学参数反演：通过仿真结果拟合实际反应的k_forward、Ea_forward等参数（利用最小二乘法）。
输出关键指标：如反应达到平衡的时间、最大反应速率、温度峰值等，便于不同参数组合的对比。

四、可视化与交互体验优化

1. 动态粒子轨迹展示

用动画实时显示粒子运动（如plot(x_A, y_A, 'ro', x_B, y_B, 'bo', x_C, y_C, 'go')，配合pause(dt)），直观观察搅拌对混合的影响。
可调节动画速度、视角（3D 模型时），或暂停 / 重启仿真以分析关键时刻的粒子分布。

2. 多参数敏感性分析界面

设计交互控件（如滑块uicontrol('Style','slider')），实时调节搅拌强度、初始温度、活化能等参数，动态更新仿真结果。
生成参数 - 结果响应曲面（如搅拌强度 - 温度峰值曲面图），快速定位关键影响因素。

3. 数据导出与对比

将粒子数、温度等数据导出为 CSV 文件，支持与实验数据对比（如计算仿真与实验的均方误差）。
自动生成多组参数下的对比图表（如不同初始温度下的 C 粒子生成曲线），用subplot或legend区分。

五、代码结构优化（提升可维护性）

模块化封装：将 “粒子运动”“碰撞检测”“反应计算”“温度更新” 等功能拆分为独立函数（如[particles] = particle_motion(particles, D, dt)），便于单独调试和修改。
参数配置文件：将所有参数存入结构体或外部.m文件（如params.m），避免在主代码中硬编码，方便批量修改和参数扫描。

总结

优化优先级可根据需求确定：

若侧重微观真实性，优先实现粒子空间运动与碰撞检测；
若需大规模仿真，重点优化计算效率（并行、分组管理）；
若用于教学或演示，则强化动态可视化与交互控件。

通过上述优化，模型可从 “基于概率的宏观模拟” 升级为 “兼顾微观运动与宏观特性的精细化仿真”，适用场景更广（如化学反应工程、粒子扩散研究等）。