当前位置：首页 > news >正文

算法数学---差分数组（Difference Array）

news 2025/11/8 12:41:57

差分数组是一种用于高效处理区间更新和单点查询的数据结构，其核心思想是通过记录数组元素间的差值，将原本需要O(n)时间的区间更新操作优化为O(1)。

差分数组

一、差分数组的定义

对于一个长度为n的原数组A（下标从0开始），其差分数组D的定义为：

当i = 0时，D[0] = A[0]；
当i > 0时，D[i] = A[i] - A[i-1]。

即差分数组D的每个元素记录了原数组A中当前元素与前一个元素的差值。通过这一特性，原数组A可以由差分数组D的前缀和还原：
$\sum_{k=0}^{i} D[k]$

例如，若原数组A = [1, 3, 6, 10, 15]，则差分数组D的计算过程为：

D[0] = A[0] = 1
D[1] = A[1] - A[0] = 3 - 1 = 2
D[2] = A[2] - A[1] = 6 - 3 = 3
D[3] = A[3] - A[2] = 10 - 6 = 4
D[4] = A[4] - A[3] = 15 - 10 = 5

因此D = [1, 2, 3, 4, 5]，而通过D的前缀和计算A：

A[0] = D[0] = 1
A[1] = D[0] + D[1] = 1 + 2 = 3
A[2] = 1 + 2 + 3 = 6（与原数组一致）。

二、核心操作

差分数组的优势体现在区间更新和原数组还原两个操作上

1. 初始化差分数组

根据定义，初始化差分数组需要遍历原数组，计算相邻元素的差值。时间复杂度为O(n)。

vector<int> initDiffArray(const vector<int>& A) {int n = A.size();vector<int> D(n);D[0] = A[0];for (int i = 1; i < n; ++i) {D[i] = A[i] - A[i-1];}return D;
}

2. 区间更新（核心优化点）

假设需要对原数组A的区间[L, R]（闭区间）内所有元素加上一个值v（v可正可负，实现减法），直接操作原数组需要遍历[L, R]，时间复杂度为O(R-L+1)；而通过差分数组只需2步操作（在L出+v，在R+1处-v），时间复杂度为O(1)。

操作原理：
对A[L..R]加v，等价于：

D[L] += v：从L开始，所有元素的前缀和都会增加v（因为A[L]及之后的元素都包含D[L]）；
D[R+1] -= v（若R+1 < n）：从R+1开始，前缀和增加的v被抵消（保证R之后的元素不受影响）。

例如，对A = [1, 3, 6, 10, 15]的[1, 3]区间加2：

原D = [1, 2, 3, 4, 5]
执行D[1] += 2 → D[1] = 4
执行D[4] -= 2（因R=3，R+1=4 < 5）→ D[4] = 3
新D = [1, 4, 3, 4, 3]
还原A：A[0]=1，A[1]=1+4=5，A[2]=1+4+3=8，A[3]=1+4+3+4=12，A[4]=1+4+3+4+3=15。可见[1,3]元素均加了2（3→5，6→8，10→12），符合预期。

代码实现：

void rangeUpdate(vector<int>& D, int L, int R, int v) {int n = D.size();if (L < 0 || R >= n || L > R) return; // 处理无效区间D[L] += v;if (R + 1 < n) { // 避免越界D[R + 1] -= v;}
}

3. 还原原数组（单点/全量查询）

通过差分数组的前缀和可还原原数组，若只需查询A[i]，计算D[0..i]的前缀和即可；若需全量查询，遍历计算前缀和数组即可。时间复杂度为O(n)（全量）或O(i)（单点）。

vector<int> restoreArray(const vector<int>& D) {int n = D.size();vector<int> A(n);A[0] = D[0];for (int i = 1; i < n; ++i) {A[i] = A[i-1] + D[i]; // 前缀和累加}return A;
}

三、差分数组的性质

与原数组的互逆性：差分数组是原数组的“差”，原数组是差分数组的“前缀和”，二者互为逆操作。
区间更新的高效性：将区间更新从O(n)优化为O(1)，这是差分数组的核心价值。尤其当存在大量区间更新（如10^5次）时，效率提升极为显著（从O(10^10)降至O(10^5)）。
适合离线场景：差分数组的优势在于“先积累所有更新，最后一次性还原”。若需要频繁在更新过程中查询中间结果（如边更新边查A[i]），则每次查询需O(n)时间，效率较低（此时更适合线段树或树状数组）。
边界敏感性：当R = n-1（区间包含最后一个元素）时，R+1 = n已超出数组范围，此时无需执行D[R+1] -= v（因前缀和计算不会涉及D[n]），代码需特殊处理。
空间复杂度：与原数组同规模，为O(n)，无额外空间开销。

四、适用场景与对比

差分数组的适用场景需满足：

以区间更新（如[L, R]加/减v）为主；
查询为单点查询或全量查询，且查询频率远低于更新频率；
数据规模较大（如n > 10^4），需要优化时间复杂度。

与其他数据结构的对比：

数据结构	区间更新	单点查询	区间查询	适用场景
差分数组	O(1)	O(n)	O(n)	大量区间更新+最后全量查询
前缀和数组	O(n)	O(1)	O(1)	大量单点更新+大量区间查询
线段树	O(logn)	O(logn)	O(logn)	动态更新+频繁中间查询

完整示例代码

以下代码演示差分数组的初始化、多次区间更新及原数组还原过程：

#include <iostream>
#include <vector>
using namespace std;// 初始化差分数组
vector<int> initDiffArray(const vector<int>& A) {int n = A.size();vector<int> D(n);D[0] = A[0];for (int i = 1; i < n; ++i) {D[i] = A[i] - A[i-1];}return D;
}// 区间更新：A[L..R] += v
void rangeUpdate(vector<int>& D, int L, int R, int v) {int n = D.size();if (L < 0 || R >= n || L > R) {cerr << "无效区间！" << endl;return;}D[L] += v;if (R + 1 < n) {D[R + 1] -= v;}
}// 从差分数组还原原数组
vector<int> restoreArray(const vector<int>& D) {int n = D.size();vector<int> A(n);A[0] = D[0];for (int i = 1; i < n; ++i) {A[i] = A[i-1] + D[i];}return A;
}int main() {// 原数组vector<int> A = {10, 20, 30, 40, 50};cout << "初始数组: ";for (int num : A) cout << num << " ";cout << endl;// 初始化差分数组vector<int> D = initDiffArray(A);cout << "初始差分数组: ";for (int num : D) cout << num << " ";cout << endl;// 执行多次区间更新rangeUpdate(D, 1, 3, 5);   // [1,3]加5rangeUpdate(D, 0, 2, -3);  // [0,2]减3rangeUpdate(D, 4, 4, 10);  // [4,4]加10（单点更新）cout << "更新后差分数组: ";for (int num : D) cout << num << " ";cout << endl;// 还原原数组vector<int> newA = restoreArray(D);cout << "更新后数组: ";for (int num : newA) cout << num << " ";cout << endl;return 0;
}

输出结果：

初始数组: 10 20 30 40 50 
初始差分数组: 10 10 10 10 10 
更新后差分数组: 7 12 12 5 -5 
更新后数组: 7 19 31 36 60

验证：

初始A = [10,20,30,40,50]
第一次更新[1,3] +5：通过差分数组操作后，对应原数组中索引1-3的元素会增加5；
第二次更新[0,2] -3：索引0-2的元素会减少3；
第三次更新[4,4] +10：索引4的元素增加10；
最终通过差分数组前缀和还原的[7,19,31,36,60]符合所有更新逻辑，体现了差分数组的准确性。

差分数组是处理区间更新的“利器”，其核心在于通过记录差值将高频区间操作优化为常数时间。掌握差分数组需理解“差与前缀和的互逆关系”，并明确其适用场景（离线、大量更新、少查询）。在实际应用中，结合二维扩展和边界处理，可有效解决矩阵更新、区间统计等问题。

二维差分数组

二维差分分数组是一维差分分数组在二维场景的扩展，专门用于高效处理矩形区域更新（如对矩阵中某个矩形内的所有元素加/减一个值）和全量还原查询。其核心思想是通过记录二维前缀和的差值，将原本需要O(ab)时间的矩形更新（a、b为矩形的行数和列数）优化为O(1)，在图像处理、矩阵统计等场景中应用广泛。

一、二维差分分数组的定义

对于一个n行m列的二维原数组A（下标从0开始），其二维差分分数组D（同样为n行m列）的定义基于二维前缀和的逆运算：
原数组A是差分分数组D的二维前缀和，即A[i][j]等于D中从(0,0)到(i,j)的所有元素之和。用公式表示为：
$\sum_{x=0}^i \sum_{y=0}^j D[x][y]$

这一关系是二维差分分数组的核心——与一维类似，D记录了A的“差值信息”，而A可通过D的二维前缀和还原。

二、二维差分分数组的构造（从A到D）

构造二维差分分数组的本质是求解“如何从原数组A推导出D”，需要基于二维前缀和的逆运算推导公式。

推导过程：

已知A是D的二维前缀和，即：

当i=0且j=0时：A[0][0] = D[0][0]（因为只有D[0][0]一个元素）。
当i=0且j>0时（第一行）：A[0][j] = A[0][j-1] + D[0][j]（仅需累加当前行的前序元素），因此D[0][j] = A[0][j] - A[0][j-1]。
当j=0且i>0时（第一列）：A[i][0] = A[i-1][0] + D[i][0]（仅需累加当前列的前序元素），因此D[i][0] = A[i][0] - A[i-1][0]。
当i>0且j>0时（非边界元素）：A[i][j]的二维前缀和需包含A[i-1][j]（上方区域）、A[i][j-1]（左方区域），但A[i-1][j-1]被重复累加，因此需要减去。即：
$A [i] [j] = A [i - 1] [j] + A [i] [j - 1] - A [i - 1] [j - 1] + D [i] [j]$
整理得：
$D [i] [j] = A [i] [j] - A [i - 1] [j] - A [i] [j - 1] + A [i - 1] [j - 1]$

构造公式总结：

$\begin{cases} A[0][0] & \text{if } i=0 \text{ and } j=0, \\ A[0][j] - A[0][j-1] & \text{if } i=0 \text{ and } j>0, \\ A[i][0] - A[i-1][0] & \text{if } j=0 \text{ and } i>0, \\ A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1] & \text{if } i>0 \text{ and } j>0. \end{cases}$

示例：

设原数组A为3行3列矩阵：

A = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]

按公式构造D：

D[0][0] = A[0][0] = 1
D[0][1] = A[0][1] - A[0][0] = 2 - 1 = 1
D[0][2] = A[0][2] - A[0][1] = 3 - 2 = 1
D[1][0] = A[1][0] - A[0][0] = 4 - 1 = 3
D[1][1] = A[1][1] - A[0][1] - A[1][0] + A[0][0] = 5 - 2 - 4 + 1 = 0
D[1][2] = A[1][2] - A[0][2] - A[1][1] + A[0][1] = 6 - 3 - 5 + 2 = 0
D[2][0] = A[2][0] - A[1][0] = 7 - 4 = 3
D[2][1] = A[2][1] - A[1][1] - A[2][0] + A[1][0] = 8 - 5 - 7 + 4 = 0
D[2][2] = A[2][2] - A[1][2] - A[2][1] + A[1][1] = 9 - 6 - 8 + 5 = 0

因此，差分分数组D为：

D = [[1, 1, 1],[3, 0, 0],[3, 0, 0]
]

三、二维差分分数组的还原（从D到A）

还原过程即计算D的二维前缀和，步骤为：先对D的每一行计算行前缀和，再对结果计算列前缀和（或先列后行，结果一致）。

具体步骤：

行前缀和：对D的每一行，从左到右累加，得到中间矩阵row_sum，其中row_sum[i][j] = row_sum[i][j-1] + D[i][j]（j=0时row_sum[i][0] = D[i][0]）。
列前缀和：对row_sum的每一列，从上到下累加，得到原数组A，其中A[i][j] = A[i-1][j] + row_sum[i][j]（i=0时A[0][j] = row_sum[0][j]）。

示例验证（还原上述D为A）：

计算D的行前缀和row_sum：
- 第0行：[1, 1+1=2, 2+1=3]
- 第1行：[3, 3+0=3, 3+0=3]
- 第2行：[3, 3+0=3, 3+0=3]
计算row_sum的列前缀和A：
- 第0列：[1, 1+3=4, 4+3=7]
- 第1列：[2, 2+3=5, 5+3=8]
- 第2列：[3, 3+3=6, 6+3=9]
结果与原数组A完全一致，验证了还原逻辑的正确性。

四、矩形区域更新（核心操作）

二维差分分数组的核心价值是O(1)时间完成矩形区域更新。假设需要对原数组A中左上角(x1,y1)、右下角(x2,y2)的矩形区域内所有元素加v（v可正可负），通过差分分数组D只需4步操作。

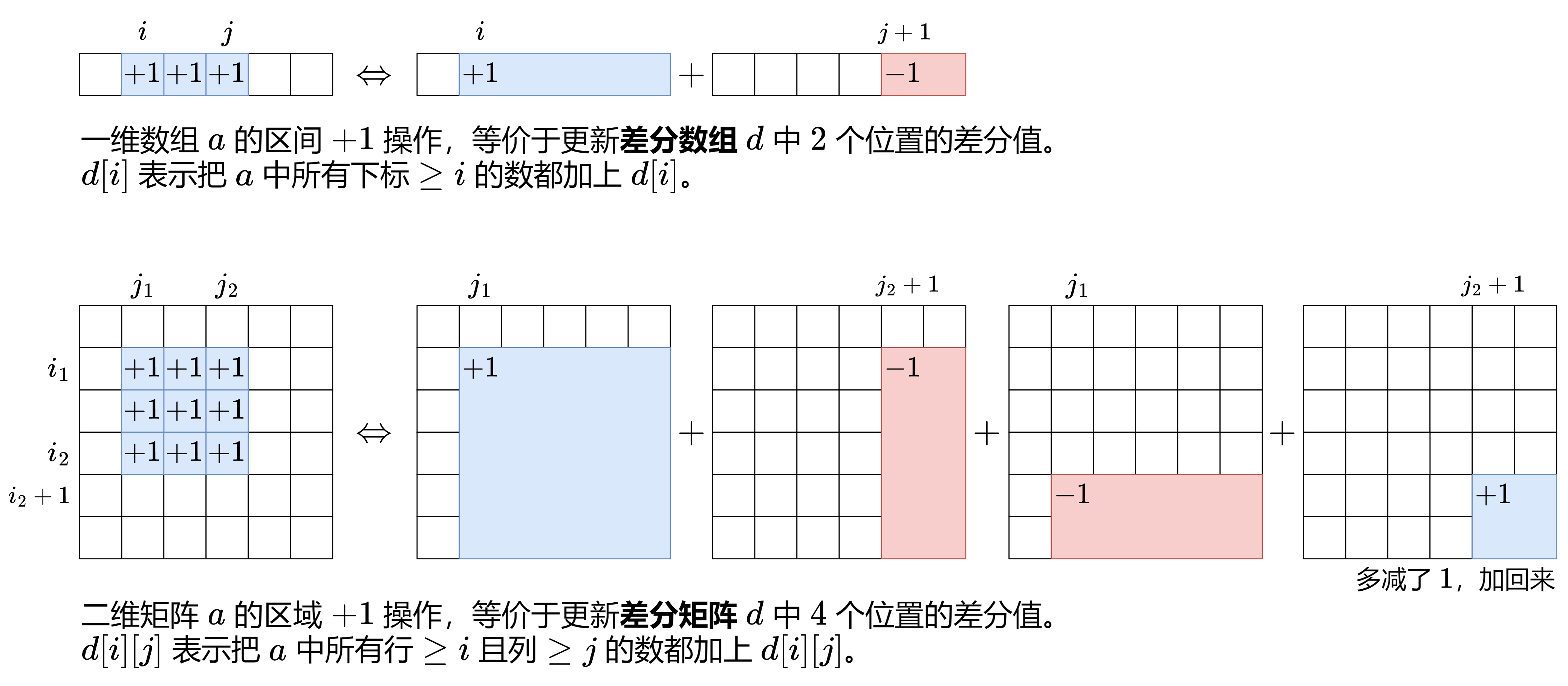
在这里插入图片描述
图片是引用的灵神题解的图片

更新原理：

矩形更新的本质是让A中目标区域的所有元素在还原时都增加v。由于A是D的二维前缀和，需通过D的4个关键点控制前缀和的累加范围：

D[x1][y1] += v：从(x1,y1)开始，所有右下方的元素（包含目标矩形）的前缀和都会增加v。
D[x1][y2+1] -= v：从(x1,y2+1)开始，抵消右侧区域的v（保证目标矩形右侧不受影响）。
D[x2+1][y1] -= v：从(x2+1,y1)开始，抵消下方区域的v（保证目标矩形下方不受影响）。
D[x2+1][y2+1] += v：由于(x2+1,y2+1)被上述两次抵消重复减去了v，此处需加回v以恢复平衡。

边界处理：

若x2+1 >= n（超出行数）或y2+1 >= m（超出列数），则无需处理对应位置（因前缀和计算不会涉及这些超出范围的元素）。

示例：

对上述A中(1,1)到(2,2)的矩形区域（元素5,6,8,9）加2，步骤如下：

原D为：
```
[[1, 1, 1],[3, 0, 0],[3, 0, 0]
]
```
矩形区域x1=1,y1=1，x2=2,y2=2，执行更新：
- D[1][1] += 2 → 0+2=2
- y2+1=3（超出列数m=3），跳过D[x1][y2+1] -=v
- x2+1=3（超出行数n=3），跳过D[x2+1][y1] -=v
- 同上，跳过D[x2+1][y2+1] +=v
  更新后D为：
```
[[1, 1, 1],[3, 2, 0],[3, 0, 0]
]
```
还原A（计算二维前缀和）：
- 行前缀和row_sum：
  第0行：[1,2,3]；第1行：[3,3+2=5,5+0=5]；第2行：[3,3+0=3,3+0=3]
- 列前缀和A：
  第0列：[1,4,7]；第1列：[2,2+5=7,7+3=10]；第2列：[3,3+5=8,8+3=11]
  得到更新后的A：
```
[[1, 2, 3],[4, 7, 8],[7, 10, 11]
]
```
可见(1,1)-(2,2)区域的元素5→7、6→8、8→10、9→11，均增加了2，符合预期。

五、代码实现

以下是二维差分分数组的构造、矩形更新、还原的完整C++代码：

#include <iostream>
#include <vector>
using namespace std;// 构造二维差分分数组（从A到D）
vector<vector<int>> init2DDiffArray(const vector<vector<int>>& A) {int n = A.size();if (n == 0) return {};int m = A[0].size();vector<vector<int>> D(n, vector<int>(m, 0));// 填充D[0][0]D[0][0] = A[0][0];// 填充第一行（i=0, j>0）for (int j = 1; j < m; ++j) {D[0][j] = A[0][j] - A[0][j-1];}// 填充第一列（j=0, i>0）for (int i = 1; i < n; ++i) {D[i][0] = A[i][0] - A[i-1][0];}// 填充非边界元素（i>0, j>0）for (int i = 1; i < n; ++i) {for (int j = 1; j < m; ++j) {D[i][j] = A[i][j] - A[i-1][j] - A[i][j-1] + A[i-1][j-1];}}return D;
}// 矩形区域更新：A[x1..x2][y1..y2] += v
void rectUpdate(vector<vector<int>>& D, int x1, int y1, int x2, int y2, int v) {int n = D.size();if (n == 0) return;int m = D[0].size();// 检查区间有效性if (x1 < 0 || x2 >= n || y1 < 0 || y2 >= m || x1 > x2 || y1 > y2) {cerr << "无效矩形区域！" << endl;return;}// 核心更新操作D[x1][y1] += v;if (y2 + 1 < m) {D[x1][y2 + 1] -= v;}if (x2 + 1 < n) {D[x2 + 1][y1] -= v;}if (x2 + 1 < n && y2 + 1 < m) {D[x2 + 1][y2 + 1] += v;}
}// 从二维差分分数组还原原数组（从D到A）
vector<vector<int>> restore2DArray(const vector<vector<int>>& D) {int n = D.size();if (n == 0) return {};int m = D[0].size();vector<vector<int>> A(n, vector<int>(m, 0));// 第一步：计算行前缀和vector<vector<int>> row_sum = D; // 复制D作为初始行前缀和for (int i = 0; i < n; ++i) {for (int j = 1; j < m; ++j) {row_sum[i][j] += row_sum[i][j-1];}}// 第二步：计算列前缀和（得到A）A[0] = row_sum[0]; // 第一行直接复制for (int i = 1; i < n; ++i) {for (int j = 0; j < m; ++j) {A[i][j] = A[i-1][j] + row_sum[i][j];}}return A;
}// 打印矩阵
void printMatrix(const vector<vector<int>>& mat, const string& name) {cout << name << ":\n";for (const auto& row : mat) {for (int num : row) {cout << num << "\t";}cout << "\n";}cout << endl;
}int main() {// 原数组A（3x3）vector<vector<int>> A = {{1, 2, 3},{4, 5, 6},{7, 8, 9}};printMatrix(A, "初始原数组A");// 构造二维差分分数组Dvector<vector<int>> D = init2DDiffArray(A);printMatrix(D, "初始差分分数组D");// 执行矩形更新：对(1,1)-(2,2)区域加2rectUpdate(D, 1, 1, 2, 2, 2);printMatrix(D, "更新后差分分数组D");// 还原原数组vector<vector<int>> newA = restore2DArray(D);printMatrix(newA, "更新后原数组A");return 0;
}

初始原数组A:
1       2       3       
4       5       6       
7       8       9       初始差分分数组D:
1       1       1       
3       0       0       
3       0       0       更新后差分分数组D:
1       1       1       
3       2       0       
3       0       0       更新后原数组A:
1       2       3       
4       7       8       
7       10      11

二维差分分数组通过记录二维前缀和的差值，将矩形区域更新优化为O(1)操作，其核心是理解“D的四个点更新如何控制A的前缀和范围”。构造D需基于原数组的边界和非边界元素分别计算，还原A则通过两次前缀和（行→列或列→行）实现。

与一维差分分数组类似，二维差分分数组适合离线场景（先积累所有更新，最后一次性还原），若需频繁中间查询，建议使用二维线段树等数据结构。

查看全文

http://www.dtcms.com/a/582637.html