当前位置： 首页 > news >正文

数据结构 -- 树（遍历）

news 2025/11/8 8:40:27

1、定义

在数据结构中，树的遍历是一种检查或更新树中节点值的过程。遍历树的方法主要分为两类：深度优先搜索（DFS）和广度优先搜索（BFS）。深度优先搜索包括前序遍历、中序遍历和后序遍历，而广度优先搜索通常指的是层次遍历。

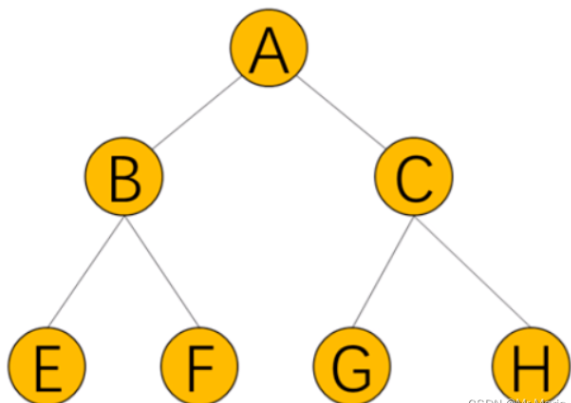
下面的例子均由该图为例：

2、深度优先搜索（DFS）

2.1 前序遍历（Pre-order Traversal）

前序遍历的顺序是先访问根节点，然后遍历左子树，最后遍历右子树。这种遍历方式可以使用递归实现，也可以使用栈来实现非递归版本。递归实现的代码结构简洁，易于理解，而非递归实现则需要利用栈来记录访问路径。

2.1.1 遍历结果：

A → B → E→ F→ C→ G→ H

2.1.2 核心代码：
// 前序遍历（根→左→右）
void preorder(TreeNode node, List<Integer> list) {if (node == null) return;list.add(node.val);      // 1. 先访问根preorder(node.left, list);  // 2. 再左子树preorder(node.right, list); // 3. 最后右子树
}
2.1.3 完整代码
  • 递归法：
import java.util.ArrayList;
import java.util.List;class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}
}public class BinaryTreePreorderTraversal {public static List<Character> preorderTraversal(TreeNode root) {List<Character> result = new ArrayList<>();preorder(root, result);return result;}private static void preorder(TreeNode node, List<Character> result) {if (node == null) {return;}result.add(node.val);       // 访问根节点preorder(node.left, result);  // 遍历左子树preorder(node.right, result); // 遍历右子树}public static void main(String[] args) {// 构建二叉树TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 前序遍历List<Character> traversalResult = preorderTraversal(root);System.out.println(traversalResult); // 输出: [A, B, E, F, C, G, H]}
}
  • 迭代法：
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}
}public class BinaryTreePreorderTraversal {public static List<Character> preorderTraversal(TreeNode root) {List<Character> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val); // 访问根节点// 注意：先压右子树，再压左子树（保证左子树先处理）if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return result;}public static void main(String[] args) {// 构建二叉树TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 前序遍历List<Character> traversalResult = preorderTraversal(root);System.out.println(traversalResult); // 输出: [A, B, E, F, C, G, H]}
}

2.2 中序遍历（In-order Traversal）

中序遍历首先遍历左子树，然后访问根节点，最后遍历右子树。这种遍历方法在二叉搜索树中特别有用，因为它可以按顺序访问所有节点。中序遍历同样可以递归实现，或者使用栈来实现非递归版本。

2.2.1 遍历结果：

E→ B→ F→ A→ G→ C→ H

2.2.2 核心代码：
// 中序遍历（左→根→右）
void preorder(TreeNode node, List<Integer> list) {if (node == null) return;preorder(node.left, list);  // 1. 先左子树list.add(node.val);      // 2. 在访问根preorder(node.right, list); // 3. 最后右子树
}
2.2.3 完整代码
  • 递归法
import java.util.ArrayList;
import java.util.List;public class BinaryTreeInorderTraversal {// 定义二叉树节点static class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}}// 递归实现中序遍历public static List<Character> inorderRecursive(TreeNode root) {List<Character> result = new ArrayList<>();inorder(root, result);return result;}private static void inorder(TreeNode node, List<Character> result) {if (node == null) {return;}inorder(node.left, result);   // 1. 递归遍历左子树result.add(node.val);         // 2. 访问根节点inorder(node.right, result);  // 3. 递归遍历右子树}public static void main(String[] args) {// 构造题目中的二叉树TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 调用递归中序遍历List<Character> resRecursive = inorderRecursive(root);System.out.println("递归中序遍历结果：" + resRecursive); // 输出：[E, B, F, A, G, C, H]}
}
  • 迭代法
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;public class BinaryTreeInorderTraversal {// 定义二叉树节点static class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}}// 迭代实现中序遍历public static List<Character> inorderIterative(TreeNode root) {List<Character> result = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {// 1. 一路向左，把所有左子节点压栈while (curr != null) {stack.push(curr);curr = curr.left;}// 2. 弹出栈顶，访问该节点curr = stack.pop();result.add(curr.val);// 3. 转向右子树，继续循环curr = curr.right;}return result;}public static void main(String[] args) {// 构造题目中的二叉树（同上）TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 调用迭代中序遍历List<Character> resIterative = inorderIterative(root);System.out.println("迭代中序遍历结果：" + resIterative); // 输出：[E, B, F, A, G, C, H]}
}

2.3 后序遍历（Post-order Traversal）

后序遍历先遍历左子树，然后遍历右子树，最后访问根节点。这种遍历方式常用于删除或释放树中的节点，因为它确保在删除节点之前先删除其所有后代节点。后序遍历也可以递归实现，或者使用两个栈来实现非递归版本。

2.3.1 遍历结果：

E→ F→  B→  G→  H→  C→  A

2.3.2 核心代码：
// 后序遍历（左→右→根）
void preorder(TreeNode node, List<Integer> list) {if (node == null) return;preorder(node.left, list);  // 1. 先左子树preorder(node.right, list); // 2. 再右子树list.add(node.val);      // 3. 最后访问根
}
2.3.3 完整代码：

  • 递归法
import java.util.ArrayList;
import java.util.List;public class BinaryTreePostorderTraversal {// 定义二叉树节点static class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}}// 递归实现后序遍历public static List<Character> postorderRecursive(TreeNode root) {List<Character> result = new ArrayList<>();postorder(root, result);return result;}private static void postorder(TreeNode node, List<Character> result) {if (node == null) {return;}postorder(node.left, result);   // 1. 递归遍历左子树postorder(node.right, result);  // 2. 递归遍历右子树result.add(node.val);         // 3. 访问根节点}public static void main(String[] args) {// 构造题目中的二叉树TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 调用递归后序遍历List<Character> resRecursive = postorderRecursive(root);System.out.println("递归后序遍历结果：" + resRecursive); // 输出：[E, F, B, G, H, C, A]}
}
  • 迭代法
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;public class BinaryTreePostorderTraversal {// 定义二叉树节点static class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}}// 迭代实现后序遍历public static List<Character> postorderIterative(TreeNode root) {List<Character> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();Stack<Boolean> visited = new Stack<>(); // 用于标记该节点是否已处理完左右子树stack.push(root);visited.push(false);while (!stack.isEmpty()) {TreeNode node = stack.peek();boolean isVisited = visited.peek();if (isVisited) {// 如果已经处理过左右子树，就弹出并访问result.add(stack.pop().val);visited.pop();} else {// 否则，标记为已处理，然后先把右、左子节点入栈（这样弹出时就是左→右）visited.pop();visited.push(true);// 先压右子树，再压左子树，保证左子树先被处理if (node.right != null) {stack.push(node.right);visited.push(false);}if (node.left != null) {stack.push(node.left);visited.push(false);}}}return result;}public static void main(String[] args) {// 构造题目中的二叉树（同上）TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 调用迭代后序遍历List<Character> resIterative = postorderIterative(root);System.out.println("迭代后序遍历结果：" + resIterative); // 输出：[E, F, B, G, H, C, A]}
}

3、广度优先搜索（BFS）

3.1 层次遍历（Level-order Traversal）

层次遍历从根节点开始，逐层从左到右遍历所有节点。这种遍历方式通常使用队列来实现，队列中存储着待访问的节点。层次遍历可以用来确定树的高度或者按层次打印树的节点。

3.1.1 遍历结果：

A → B → C → E → F → G → H​

3.1.2 核心代码：
// 核心层序遍历方法（返回 List<Character>）
public List<Character> levelOrder(TreeNode root) {List<Character> result = new ArrayList<>();if (root == null) return result;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);  // 1. 根节点入队while (!queue.isEmpty()) {TreeNode node = queue.poll();      // 2. 取出队首节点result.add(node.val);              // 3. 访问该节点（添加到结果）if (node.left != null) queue.offer(node.left);   // 4. 左子节点入队if (node.right != null) queue.offer(node.right); // 5. 右子节点入队}return result;
}
3.1.3 完整代码：（BFS + 队列，非递归）
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;// 定义二叉树节点
class TreeNode {char val;TreeNode left;TreeNode right;TreeNode(char val) {this.val = val;}
}public class SimpleLevelOrderTraversal {// 最简单的层序遍历方法（BFS，使用队列）public static List<Character> levelOrder(TreeNode root) {List<Character> result = new ArrayList<>();if (root == null) {return result;}// 使用队列辅助进行层次遍历Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);  // 根节点入队while (!queue.isEmpty()) {TreeNode node = queue.poll();  // 取出队首节点result.add(node.val);          // 访问该节点// 将左右子节点加入队列（如果存在）if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}return result;}public static void main(String[] args) {// 构建测试二叉树TreeNode root = new TreeNode('A');root.left = new TreeNode('B');root.right = new TreeNode('C');root.left.left = new TreeNode('E');root.left.right = new TreeNode('F');root.right.left = new TreeNode('G');root.right.right = new TreeNode('H');// 调用层序遍历List<Character> traversal = levelOrder(root);System.out.println(traversal);  // 输出: [A, B, C, E, F, G, H]}
}

4、遍历对比

遍历方式

顺序规则

实现方式

核心数据结构

前序遍历

根 → 左 → 右

DFS

递归栈​ / 显式栈​

中序遍历

左 → 根 → 右

DFS

递归栈​ / 显式栈​

后序遍历

左 → 右 → 根

DFS

递归栈​ / 显式栈 + 标记​

层次遍历

从上到下，从左到右

BFS

队列（Queue）

http://www.dtcms.com/a/581533.html

相关文章：

  • 浅析MySQL InnoDB存储引擎的MVCC实现原理
  • 手机传奇手游发布网站如何做网站做网站需要多少钱
  • ​TVS管选型设计：从理论到实践的全面解析-ASIM阿赛姆
  • 嵌入式开发中的“偷懒”艺术大纲
  • 网站开发期末作品代码和数据库运行好大全企业seo推广的绝密诀窍曝光
  • 石家庄企业网站网页设计wordpress主题demo
  • 宝塔 wordpress 多站点乐清营销网站
  • 【一、基础篇】Transformer 模型主要由哪两部分组成？
  • YASKAWA机器人焊机气体省气
  • Java--ACM常用语句
  • uniapp 微信小程序记录
  • Fastapi 进阶三：数据库的应用
  • 把VMware虚拟机下的Ubuntu系统文件夹中文路径名称改为英文（图文详解）
  • 建个小型网站服务器西部网站助手
  • How to manage python version via pyenv on mac m2 chip
  • 从零开始写算法-栈-最小值（记忆化pair)
  • 网站建设市场介绍电子商务网址
  • Sora：视频生成的突破与启示
  • Flutter：视频预览功能
  • IPIDEA海外代理助力-Youtube视频AI领域选题数据获取实践
  • 开机视频动画
  • 智能守护校园：视频汇聚平台EasyCVR如何构建校园消防安全新防线
  • 平台类网站建设企业网站个人备案
  • python+django/flask的车辆尾气检测排放系统-可视化大屏展示
  • AI Agent设计模式 Day 2：Plan-and-Execute模式：先规划后执行的智能策略
  • 32HAL——ADC模数转换多通道功能
  • 10_10_网站建站主页网站怎么建设
  • 模型不再是一整块！Hunyuan3D-Part 实现可控组件式 3D 生成
  • 【ZeroRange WebRTC】SDP 在 WebRTC 中的角色与工作原理（深入指南）
  • 高并发下的重复记录之谜：从前端到数据库的全方位排查