10.26-11.5力扣数组刷题

【1】34. 在排序数组中查找元素的第一个和最后一个位置

日期：10.26

1.题目链接：

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/?envType=problem-list-v2&envId=array2.类型：二分查找，数组

3.方法：二分查找（一次题解）

要找的就是数组中「第一个等于 target 的位置」（记为 leftIdx）和「第一个大于 target 的位置减一」（记为 rightIdx）。

二分查找中，寻找 leftIdx 即为在数组中寻找第一个大于等于 target 的下标，寻找 rightIdx 即为在数组中寻找第一个大于 target 的下标，然后将下标减一。两者的判断条件不同，为了代码的复用，定义 binarySearch(nums, target, lower) 表示在 nums 数组中二分查找 target 的位置，如果 lower 为 true，则查找第一个大于等于 target 的下标，否则查找第一个大于 target 的下标。

关键代码：

        int left=0,right=(int)nums.size()-1,ans=(int)nums.size();while(left<=right){int mid=(left+right)/2;if(nums[mid]>target||(lower && nums[mid]>=target)){right=mid-1;ans=mid;}else{left=mid+1;}}return ans;

【2】39. 组合总和

日期：10.27

1.题目链接：39. 组合总和 - 力扣（LeetCode）https://leetcode.cn/problems/combination-sum/description/?envType=problem-list-v2&envId=array2.类型：回溯，数组

3.方法：搜素回溯（半解）

定义递归函数 dfs(target,combine,idx) 表示当前在 candidates 数组的第 idx 位，还剩 target 要组合，已经组合的列表为 combine。递归的终止条件为 target≤0 或者 candidates 数组被全部用完。那么在当前的函数中，每次可以选择跳过不用第 idx 个数，即执dfs(target,combine,idx+1)。也可以选择使用第 idx 个数，即执行 dfs(target−candidates[idx],combine,idx)，注意到每个数字可以被无限制重复选取，因此搜索的下标仍为 idx。

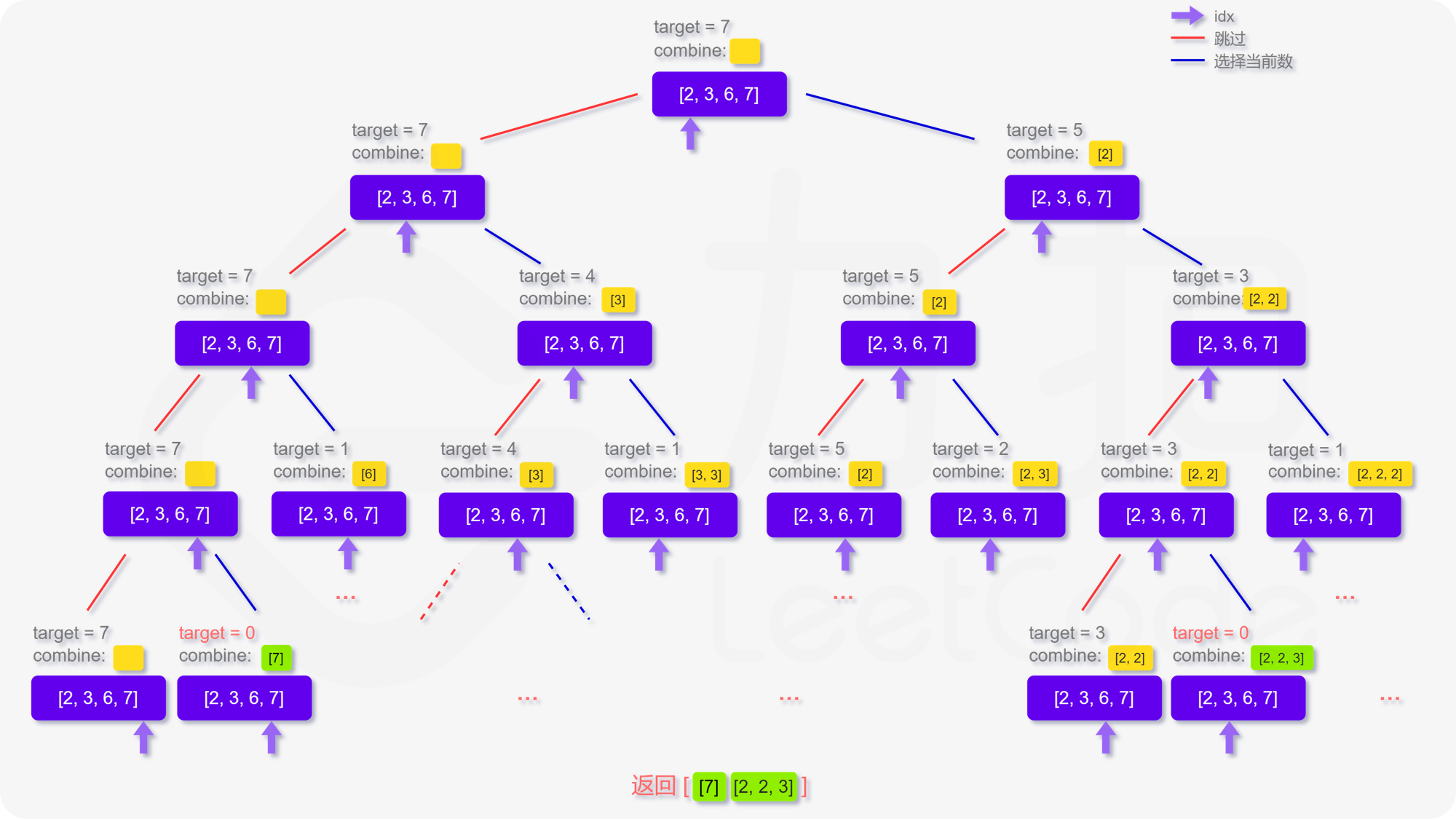
关键代码：

    void dfs(vector<int>& candidates,int target,vector<vector<int>>& ans,vector<int>& combine, int idx) {// 终止条件: 已经考虑完所有候选数字if(idx==candidates.size()){return;}        // 终止条件: 剩余目标值为0，找到有效组合if(target==0){ans.emplace_back(combine); return;}       // 分支1: 跳过当前数字，直接考虑下一个数字dfs(candidates,target,ans,combine, idx+1);     // 分支2: 选择当前数字if(target-candidates[idx]>=0){combine.emplace_back(candidates[idx]); // 目标值减去当前数字，索引不变dfs(candidates, target-candidates[idx], ans, combine, idx);combine.pop_back();  // 回溯}}

【3】40. 组合总和 II

日期：10.28

1.题目链接：40. 组合总和 II - 力扣（LeetCode）https://leetcode.cn/problems/combination-sum-ii/description/?envType=problem-list-v2&envId=array2.类型：回溯，数组

3.方法：回溯（半解）

使用一个哈希映射（HashMap）统计数组 candidates 中每个数出现的次数。在统计完成之后，将结果放入一个列表 freq 中，方便后续的递归使用。列表 freq 的长度即为数组 candidates 中不同数的个数。其中的每一项对应着哈希映射中的一个键值对，即某个数以及它出现的次数。
在递归时，对于当前的第 pos 个数，它的值为 freq[pos][0]，出现的次数为 freq[pos][1]，那么我们可以调用dfs(pos+1,rest−i×freq[pos][0])

关键代码：

        void dfs(int pos,int rest){// 终止条件: 剩余目标值为0，找到有效组合if(rest==0){ans.push_back(sequence);return;}// 终止条件: 已处理完所有数字或当前数字已大于剩余目标值if(pos==freq.size()||rest<freq[pos].first){return;}// 分支1: 跳过当前数字dfs(pos+1,rest);// 分支2: 选择当前数字1次到most次int most=min(rest/freq[pos].first, freq[pos].second);for(int i=1;i<=most;++i){sequence.push_back(freq[pos].first);  // 选择i次当前数字dfs(pos+1,rest-i*freq[pos].first);}// 回溯：移除刚才添加的所有当前数字for(int i=1;i<=most;++i){sequence.pop_back();}}

【4】49. 字母异位词分组

日期：10.29

1.题目链接：49. 字母异位词分组 - 力扣（LeetCode）https://leetcode.cn/problems/group-anagrams/description/?envType=problem-list-v2&envId=array2.类型：哈希表，排序，字符串，数组

3.方法：排序（一次题解）

由于互为字母异位词的两个字符串包含的字母相同，因此对两个字符串分别进行排序之后得到的字符串一定是相同的，故可以将排序之后的字符串作为哈希表的键。

关键代码：

        for(string& str: strs){string key=str;          sort(key.begin(), key.end()); // 对复制的字符串排序mp[key].emplace_back(str);  // 将原字符串添加到对应分组}       // 将哈希表中的分组提取到结果中vector<vector<string>> ans;for(auto it=mp.begin();it!= mp.end();++it){ans.emplace_back(it->second);  // 将每个分组加入结果}return ans;

【5】136. 只出现一次的数字

 日期：10.30

1.题目链接：136. 只出现一次的数字 - 力扣（LeetCode）https://leetcode.cn/problems/single-number/description/?envType=problem-list-v2&envId=array2.类型：哈希表，位运算，数组

3.方法：位运算（官方题解）

异或运算有以下三个性质。

任何数和 0 做异或运算，结果仍然是原来的数，即 a⊕0=a。
任何数和其自身做异或运算，结果是 0，即 a⊕a=0。
异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。

利用异或运算的性质：

出现两次的数字会相互抵消：a ^ a = 0

出现一次的数字会保留：a ^ 0 = a

关键代码：

        int ret=0;for(auto e: nums) ret^=e;return ret;

【6】80. 删除有序数组中的重复项 II

 日期：10.31

1.题目链接：80. 删除有序数组中的重复项 II - 力扣（LeetCode）https://leetcode.cn/problems/remove-duplicates-from-sorted-array-ii/description/?envType=problem-list-v2&envId=array2.类型：双指针，数组

3.方法：双指针（官方题解）

使用双指针技巧：

快指针 fast：遍历整个数组，检查每个元素

慢指针 slow：指向下一个有效元素应该写入的位置

核心逻辑：只有当当前元素 nums[fast] 与 nums[slow-2] 不相同时，才将其保留。这样可以确保任何元素在结果数组中最多出现两次。

关键代码：

        int n=nums.size();// 如果数组长度小于等于2，直接返回if(n<=2){return n;}// slow指向下一个要写入的位置，fast用于遍历数组int slow=2, fast=2;while (fast<n){// 检查当前元素是否可以保留if(nums[slow-2]!=nums[fast]){nums[slow]=nums[fast];  ++slow;                   // 移动慢指针}++fast;  // 移动快指针}return slow;  

【7】81. 搜索旋转排序数组 II

 日期：11.1

1.题目链接：81. 搜索旋转排序数组 II - 力扣（LeetCode）https://leetcode.cn/problems/search-in-rotated-sorted-array-ii/description/?envType=problem-list-v2&envId=array2.类型：二分查找，数组

3.方法：二分查找（半解）

这是对标准二分查找的改进，主要处理两个问题：

数组被旋转：数组不是完全有序的

存在重复元素：需要特殊处理重复的情况

关键代码：

            while(l<=r){int mid=(l+r)/2;            // 如果找到目标值，直接返回if(nums[mid]==target){return true;}           // 特殊情况：左、中、右三个值都相等if(nums[l]==nums[mid]&&nums[mid]==nums[r]){++l;--r;} // 左半部分有序else if(nums[l]<=nums[mid]){// 目标值在有序的左半部分if(nums[l]<=target&&target<nums[mid]){r=mid-1;}else{l=mid+1;}} // 右半部分有序else{// 目标值在有序的右半部分if(nums[mid]<target&&target<=nums[n-1]){l=mid+1;}else{r=mid-1;}}}

【8】128. 最长连续序列

 日期：11.2

1.题目链接：128. 最长连续序列 - 力扣（LeetCode）https://leetcode.cn/problems/longest-consecutive-sequence/description/?envType=problem-list-v2&envId=array2.类型：哈希表，数组

3.方法：哈希表（官方题解）

核心：一个连续序列完全由它的最小数字（起点）定义

算法步骤：

将所有数字存入哈希集合（去重 + O(1)查找）

对于每个数字，检查它是否是某个连续序列的起点

如果是起点，向后扩展计算序列长度

记录遇到的最大长度

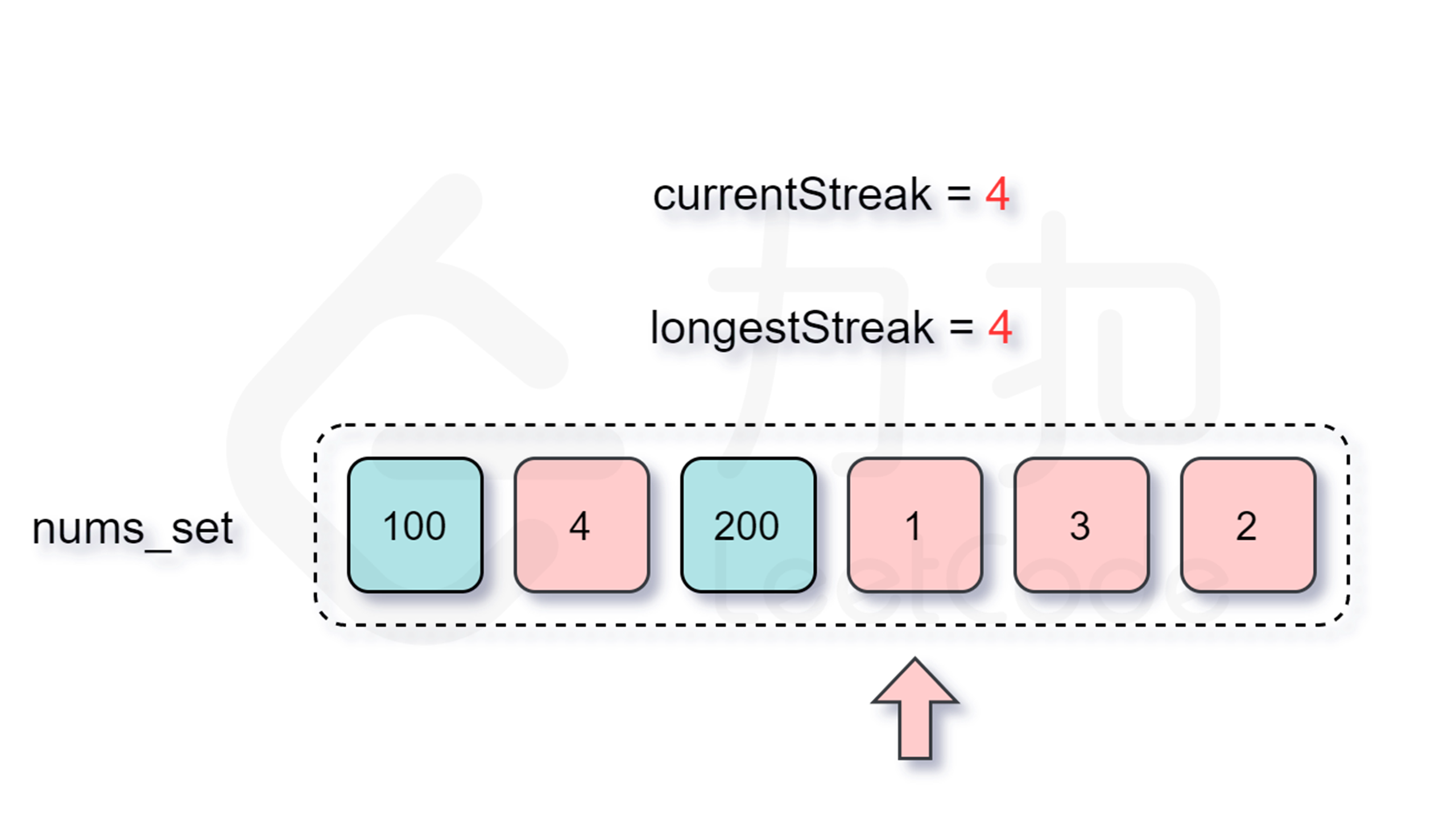
关键代码：

        unordered_set<int> num_set;for(const int& num : nums){num_set.insert(num);}int longestStreak=0; for(const int& num : num_set){// 只从序列的起点开始计算// 如果存在比当前数字小1的数字，说明当前数字不是序列起点if(!num_set.count(num-1)){int currentNum=num;int currentStreak=1;// 从起点开始，向后查找连续的数字while(num_set.count(currentNum+1)){currentNum+=1;currentStreak+=1;}// 更新最长序列长度longestStreak=max(longestStreak,currentStreak);}}

【9】134. 加油站

 日期：11.3

1.题目链接：134. 加油站 - 力扣（LeetCode）https://leetcode.cn/problems/gas-station/description/?envType=problem-list-v2&envId=array2.类型：贪心

3.方法：贪心（半解）

核心：如果从加油站 A 无法到达加油站 B，那么 A 和 B 之间的任何一个加油站都不能作为起点到达 B。

算法步骤：

从每个可能的起点开始尝试

模拟行驶过程，累计油量和消耗

如果在某个点油量不足，说明当前起点不可行

关键优化：当从起点 i 无法到达某个加油站 j 时，可以直接从 j+1 开始尝试，跳过中间的所有加油站

关键代码：

        while(i<n){int sumOfGas=0,sumOfCost=0;int cnt=0;           // 从当前起点i开始，尝试走完整个环形路线while(cnt<n){int j=(i+cnt)%n;  // 计算当前环形位置sumOfGas+=gas[j];sumOfCost+=cost[j];             // 如果累计消耗大于累计油量，无法继续前进if(sumOfCost>sumOfGas){break;}cnt++;}            // 如果成功走完了整个环形路线if(cnt==n){return i;}else{// 关键优化：跳过已经验证失败的区间i=i+cnt+1;}}

【10】152. 乘积最大子数组

 日期：11.4

1.题目链接：152. 乘积最大子数组 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-product-subarray/description/?envType=problem-list-v2&envId=array2.类型：动态规划

3.方法：动态规划（半解）

 状态转移方程

maxF = max(上一轮maxF * nums[i], max(nums[i], 上一轮minF * nums[i]))

minF = min(上一轮minF * nums[i], min(nums[i], 上一轮maxF * nums[i]))

对于每个新元素 nums[i]，以它结尾的最大乘积可能来自：

nums[i] 本身（重新开始）

maxF * nums[i]（延续之前的最大乘积）

minF * nums[i]（负数 × 负数 = 正数）

同样，最小乘积可能来自：

nums[i] 本身

minF * nums[i]（延续之前的最小乘积）

maxF * nums[i]（正数 × 负数 = 负数）

关键代码：

       for(int i=1;i<nums.size();++i){// 保存上一轮的值，因为计算新的maxF和minF时需要用到旧的maxF和minFlong mx=maxF,mn=minF;            // 更新以当前元素结尾的最大乘积maxF=max(mx*nums[i],max((long)nums[i],mn*nums[i]));// 更新以当前元素结尾的最小乘积minF=min(mn*nums[i],min((long)nums[i],mx*nums[i]));// 处理溢出情况if(minF<INT_MIN){minF=nums[i];}          ans=max(maxF, ans);}

【11】46. 全排列

 日期：11.5

1.题目链接：46. 全排列 - 力扣（LeetCode）https://leetcode.cn/problems/permutations/description/?envType=problem-list-v2&envId=array2.类型：动态规划

3.方法：动态规划（半解）

回溯的三要素

选择：swap(output[i], output[first])

递归：backtrack(res, output, first + 1, len)

撤销：swap(output[i], output[first])

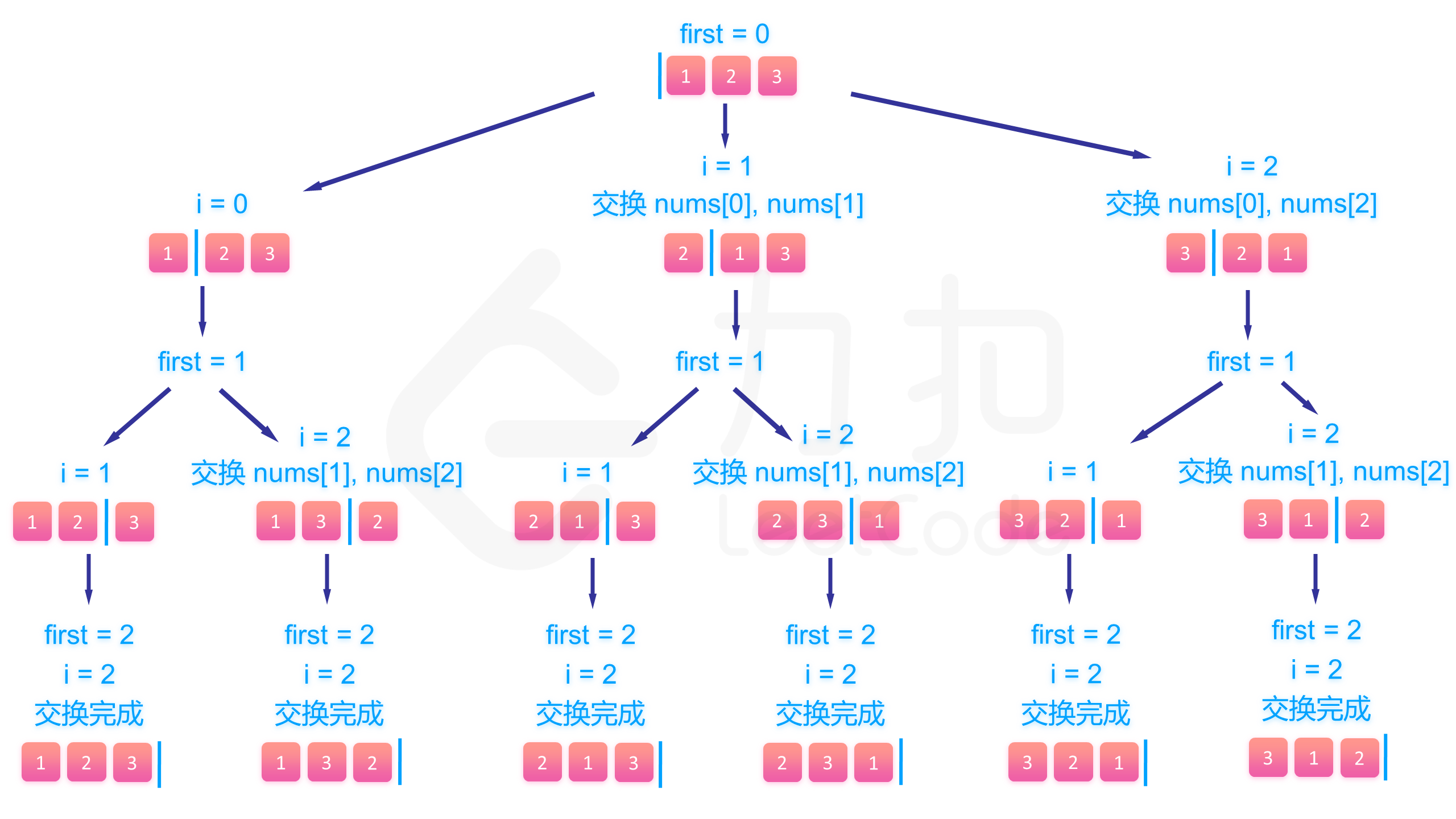
关键代码：

      if(first==len){res.emplace_back(output);  // 将当前排列加入结果集return;}// 遍历从first到len-1的所有位置for(int i=first;i<len;++i){// 动态维护数组：将第i个元素交换到first位置swap(output[i], output[first]);// 递归处理：固定first位置，处理first+1到len-1的位置backtrack(res, output, first + 1, len);// 撤销操作：恢复数组状态，进行回溯swap(output[i], output[first]);}