当前位置： 首页 > news >正文

数学分析简明教程——1.3

news 2025/10/31 13:36:37

【Easy】1.做出下列函数的图像

（4）y=sgn(sinx)

sgn(x)是一个符号函数，当x是正数时其值为1，反之为-1，当x为0时其值为0，图像如下

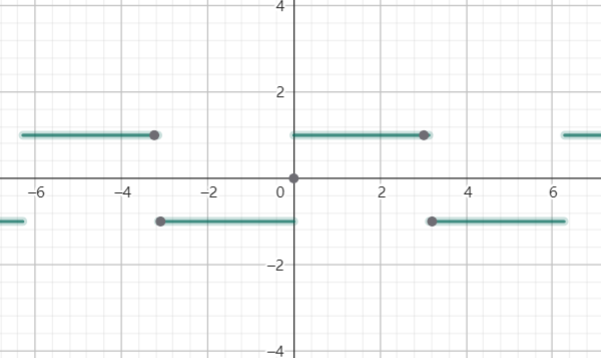
【Easy】2.比较函数图像，基本不会考

【Easy】3.根据图像1-4写出定义在[0,1]上的分段函数f_1(x)和f_2(x)的解析式表示式

【Easy】4.确定下列初等函数的存在域

(1)y=sin(sin(x)))  

sin(x)对定义域没有限制，所以D=(-\infty,+\infty).

(2)y=lg(lg(x))

lg(x)要求x大于0，即内部的lg(x)>0,所以D=(1,+\infty).

(3)y=arcsin(lg\frac{x}{10})

y=arcsin(x)的存在域是D=[-1,1]，故-1\leqslant lg(\frac{x}{10})\leqslant 1,D=[1,100].

(4)lg(arcsin(\frac{x}{10}))

lg(x)要求x大于0，即arcsin(\frac{x}{10})>0\rightarrow 0<\frac{x}{10}\leqslant 1,D=(0,10].

【Easy】5.设函数

f(x)=\left\{\begin{matrix}2+x,x\leqslant 0 \\\ 2^x,x>0 \end{matrix}\right.

求：(1)f(-3),f(0),f(1);(2)f(\Delta x)-f(0),(3)f(-\Delta x)-f(0)(\Delta x>0)

（2）f(\Delta x)-f(0)=2^{\Delta x}-2

（3）f(-\Delta x)-f(0)=2-\Delta x-2=-\Delta x

【Easy】6.设函数f(x)=\frac{1}{x+1}，求f(2+x),f(2x),f(x^2),f(f(x)),f(\frac{1}{f(x)})

f(f(x))=\frac{1}{1+\frac{1}{x+1}}=\frac{1+x}{2+x}

f(\frac{1}{f(x)})=\frac{1}{1+\frac{1}{f(x)}}=\frac{1}{2+x}

【Easy】7.试问下列函数是由哪些初等函数复合而成的

从里到外逐层分解即可，略

【Hard】8.在什么条件下，函数y=\frac{ax+b}{cx+d}的反函数就是其本身

补充：

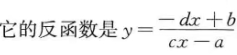这里有点跳跃，求解反函数可以通过交换xy

y=\frac{a}{c}+\frac{1}{c^2}\cdot \frac{bc-ad}{x+\frac{d}{c}}交换后x=\frac{a}{c}+\frac{1}{c^2}\cdot \frac{bc-ad}{y+\frac{d}{c}}\Rightarrow x-\frac{a}{c}=\frac{1}{c^2}\cdot \frac{bc-ad}{y+\frac{d}{c}}\Rightarrow y+\frac{d}{c}=\frac{1}{c^2}\cdot \frac{bc-ad}{x-\frac{a}{c}}

\Rightarrow y= \frac{bc-ad}{c^2x-ac}-\frac{d}{c}\Rightarrow y= \frac{bc-ad-\frac{d}{c}(c^2x-ac)}{c^2x-ac}\Rightarrow y= \frac{bc-acd-dcx+acd}{c^2x-ac}= \frac{b-dx}{cx-a}

由于反函数相等，故y= \frac{bc-acd-dcx+acd}{c^2x-ac}= \frac{b-dx}{cx-a}=\frac{ax+b}{cx+d}

(b-dx)(cx+d)=(ax+b)(cx-a)\Rightarrow bcx+bd-cdx^2-d^2x=acx^2-a^2x+bcx-ab\Rightarrow bd-cdx^2-d^2x=acx^2-a^2x-ab

为使x^2的系数相等，-cd=ac\Rightarrow a=-d

为使x的系数相等,a^2=d^2

故a+d=0

【Easy】9.试做出y=arcsin(sin(x))的图像

arcsinx的图像如图所示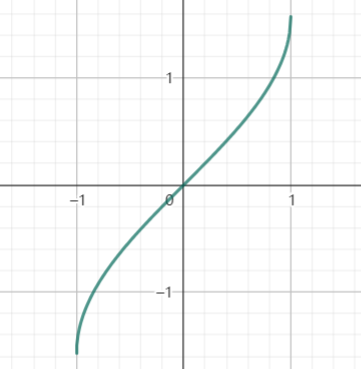

其定义域刚好是sinx的值域

内部的sinx与外部的反函数抵消得到下图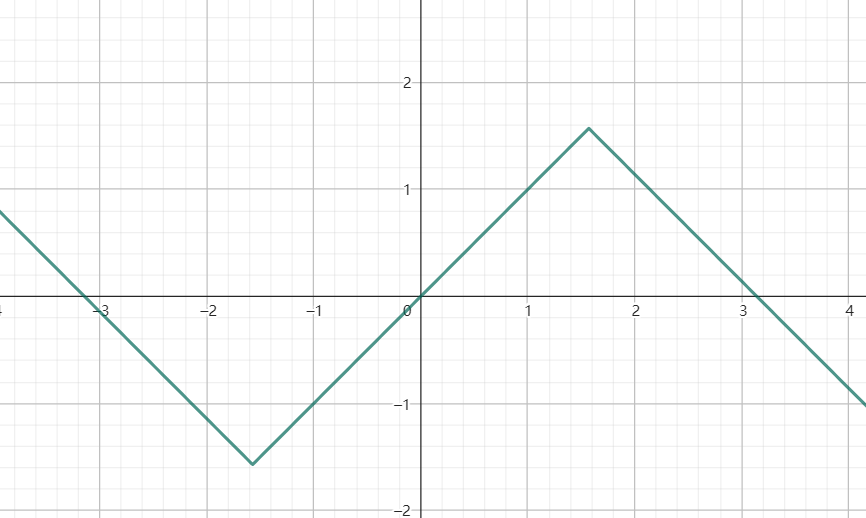

【Middle】10.试问下列等式是否成立

(1)tan(arctan(x))=x,x\in R

(2)arctan(tan(x))=x,x\in R

提示：arctan(x)的值域不是R所以(2)不成立

【Easy】11.试问y=|x|是初等函数吗

初等函数是由基本初等函数经过四则运算以及有限次复合而成的函数

y=|x|=\sqrt{x^2}，y=|x|是初等函数

【Middle】12.证明关于函数y=[x]的如下不等式：

（1）当x>0时，1-x<x[\frac{1}{x}]\leqslant 1

（2）当x<0时，1\leqslant x[\frac{1}{x}]< 1-x

由[x]的性质可知，x-1<[x]\leqslant x\Rightarrow \frac{1}{x}-1<[\frac{1}{x}]\leqslant \frac{1}{x}

当x>0时，左右同时乘以x，1-x<x[\frac{1}{x}]\leqslant 1

当x<0时，左右同时乘以x，1\leqslant x[\frac{1}{x}]< 1-x

http://www.dtcms.com/a/550421.html

相关文章：

  • 请将网站首页底部的备案号网站内容架构拓扑怎么做
  • Flutter---个人信息（2）---实现修改昵称
  • 深入解析 TCP 协议：从细节到实践的全方位解读
  • 题解：P12603 RuShiA（特殊情况下的 RSA 爆破）
  • 营销型网站建设和平台建设网站排行榜查询
  • 【代码】CF915E Physical Education Lessons [动态开点线段树]
  • 打造全新QAgent WeTest AI业务新上线
  • 虚拟主机怎么弄网站网站seo规范
  • 【技术经验】--如何和 Cursor 高效协作
  • 建网上商城的第三方网站哪个好17网站一起做网店潮汕
  • 關於概率部分，準備的三部曲
  • 新人做网站盈利北京小程序 app开发公司
  • 东莞网站设计智能 乐云践新网站开发 所有权
  • 在service方法中已经catch异常，Transactional失效怎么办
  • 服务平台网站设计门户网官网
  • 在线自助下单网站班级空间网站建设作用
  • Polarctf 写shell
  • 中建建筑网站机械设计师网课
  • 学习笔记一：基本术语
  • ssh网站开发的书籍织梦茶叶网站模板
  • 求网站建设详细过程网络规划设计师是高级职称吗
  • 【Linux权限 (二)】Linux权限机制深度解析：umask如何决定默认权限与粘滞位的妙用
  • 基于 Flask + APScheduler + MySQL 的自动报表系统设计
  • 建筑设计自学网站怎么开发一个自己的网站
  • go做网站网站建设优化东莞
  • AI智能座舱是什么？
  • 传奇手游网站大全9377网站建设哪便宜
  • 2023/12 JLPT听力原文 问题四
  • 域名备案时网站名称全国信息企业公示系统
  • Tokio的多线程调度器架构：深度解析与实践