rank(A+E) ＞= rank(A)证明

记录课堂证明：

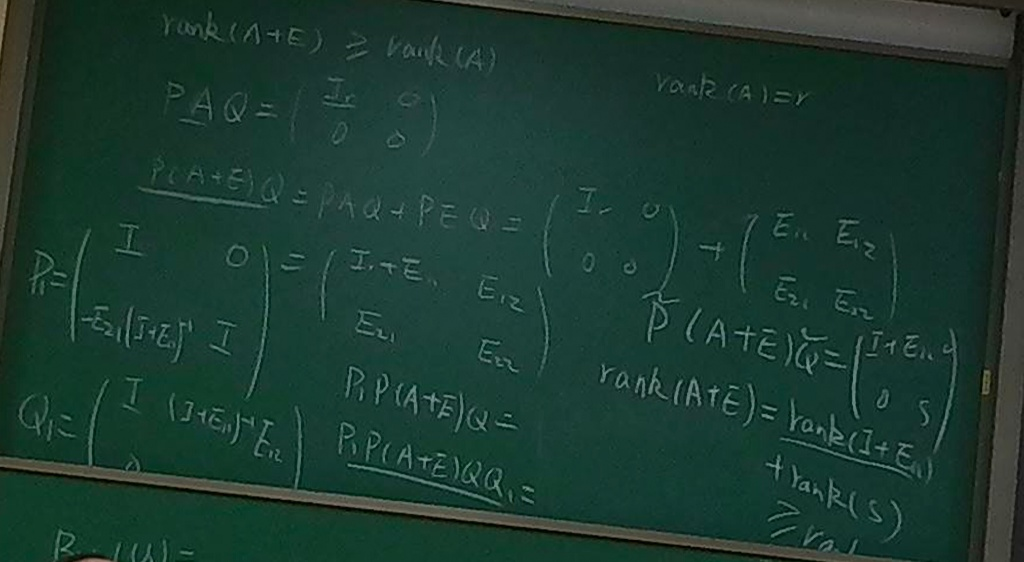
$\text{rank}(A+E)\ge \text{rank}(A)$ 并不是一个普遍成立的定理，而是在特定条件下才能成立。

这是一个非常经典和重要的特定情况。这个证明的核心是矩阵的等价变换（Equivalence Transformation）和舒尔补（Schur Complement）。

---

证明目标

给定一个矩阵 $A$ 和一个扰动矩阵 $E$，在某个特定条件下，$\text{rank}(A+E)\ge \text{rank}(A)$。

证明步骤详解

步骤一：对矩阵 A 进行"秩标准型"分解 (Rank Normal Form)

这是证明的起点。

1. 假设 $A$ 是一个 $m\times n$ 的矩阵，并且 $\text{rank}(A)=r$。（如黑板右上角所示）
2. 根据矩阵理论，任何矩阵 $A$ 都可以通过乘以可逆矩阵 $P$ (左乘) 和 $Q$ (右乘) 来"对角化"为它的"秩标准型"。
3. $PAQ=\left(\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right)$
   • $P$ 是一个 $m\times m$ 的可逆矩阵。
   • $Q$ 是一个 $n\times n$ 的可逆矩阵。
   • $I_r$ 是 $r\times r$ 的单位矩阵， $r$ 就是 $A$ 的秩。
   • $0$ 代表相应维度的零矩阵。

步骤二：将相同的变换应用于 (A+E)

这是整个证明最巧妙的地方。

1. 我们知道，用可逆矩阵去乘一个矩阵，不会改变它的秩。
2. 因此，$\text{rank}(A+E)$ 与 $\text{rank}(P(A+E)Q)$ 是相等的。
3. 黑板上展开了 $P(A+E)Q$：
   $$P(A+E)Q=P(AQ+EQ)=PAQ+PEQ$$
4. 现在，代入我们在步骤一中得到的 $PAQ$：
   $$P(A+E)Q=\left(\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right)+PEQ$$

步骤三：定义扰动矩阵的"分块"

1. 为了方便计算，我们将 $PEQ$ 这个"扰动"矩阵也按照 $PAQ$ 的分块方式进行分块。
2. 我们定义 $PEQ=\left(\begin{array}{cc}{E}_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right)$
   • 其中 $E_{11}$ 是一个 $r\times r$ 的矩阵（与 $I_r$ 维度相同）。
3. 将这个分块矩阵代入步骤二的末尾，我们得到 $P(A+E)Q$ 的完整形态：
   $$P(A+E)Q=\left(\begin{array}{cc}{I}_r+E_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right)$$

步骤四：最关键的一步 - 假设与分块消元

黑板上写出了 $P_1$ 和 $Q_1$ 两个矩阵，这是为了进行分块高斯消元。

1. 黑板上的隐含假设： 老师在写出 $P_1$ 和 $Q_1$ 时，用到了 $(I_r+E_{11}{)}^{-1}$ 这一项。这表明，此证明成立的前提条件（或特定条件）是：$(I_r+E_{11})$ 这个 $r\times r$ 矩阵是可逆的。

   • （在实际应用中，如果 $E$ 是一个"足够小"的扰动，那么 $I_r+E_{11}$ 就会"接近" $I_r$，从而保证可逆。所以这是一个关于小扰动的证明。）

2. 构造新的可逆矩阵 $P_1$ 和 $Q_1$ 来消去 $E_{12}$ 和 $E_{21}$：

   • $P_1=\left(\begin{array}{cc}I& 0\\ -E_{21}(I_r+E_{11}{)}^{-1}& I\end{array}\right)$
   • $Q_1=\left(\begin{array}{cc}I& -(I_r+E_{11}{)}^{-1}{E}_{12}\\ 0& I\end{array}\right)$
   • （注意： $P_1$ 和 $Q_1$ 都是可逆的，因为它们是对角线为 $I$ 的分块三角矩阵，行列式都为1。）

3. 因为 $P_1$ 和 $Q_1$ 可逆，我们再次使用 “乘以可逆矩阵不改变秩” 的性质：
   $$\text{rank}(A+E)=\text{rank}(P(A+E)Q)=\text{rank}(P_1[P(A+E)Q]Q_1)$$

4. 进行矩阵乘法：
   $$P_1[P(A+E)Q]Q_1=\left(\begin{array}{cc}I& 0\\ -E_{21}(I_r+E_{11}{)}^{-1}& I\end{array}\right)\left(\begin{array}{cc}{I}_r+E_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right)\left(\begin{array}{cc}I& -(I_r+E_{11}{)}^{-1}{E}_{12}\\ 0& I\end{array}\right)$$

   • 经过计算，这个复杂的乘法会"奇迹般"地消元，得到一个分块对角矩阵：
     $$=\left(\begin{array}{cc}{I}_r+E_{11}& 0\\ 0& S\end{array}\right)$$
   • 其中 $S=E_{22}-E_{21}(I_r+E_{11}{)}^{-1}{E}_{12}$。（这个 $S$ 就是著名的 $I_r+E_{11}$ 在 $P(A+E)Q$ 中的舒尔补 (Schur Complement)。）

步骤五：得出结论

现在我们得到了一个非常简洁的等式：
$$\text{rank}(A+E)=\text{rank}\left(\begin{array}{cc}{I}_r+E_{11}& 0\\ 0& S\end{array}\right)$$

1. 分块对角矩阵的秩等于其对角块的秩之和。
   $$\text{rank}(A+E)=\text{rank}(I_r+E_{11})+\text{rank}(S)$$

2. 根据我们在步骤四的关键假设，$(I_r+E_{11})$ 是一个 $r\times r$ 的可逆矩阵。

3. 可逆矩阵是满秩的，所以 $\text{rank}(I_r+E_{11})=r$。
   $$\text{rank}(A+E)=r+\text{rank}(S)$$

4. 矩阵的秩永远是非负的，即 $\text{rank}(S)\ge 0$。

5. 因此，$\text{rank}(A+E)\ge r$。

6. 最后，我们知道 $\text{rank}(A)=r$。

7. 证明完毕：$\text{rank}(A+E)\ge \text{rank}(A)$

总结

如果 $\text{rank}(A)=r$，并且存在可逆矩阵 $P,Q$ 使得 $PAQ$ 为秩标准型，那么对于一个扰动 $E$，只要 $A$ 的"有效部分"与 $E$ 的"有效部分"之和 $(I_r+(PEQ{)}_{11})$ 仍然是可逆的，那么 $A+E$ 的秩至少会保持 $A$ 的原秩 $r$。