2025-TMLR-Piecewise Constant Spectral Graph Neural Network
Information
- Authors: Vahan Martirosyan, Jhony H. Giraldo, Fragkiskos D. Malliaros
- Affiliations: Université Paris-Saclay
- 开源: https://github.com/vmart20/PieCoN
Abstract
- Existing Spectral GNNs:使用 low-degree polynomial filters 学习图谱域属性,由于阶数较低学到的信息有限,但是提高 degree 会带来额外的计算成本,且提升到一定程度后会出现 performance plateaus 甚至 degradation
- PieCoN: 将 constant spectral filters 和 polynomial filters 进行结合,通过对 spectrum 进行 adaptively partition,可以提高能学到的谱域属性的范围
1. Introduction
- Spatial GNNs 偏向 local structural information, Spectral GNNs 偏向 global structural patterns
- 现有 Spectral GNNs 使用 low-degree polynomial filters 的不足:
- 连续函数
- low degree 导致的无法对特定特征值赋以足够的权重——连续性导致的相邻特征值的权重无法急剧变化
- PieCoN;
- Cnstant filters:将特定范围的特征值和0值设为 1,将不同频段隔开,从而可以将重复次数过多的特征值的权重急剧降低,减少其对算法的影响
3. Background
- A^=UΛUT\hat A = U\Lambda U^TA^=UΛUT 为 A^=D−1/2AD−1/2\hat A = D^{-1/2}AD^{-1/2}A^=D−1/2AD−1/2的正交分解,sss 为不同的特征值的个数,v(λ)v(\lambda)v(λ)记录特征值重复出现的次数
4. Piecewise Constant Spectral GNN (PieCoN)
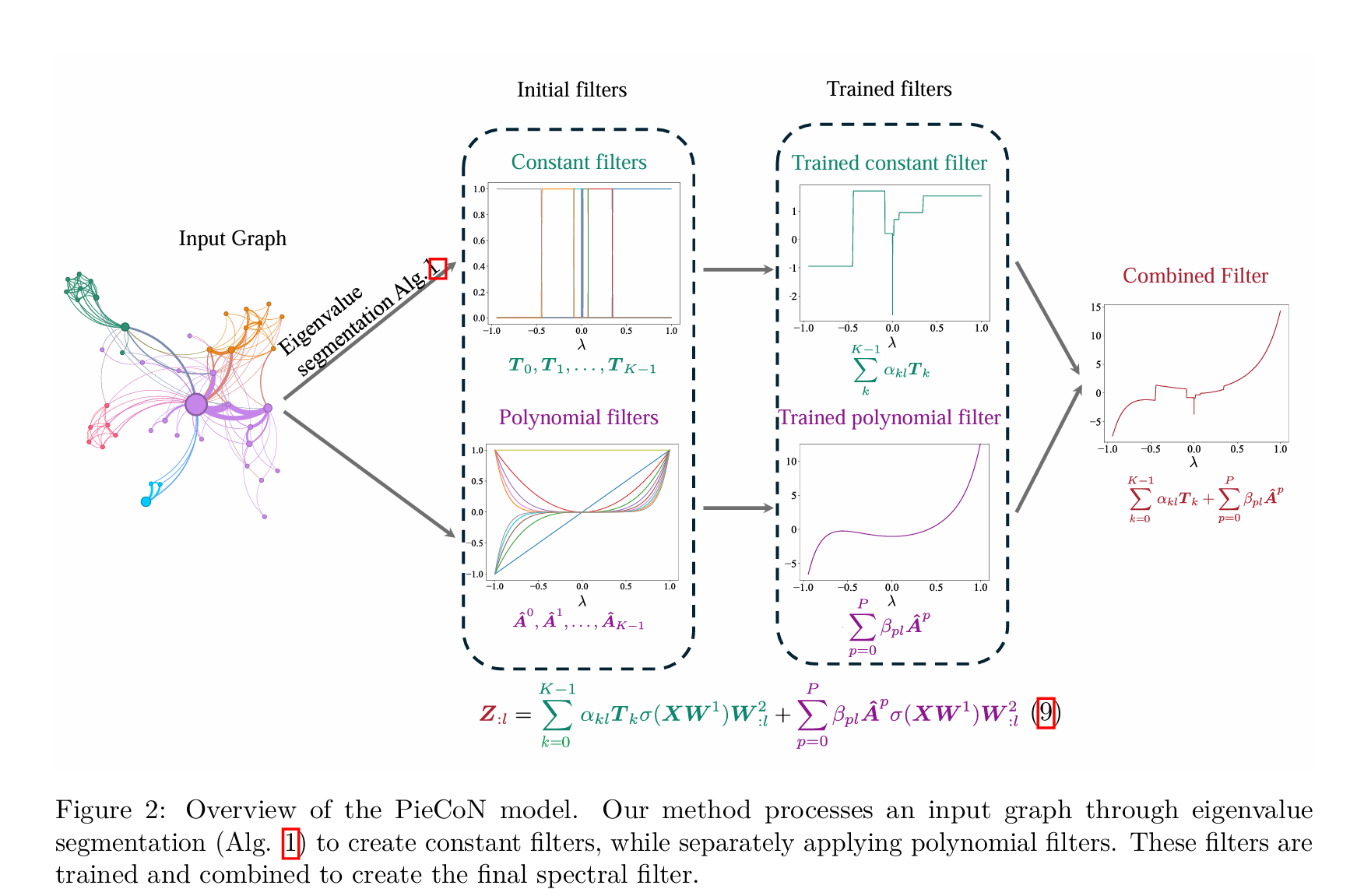
4.1 Identifying Significant Points in the Spectrum

- 通过判断某一特定特征值左右两侧大小为 www 的两个窗口内,特征值变化的趋势的大小判断特征值的重要程度:di−w:i={λi−w+1−λi−w,...,}d_{i-w:i}=\{\lambda_{i-w+1}-\lambda_{i-w},...,\}di−w:i={λi−w+1−λi−w,...,}
- 若存在一组相同的特征值,则重要性只记在第一次出现的特征值上,其他均记为0,以应对特征值重复带来的干扰
- 选出 K−2K-2K−2个最重要的特征值
- 最前面的和最后面的特征值怎么计算呢?
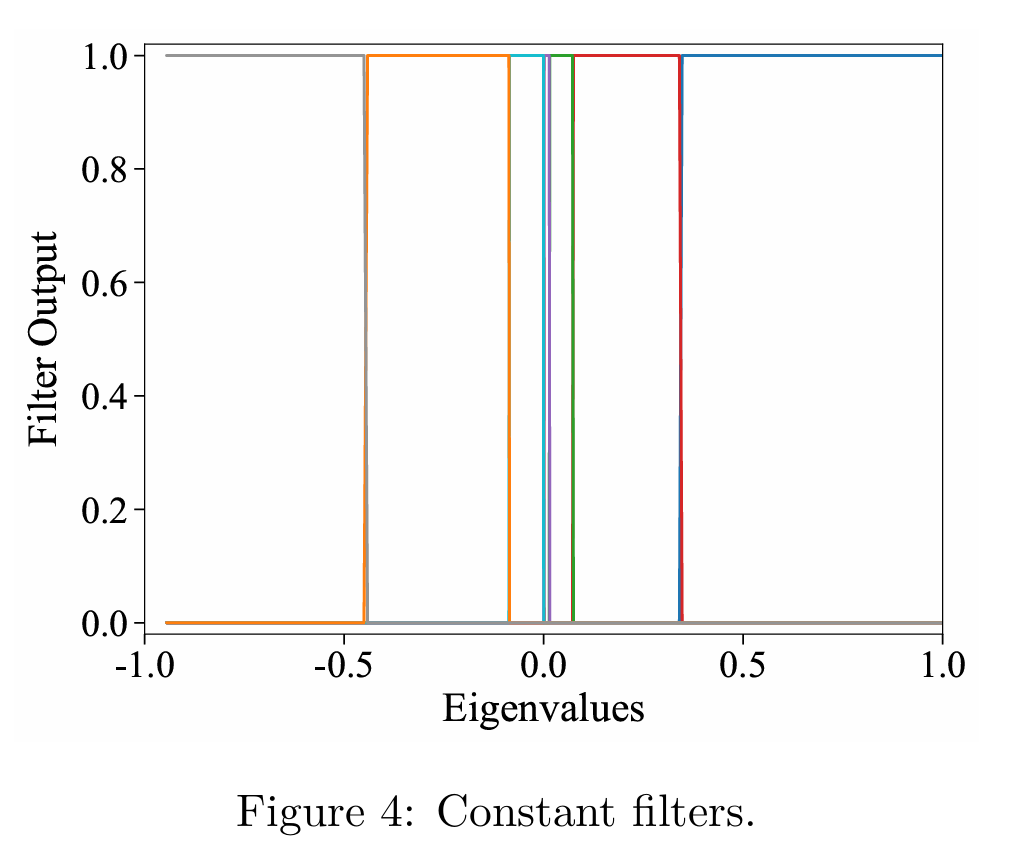
4.2 Construction of Constant Filters
- 对于频段 [ak,ak+1),Ek=diag(0,...,1,...,1...,0)[a_k,a_{k+1}),E_k=diag(0,...,1,...,1...,0)[ak,ak+1),Ek=diag(0,...,1,...,1...,0),即只有 aka_kak 到 ak+1−1a_{k+1}-1ak+1−1的部分不为0
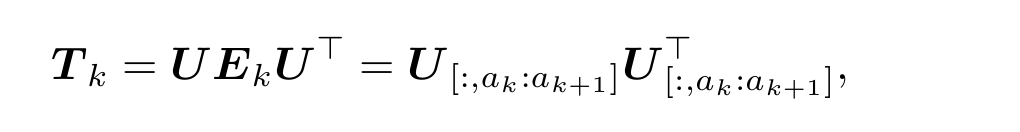
- 即设置了一个阶梯式的函数,在每个频段只有一个卷积核不为0,捕获频段信息
4.3 Polynomial Filters
和其他方法并无区别,用于捕获local neighborhood information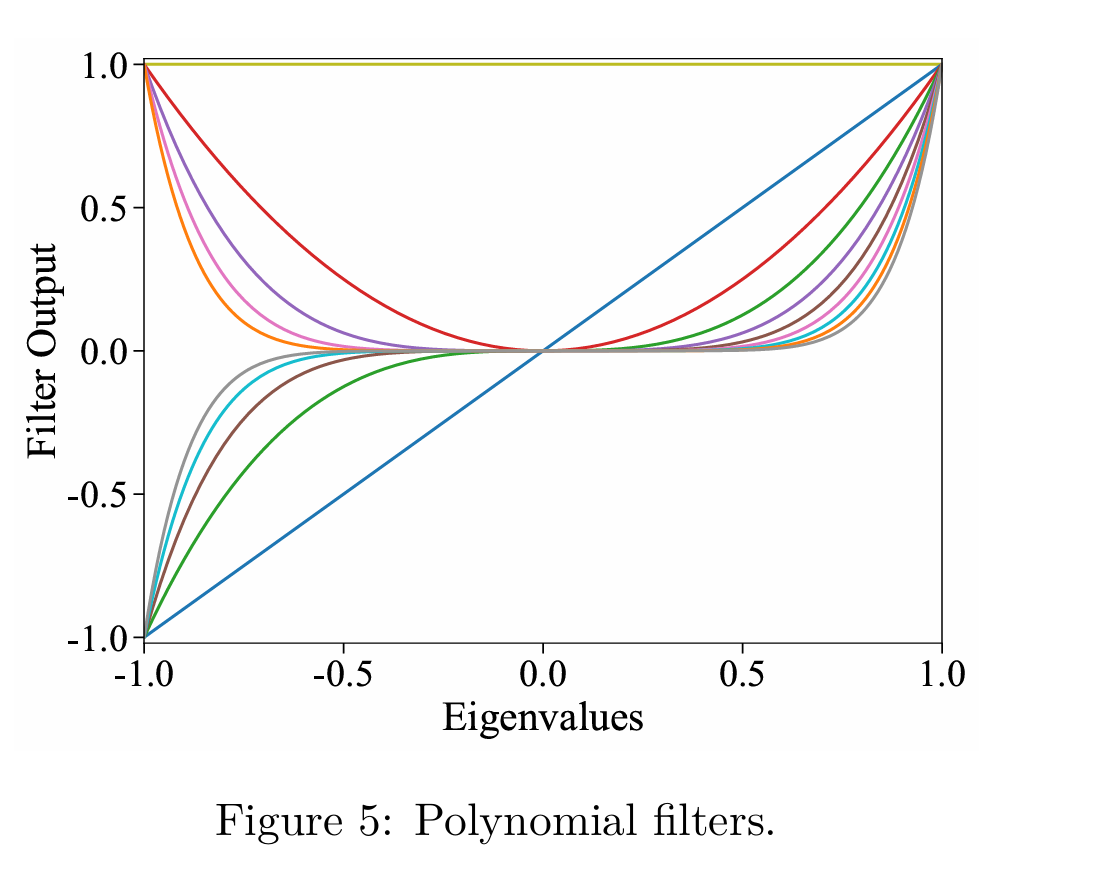
4.4 Combining Constant and Polynomial Filters
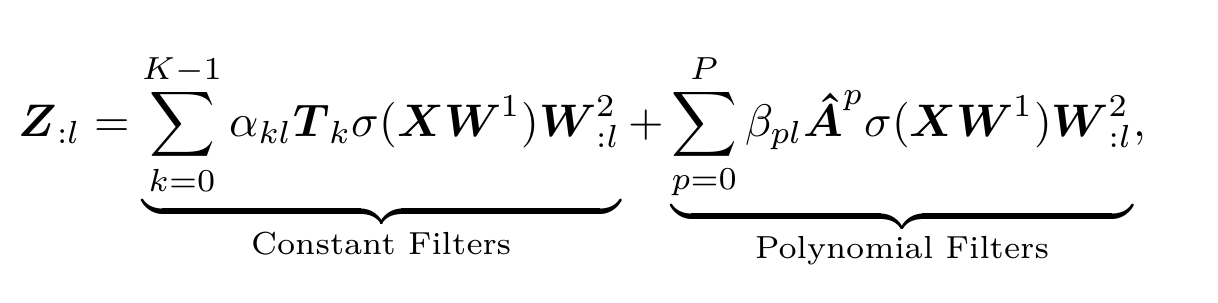
- TkT_kTk可以表示节点两两之间在当前频段上的相似度,令M=TkM=T_kM=Tk,则 MijM_{ij}Mij表示节点jjj对节点iii的重要程度,因此可以将MMM按正负区分开:
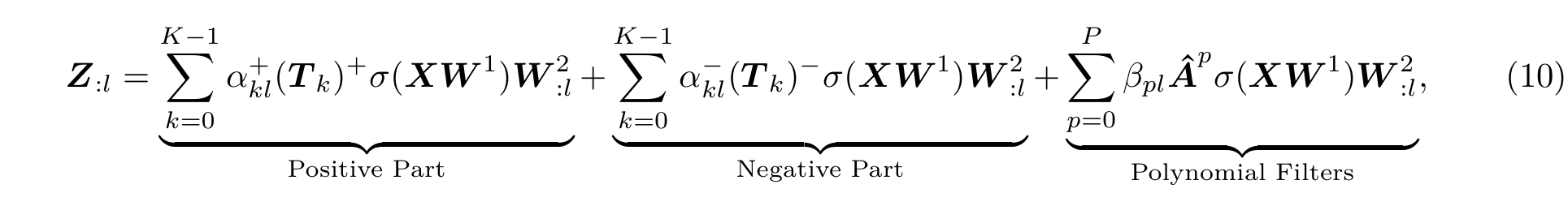
4.5 Computational Complexity
- Eigendecomposition(precomputation): O(n3))O(n^3))O(n3))
- Filter construction and sparsification(precomputation): O(n3+2Kn2log(m))=O(n3),mO(n^3+2Kn^2log(m))=O(n^3), mO(n3+2Kn2log(m))=O(n3),m为边的个数
- Model propagation: O((K+P)md)O((K+P)md)O((K+P)md)
5. Theoretical Analysis
5.1 Error Analysis for Polynomial Approximation
-
Approximation error for ϵ-dense eigenvalues: 证明了要用低次多项式精确近似滤波函数,多项式的范数不能太大,否则误差至少超过给出的下界
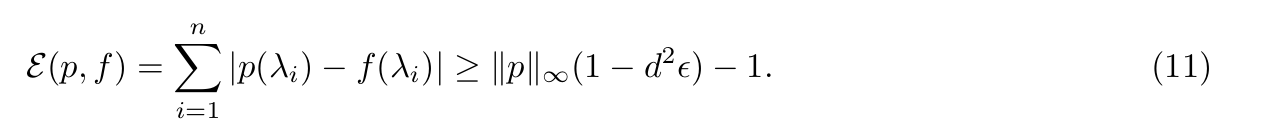
-
Approximation error for functions with jump discontinuities:
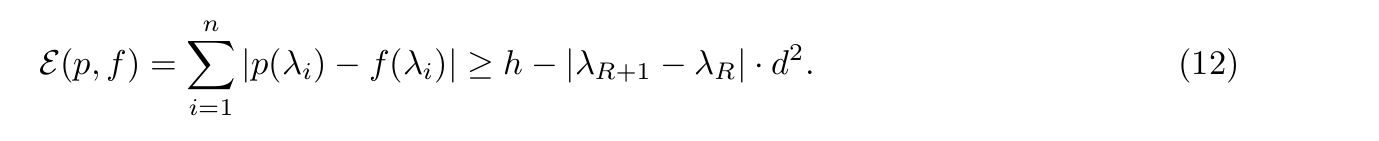
5.2 Sign and Basis Invariance
PieCoN 模型对特征向量的符号翻转和基变换具有不变性,这保证了模型在不同特征向量计算方法下的鲁棒性。
6. Experimental Evaluation
-
Datasets:
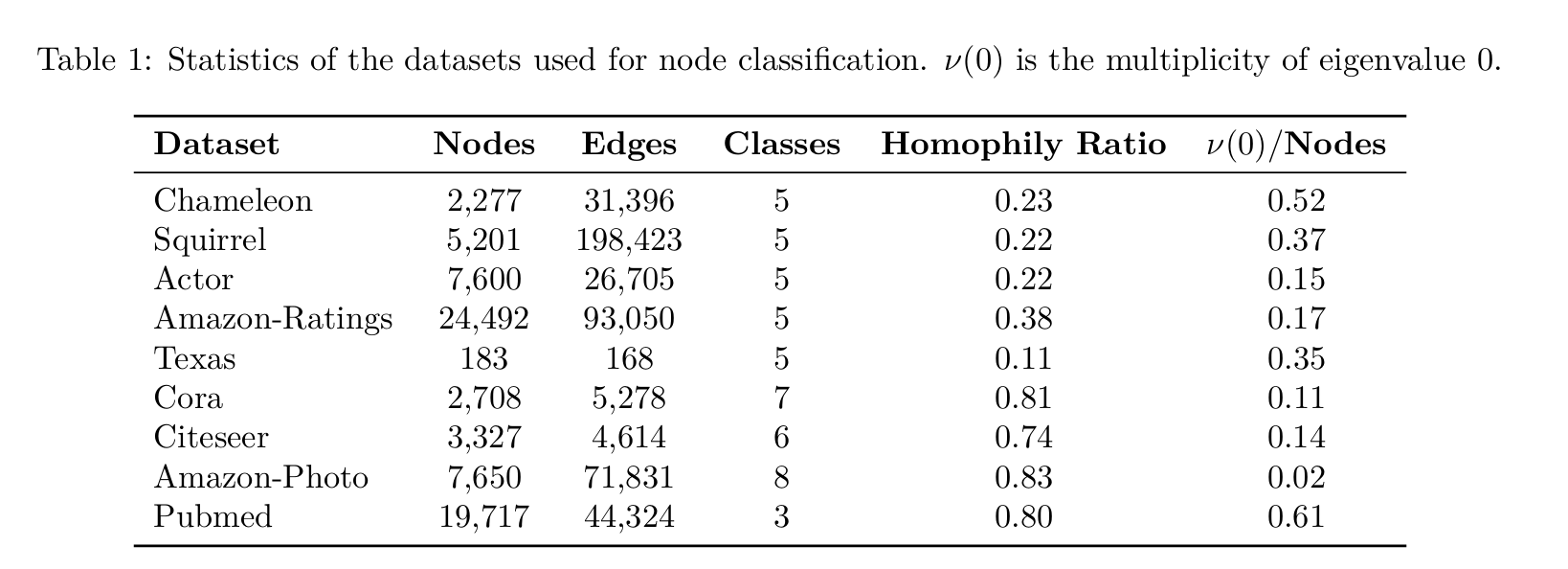
-
Results:
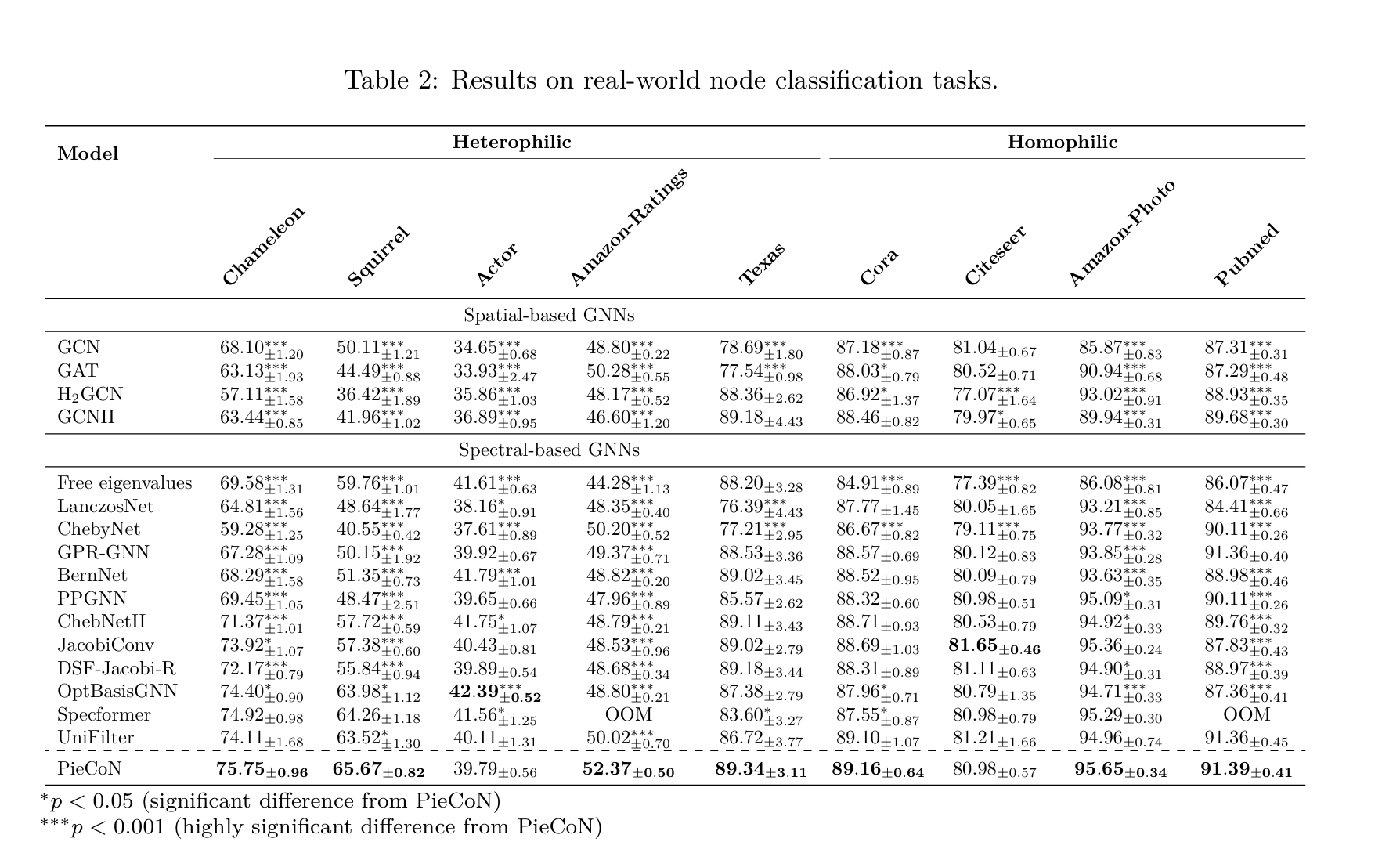
- 异构数据集上提升更高,可能和这些图的 normalized laplacian matrix 中存在大量重复的0值特征值有关
- 对于同构数据集表现尚可,没影响其对于 homophilic graphs 的能力
- 通过 t-tests 检验了提升效果的 statistical significance
- Free Eigenvalues 为将特征值都视为可训练参数,效果并不好,因为会丢失结构相关的信息
-
Ablation Study
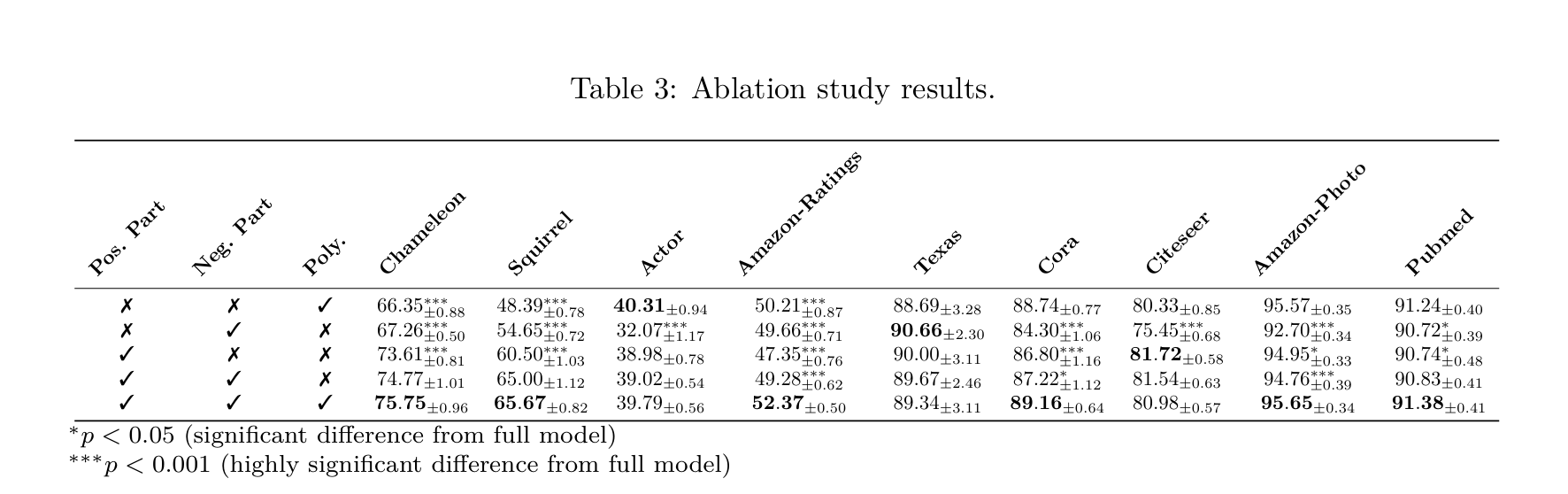
不同数据集上的表现差别还挺明显的 -
Limitations: 主要还是 O(n3)O(n^3)O(n3)的计算复杂度过高
