【算法】——动态规划之01背包问题

目录

一、什么是背包问题？

二、例题

1.【模板】01背包问题

2. 分隔等和子集

3. 目标和

4. 最后一块石头的重量Ⅱ

总结：

---

一、什么是背包问题？

给一个情景：

假如你现在有一个背包，地上有一堆物品，你可以挑选一些放入你的背包中。但你背包的空间大小是有限的，而不同的物品又有各自的不同体积和价值。

问：背包在有限的空间内选择的物品的最大价值是多少？

这种类型的问题就是背包问题，而背包问题又可以分为几类

根据物品存在的数量又可以分为3类：

1. 01背包问题，即每个物品只有一件，你可以选择拿(1)或不拿(0)

2. 完全背包问题，即每个物品有无数件，你可以重复拿同一物品

3. 多重背包问题，即每个物品有n件，每个物品的n不相同

另外，对背包的限制也能分为两类，一类是物品体积之和不超过背包的空间即可，还有一类是要求物品体积之和正好等于背包空间

今天我们要学习的就是01背包问题

二、例题

1.【模板】01背包问题

先看第一问：

状态表示：

首先根据题目要求和经验，我们初步可以定义dp[ i ]表示从前 i 个物品中选，所有选法中能选出来的最大价值。但当我们去推导状态时发现，从这个状态表示我们不知道背包此时的剩余空间状况，所以定义一维的dp表是不够的。

所以我们定义dp[ i ][ j ]表示，从前 i 个物品中挑选，总体积不超过 j 时，所有选法中能选出来的最大价值。

---

状态转移方程：

推导状态转移方程就涉及到两种情况，一种是没有选择第 i 个物品，此时直接等于dp[ i - 1][ j ]即可。另一种是选择了第 i 个物品，此时需要加上 i 物品的价值，并找到dp[ i - 1 ][ j - v[ i ] ]，另外，还要考虑 j - v[ i ]是否小于0，小于0会越界访问。 

综上，状态转移方程为：

如果 j >= v[i]，则dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);

否则就 dp[i][j] = dp[i-1][j];

---

初始化：

开辟空间时可以多出一行一列，第1个物品对应下标1，方便操作，初始化都初始化成0即可。

---

第二问：

第二问与第一问的区间就是要恰好装满背包，所以状态表示为：

定义dp[ i ][ j ]表示，从前 i 个物品中挑选，总体积正好等于 j 时，所有选法中能选出来的最大价值

状态转移方程变为：

如果 j >= v[i] && dp[i-1][j-v[i]] != -1，则dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);

否则就 dp[i][j] = dp[i-1][j];

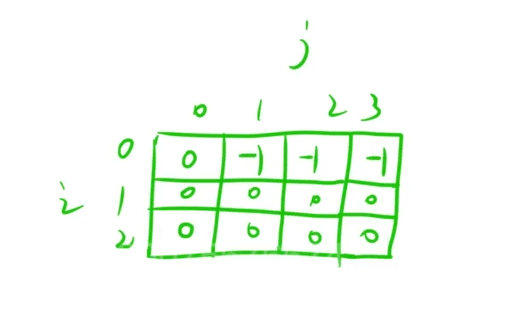
初始化时，由于要求正好装满，所以第一列除了第一个外都要初始化为-1（约定如果不存在刚好装满的情况就赋值-1）

示例代码：

#include <iostream>
using namespace std;//n的最大规模是1000，所以直接定义一个最大值，便于操作
const int N = 1001;
int n, V;// 物品数量与容量
int v[N], w[N];// 物品的体积与价值
int dp[N][N];int main() {cin>>n>>V;// 浪费一个空间来达成条件对称，第1个物品对应下标1for(int i = 1; i <= n; i++){cin>>v[i];cin>>w[i];}// 第一问// 默认都是0，无需初始化for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){if(j >= v[i]){dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);}else{dp[i][j] = dp[i-1][j];}}}cout<<dp[n][V]<<endl;// 第二问，复用一下第一问的dp表// 初始化，第一行除了第一个都初始化为-1for(int j = 1; j <= V; j++){dp[0][j] = -1;}for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){if(j >= v[i] && dp[i-1][j-v[i]] != -1){dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);}else{dp[i][j] = dp[i-1][j];}}}cout<<(dp[n][V] != -1 ? dp[n][V] : 0)<<endl;return 0;
}

1. 代码题为了方面，我们直接建1001大小的数组

2. 第二问输出时要处理结构为-1的情况，使其输出0

利用滚动数组进行优化

由上题的状态转移方程可知，求dp[ i ][ j ]时只用到了dp[ i - 1 ]这一列，所以之前的数据都可以舍弃掉。又当 j >= v[i]时，dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])，发现dp[i][j]的值和dp[i-1][j-v[i]]的值有关，是将前面的值赋值给后面，所以我们改变一下策略，只用一个数组，并改为从后往前遍历，这样就能刚好能用到i-1行的值。

可以拿出状态转移遍历的一段代码，看一下前后代码的区别：

修改前

for(int i = 1; i <= n; i++){for(int j = 1; j <= V; j++){if(j >= v[i]){dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i]);}else{dp[i][j] = dp[i-1][j];}}}

修改后

for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){dp[j] = max(dp[j], dp[j-v[i]] + w[i]);}}

优化后完整代码：

#include <iostream>
using namespace std;//n的最大规模是1000，所以直接定义一个最大值，便于操作
const int N = 1001;
int n, V;// 物品数量与容量
int v[N], w[N];// 物品的体积与价值
int dp[N];int main() {cin>>n>>V;// 浪费一个空间来达成条件对称，第1个物品对应下标1for(int i = 1; i <= n; i++){cin>>v[i];cin>>w[i];}// 第一问// 默认都是0，无需初始化for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){dp[j] = max(dp[j], dp[j-v[i]] + w[i]);}}cout<<dp[V]<<endl;// 第二问，复用一下第一问的dp表// 初始化，第一行除了第一个都初始化为-1for(int j = 1; j <= V; j++){dp[j] = -1;}for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){if(dp[j-v[i]] != -1){dp[j] = max(dp[j], dp[j-v[i]] + w[i]);}}}cout<<(dp[V] != -1 ? dp[V] : 0)<<endl;return 0;
}

2. 分隔等和子集

这道题初看感觉和背包问题没什么关系，但不急，我们分析看看。题目要求将数组分隔成两个子集，并且两个子集的元素和相等，那也就相当于是在数组中选出若干个元素，使得选出的元素和等于总元素和的一半。这就类似于背包问题中选择若干个物品，使其体积正好等于sum/2，并且还比上一道模板背包问题少了价值最大这一条件。

所以，状态表示可以为，dp[i][j]表示，在前 i 个元素中，是否存在一种选法，使其元素和等于 j ，存在则值为1，不存在则值为0

状态转移方程要分两种情况，一种是没选第 i 个元素，此时与前一个状态有关，dp[i][j] = dp[i-1][j]， 第二种是选择了第 i 个元素，此时要加上当前元素的值，相当于去找元素和等于sum/2 - 当前元素值的情况存不存在，所以dp[i][j] = dp[i-1][j-nums[i-1]](因为初始化多开了一行一列，所以与nums数组对应时要-1)

综上，状态转移方程为：dp[i][j] = (dp[i-1][j] || dp[i-1][j-nums[i-1]])，两种情况取或||

初始化可以多创建一行一列，第一列是表示元素和等于0，只要不选就行，所以初始化为true

示例代码：

class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size();int sum = 0;for(auto e : nums){sum += e;}// 如果元素和不能等分就直接返回falseif(sum%2 == 1){return false;}int target = sum/2;vector<vector<bool>> dp(n+1, vector<bool>(target+1));//初始化for(int i = 0; i <= n; i++){dp[i][0] = true;}for(int i = 1; i <= n; i++){for(int j = 1; j <= target; j++){if(j >= nums[i-1]){dp[i][j] = (dp[i-1][j] || dp[i-1][j-nums[i-1]]);}else{dp[i][j] = dp[i-1][j];}}}return dp[n][target];}
};

使用滚动数组优化方案：

class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size();int sum = 0;for(auto e : nums){sum += e;}// 如果元素和不能等分就直接返回falseif(sum%2 == 1){return false;}int target = sum/2;vector<bool> dp(target+1);//初始化dp[0] = true;for(int i = 1; i <= n; i++){for(int j = target; j >= nums[i-1]; j--){dp[j] = (dp[j] || dp[j-nums[i-1]]);}}return dp[target];}
};

3. 目标和

这道题也是，需要分析一下才能转化为01背包问题，将数组中的数据添加正负，然后串联后得到target，也就是说数组中一部分数据为正，一部分数据为负，假定设为正的数据和为a，设为负的数据和为b，所以a - b = target，又a + b = sum，所以可以推出a = (target + sum)/2。所以题目转化为在数组中选出若干数据，使其相加等于(target + sum)/2

状态表示：dp[i][j]表示为前 i 个数据选择数据，数据之和恰好为 j 的选法数目

状态转移方程：

dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]]（有选/不选第i个元素两种情况，选法数相加）

示例代码：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size();int sum = 0;for(auto e : nums){sum += e;}int aim = (sum + target)/2;if(aim < 0 || (sum + target)%2){return 0;}vector<vector<int>> dp(n+1, vector<int>(aim+1));for(int i = 0; i <= n; i++){dp[i][0] = 1;}for(int i = 1; i <= n; i++){for(int j = 0; j <= aim; j++){dp[i][j] = dp[i-1][j];if(j >= nums[i-1]){dp[i][j] += dp[i-1][j-nums[i-1]];}}}return dp[n][aim];}
};

滚动数组优化后代码：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int n = nums.size();int sum = 0;for(auto e : nums){sum += e;}int aim = (sum + target)/2;if(aim < 0 || (sum + target)%2){return 0;}vector<int> dp(aim+1);dp[0] = 1;for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i-1]; j--){dp[j] += dp[j-nums[i-1]];}}return dp[aim];}
};

4. 最后一块石头的重量Ⅱ

分析：

要将石头粉碎，最后得到一块最小的石头，本质还是一部分设为正数，一部分设为负数，并且让正数和负数的绝对值尽可能地接近，此时就能得到最小值。那么我们可以先求出整个数组的和sum，然后从数组中选出部分数据，使数据和尽可能接近sum/2

状态表示：dp[i][j]表示从前 i 个数据中选，数据和不超过 j 时，数据和的最大值

状态转移方程要分选/不选第 i 个数据，两种情况取最大值

dp[i][j] = max(dp[i-1][j]，dp[i-1][j-stones[i]]+stones[i-1])（前提是j>stones[i]，否则就直接等于dp[i-1][j]）

初始化默认都是0，无需初始化

示例代码：

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size();int sum = 0;for(auto e : stones){sum += e;}int target = sum/2;vector<vector<int>> dp(n+1, vector<int>(target+1));for(int i = 1; i <= n; i++){for(int j = 1; j <= target; j++){dp[i][j] = dp[i-1][j];if(j >= stones[i-1] ){dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i-1]]+stones[i-1]);}}}return sum - 2*dp[n][target];}
};

注意返回值有所不同

滚动数组优化后代码：

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int n = stones.size();int sum = 0;for(auto e : stones){sum += e;}int target = sum/2;vector<int> dp(target+1);for(int i = 1; i <= n; i++){for(int j = target; j >= stones[i-1]; j--){dp[j] = max(dp[j], dp[j-stones[i-1]]+stones[i-1]);}}return sum - 2*dp[target];}
};

总结：

本文介绍了背包问题并重点学习了01背包问题。第一道例题是模板题，通过这道题我们可以了解01背包问题的解决问题的通用方法。

后续几道题都是衍生出来的例题，需要先进行一定的转化才能变为01背包问题。关于如何转化，我们只需抓住01背包问题最核心的点，即在一组数据中选or不选第 i 个数据，然后能得到我们想要的成果

以上便是本文的所有内容了，如果觉得有帮助的话可以点赞收藏加关注支持一下！