SR-Scientist: 利用 ai agent 进行科学公式的发现

Abstract 

近年来，大语言模型（LLM）已被应用于科学方程发现领域，利用其内嵌的科学知识来生成假设。然而，现有方法通常将 LLM 局限于搜索算法（如遗传规划）中的“方程提议者”角色。本文提出了一种新的框架——SR-Scientist，它将 LLM 从一个简单的方程提议者提升为一个自主的 AI 科学家，能够编写代码进行数据分析、将方程实现为代码、提交结果进行评估，并根据实验反馈不断优化方程。具体而言，我们将代码解释器封装为一组工具，用于数据分析和方程评估。该智能体在最少人工定义流程的情况下，通过使用这些工具进行长程优化。实验结果表明，SR-Scientist 在涵盖四个科学学科的数据集上，比基线方法的表现高出 6% 至 35%。此外，我们验证了该方法在噪声环境下的鲁棒性、在跨领域数据上的泛化能力以及在符号层面的准确性。最后，我们还开发了一个端到端的强化学习框架，以进一步增强智能体的能力。

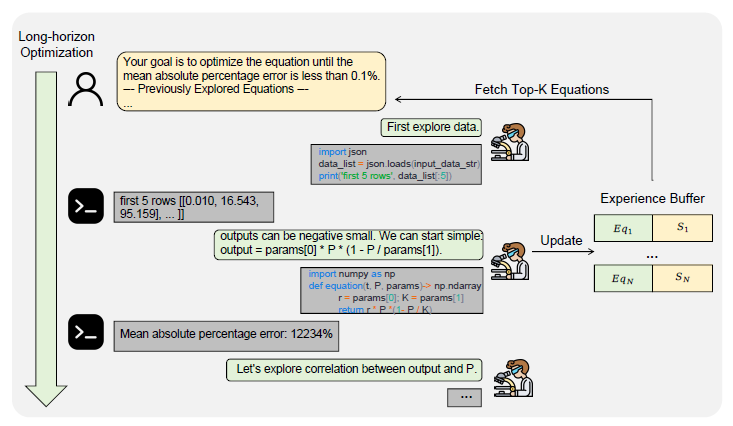
Figure1: SR-Scientist的推理框架。在每次迭代中，LLM代理使用代码解释器自主进行长期优化，进行数据分析和方程评估。为了克服当前llm的上下文长度限制，我们实现了一个 经验缓冲区experience buffer 来获取后续迭代中表现最好的方程。“Eq”表示方程，“S”表示方程得分。

Contribution

•  我们开发了名为 SR-Scientist 的框架，该框架中一个自主智能体通过长期视角 long-horizon、工具驱动的数据分析 tool-driven data analysis 以及方程评估equation evaluation来发现科学方程式。
•  我们证明，SR-Scientist 在精度、泛化能力、对噪声的鲁棒性以及符号准确性方面显著优于基线方法。 
•  我们还开发了一个相应的端到端强化学习流程，以增强智能体的能力。

Related Work

Symbolic Regression

目标: 从数据中自动发现表达变量关系的数学方程，而不是像普通回归那样只输出一个数值模型。 (Cava et al., 2021; Makke and Chawla, 2024). 

Current popular methods can be categorized as follows:

1) GP(genetic programming)-based Methods: This line of methods uses constrained representations, such as expression trees, to define a search space composed of symbolic operators, constants, and variables (Cranmer, 2023). Evolutionary or genetic programming is then applied to search for solutions.

2) Deep learning Methods: These methods leverage deep neural networks to learn a direct mapping from numerical observations to their underlying mathematical expressions through online (Landajuela et al., 2022; Petersen et al., 2021) or offline learning (Biggio et al., 2021; Kamienny et al., 2022).

	Online Learning（在线学习）	Offline Learning（离线学习）
	模型在与环境交互时实时接收数据并更新参数	模型在固定数据集上进行一次性训练

3) LLM-based methods: Due to the efficiency and scalability issues of the above methods, the research community has integrated LLMs with traditional techniques like GP, leveraging the models’ extensive knowledge to generate more informed hypotheses (Grayeli et al., 2024; Ma et al., 2024; Shojaee et al., 2024; Wang et al., 2025b). While promising, current hybrid methods still lack the direct analysis of observed data through tools to gain insights. Furthermore, the LLM’s behavior is often fixed, lacking the autonomy to decide its actions in a goal-oriented manner. Moreover, most work focuses on using LLMs for inference, without exploring how these models evolve their abilities through methods like RL.

Agentic AI

Agentic AI can autonomously execute complex tasks in dynamic environments requiring adaptation, interaction, and reasoning in a goal-oriented manner (Schneider, 2025). However, there has been limited focus on scientific discovery. In this paper, we demonstrate that with careful design, these agentic models can be powerful for equation discovery and can also improve their abilities through RL.

Methodology

Problem Formulation

Symbolic regression aims to find a symbolic expression that describes the underlying relationship in a dataset. 

given a dataset  

input vevtor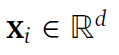 

scalar output 

an SR method seeks to find a concise symbolic function 𝑓 such that 

The goal of SR

1) discover a function that minimizes the error between the predicted values and the true values

2) generalizes well to unseen inputs while maintaining interpretability.

总之就是拟合一个表达

Inference Framework

Algorithm 1.，the overall inference framework.

创建一个“堆”结构（heap），用于按照误差或得分排序保存方程候选结果。

执行 N 轮迭代，每一轮都让 LLM 尝试改进当前方程。

• 第一轮：LLM 根据目标 G1​ 随机生成方程；

• 后续轮次：LLM 参考前一轮表现最好的 K 个方程（即 H.topk(K)），在此基础上改进生成（类似“进化”：用上轮好方程继续变异优化。）

把这轮得到的所有候选方程加入堆中，继续排序保存。

判断是否达到停止条件，如 1）当前最优 MAPE < 目标阈值；2）或者迭代次数太多、改进不明显。未满足则更新目标（例如收紧精度要求、调整搜索方向等）

循环结束后取堆中得分最高（误差最低）的方程作为最终结果

总之就是Goal → LLM Generate → Evaluate → Heap → UpdateGoal → Loop / Stop

At each iteration,  goal 𝐺𝑖 for a desired optimization precision and the agent is instructed to find an equation that satisfies the precision.

We choose the mean absolute percentage error (MAPE) as the goal: 

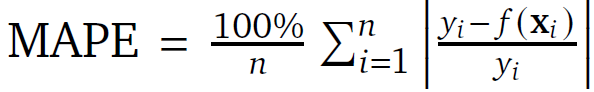
总之就是一种误差的计算方式了

Then, the LLM agent solves the problem by interleaving internal reasoning with external environment feedback. Formally, the agent’s trajectory is structured as follows, typically within a ReAct (Yao et al., 2023) framework:

𝑟𝑖 (推理）denotes the model’s natural language reasoning at step 𝑖,

T𝑖 ⊆ T  (工具）is the set of tools invoked at step 𝑖,

𝑜𝑖  (观察得到的结果）is the observation received after executing the tools in T𝑖
（maximum interaction turns 𝑀）（这个是防止一直不停下来的

Tool Design

code interpreter,  enabling the agent to write code for data analysis and performance evaluation, including data analyzer and equation evaluator: 

data analyzer T1:

input:  observed data, =a code example in the prompt demonstrating how to access the data

2) write code to analyze the data, including print-ing the data, conducting statistical analysis, or analyzing the residuals between the predicted value and the true value. 

equation evaluator T2 : 

input： equation skeleton with placeholders for constants in code format/equations with constants decided through other methods like data analysis (See Figure 1 or 5 for the equation example).

During the execution phase, the BFGS algorithm is implemented to optimize these constants and then report the performance of the equation. 

prevents the agent from writing repetitive code for equation evaluation during the long-horizon
exploration process.

Experience Buffer 

为了解决上下文长度提出的，同时在长时间解决之后还可能效果不好

we maintain an experience buffer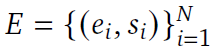 to record the equations the agent has explored, where 𝑒𝑖 denotes the equation and 𝑠𝑖 is its corresponding MAPE.

for each iteration, we fetch the best 𝐾 equations from the buffer and provide them to the agent as in-context examples (这个其实就是找之前几个比较好的例子，然后再在上面优化）The optimization goal is also updated if it was reached in the previous iteration. This mechanism effectively bypasses the context length limitation.

GP algorithms has no significant improvement for experience management. 所以还是基于大模型本身的对于先前例子的上下文积累得出新结论的

Stopping Condition and Submission

1. maximum number of iterations is reached

2. the equation’s error is sufficiently small.

Then, we select the equation with the best performance on the observed data and submit it for final evaluation.

Training Framework

Training Data Construction

we employ a mixed strategy of rule-based and model-based data synthesis. 

For each scientific scenario covering multiple variables, we

1）LLM 画“方程骨架”  instruct an LLM to synthesize potential relationships between variables in the form of an equation skeleton.

2）确定常数的物理含义和数值  For each skeleton, we use the model to determine the values for the constants based on their physical significance and thereby construct the full equation.

3）定义变量范围并合成观测数据  we define an appropriate range of values for its variables and synthesize the observed data accordingly.

4）划分训练集与评估集 split into training and evaluation sets

Reward Design

① 设定目标精度 𝑠goal 

也就是说，在每个 rollout（实验回合）开始前，给模型一个目标，比如

希望生成的方程误差 MAPE ≤ 0.05。

② 智能体生成多个方程并与环境交互

这一步中，模型会生成不同候选方程；每个方程会被执行、评估；得到其误差（MAPE 值）。

③ RL 环境中简化优化为单次迭代

为了降低计算复杂度，他们让每次 rollout 只包含一轮优化（不反复更新策略），
相当于一次性试完 → 计算奖励 → 再进入下一轮。

④ 使用连续奖励而非二元奖励

在很多 RL 任务（例如代码执行正确/错误）里，奖励是二元的（0 或 1）；但这里，方程好坏可以用 MAPE 的连续数值衡量，所以可以给出连续奖励，例如 0.3、0.7、0.95 等。这让模型能更细腻地感知“改进方向”，避免奖励稀疏（reward sparsity）

⑤ 从多次实验中选出最优方程用于计算奖励

他们不会给所有方程都奖励，而是只取当前轮中最好的方程；它的 MAPE 记为 s，用这个 s 来计算奖励值。

⑥ 使用一个**对数线性函数（log-linear reward function）**来将误差 s 转换成奖励值 R：

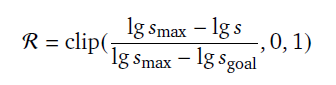
符号	含义
( s )	当前方程的 MAPE（越小越好）
( s_goal )	希望达到的目标误差（比如 0.05）
( s_max )	最差情况下仍能得到非零奖励的最大误差阈值
( clip(x,0,1) )	保证结果在 [0,1] 之间

Training Algorithm

核心是 Group Relative Policy Optimization (GRPO)，只是改成了组内比较的形式

1）用旧的策略采样一组输出 for each question 𝑞, we sample a group of outputs {𝑜1, 𝑜2, · · · , 𝑜𝐺} from the old policy 𝜋𝜃old 

2) 计算每个输出的奖励

每个输出 oi 会经过执行和评估，比如计算 MAPE（平均绝对百分比误差），再通过 reward function（上图那个 log-linear 奖励公式）得到奖励值。

这些奖励就用于计算每个输出的“相对优势”（advantage）：

也就是说：

• 如果 oi 在这一组里比平均好，Ai>0，模型应该更倾向生成它；

• 如果比平均差，Ai<0，模型应该减少生成它的概率。

3) 定义优化目标函数

（reward）optimize the policy 𝜋𝜃 by maximizing the following objective:

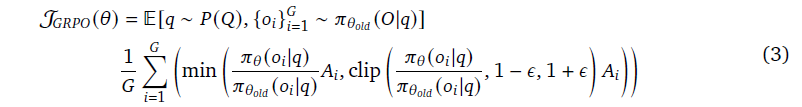
𝜀 is the hyper-parameter, and 𝐴𝑖 is the advantage computed using a group of rewards corresponding to the outputs within each group.

符号	含义
( \pi_\theta(o_i	q) )
( \pi_{\theta_{old}}(o_i	q) )
( \frac{\pi_\theta}{\pi_{\theta_{old}}} )	概率比，用于衡量“新策略偏离旧策略多少”
( A_i )	该输出的优势（相对好坏）
(𝜖 )	超参数，控制更新范围（防止训练崩溃）
clip(...)	限制概率比不超过 [1−ε, 1+ε]，保证训练稳定

注意，这里去掉了kl 惩罚项：We omit the KL penalty term against a reference model and observe that this leads to faster convergence and comparable performance.

总的来说就是： 每个任务让模型生成多个结果；模型自己比较这些结果哪一个好（根据 MAPE 奖励）；如果某个结果更好，就让模型在未来更倾向于生成类似的输出；同时控制更新步幅，防止一次改太多。

Experiment 

这里我也就是看个思路，要细节自己去搜论文看

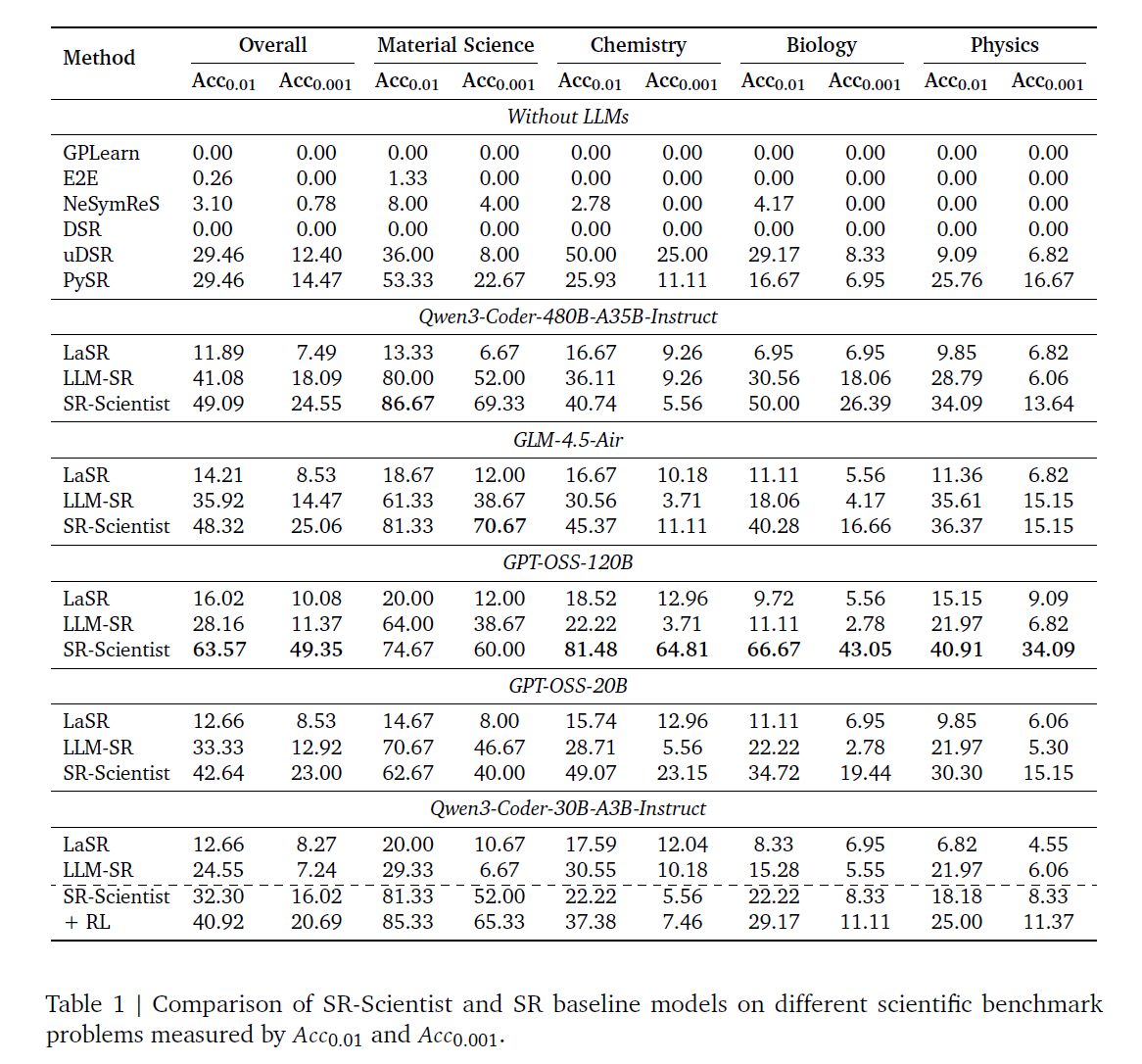
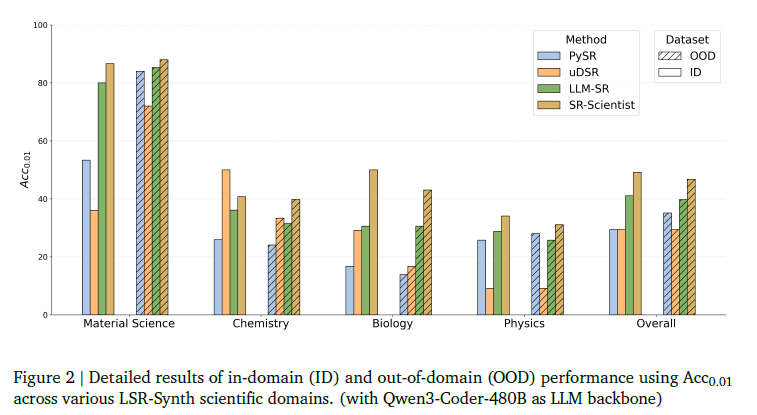
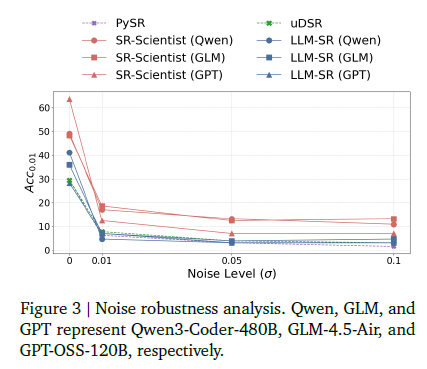
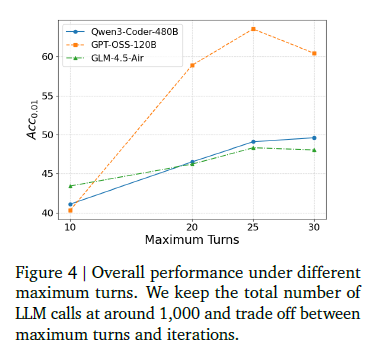
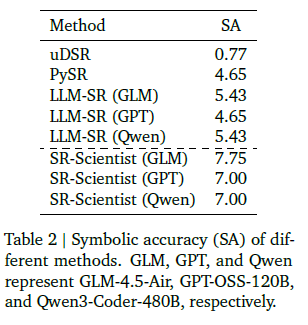
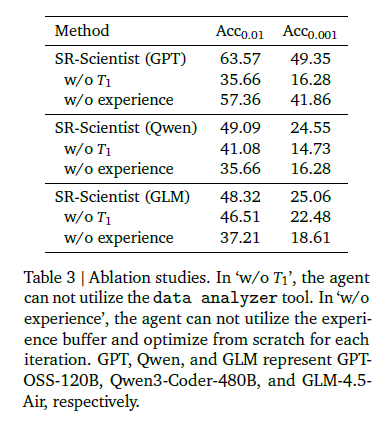
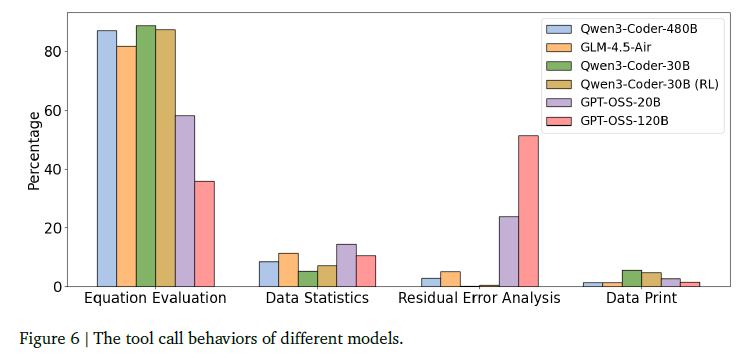
Conclusion

在本文中，我们介绍了 SR-Scientist 框架，该框架将大型语言模型从被动的方程提出者转变为用于符号回归的自主科学家。通过分析数据、评估和优化方程，该智能体通过主动与环境交互生成并优化假设。我们的实验表明，SR-Scientist 在精度、泛化能力、对噪声的鲁棒性以及符号准确性方面显著优于现有方法。此外，我们开发了一个完整的强化学习管道，使智能体能够自我进化并增强其发现能力。