最小 k 个数

目录

一：题目链接

二：题目思路

三：代码实现

---

一：题目链接

二：题目思路

这道题，是在 快速排序 的基础上解决的，在此之前，请务必了解快排的实现逻辑。

        我们完成一次 数组分三块 的操作后，对这三块数组进行分析：

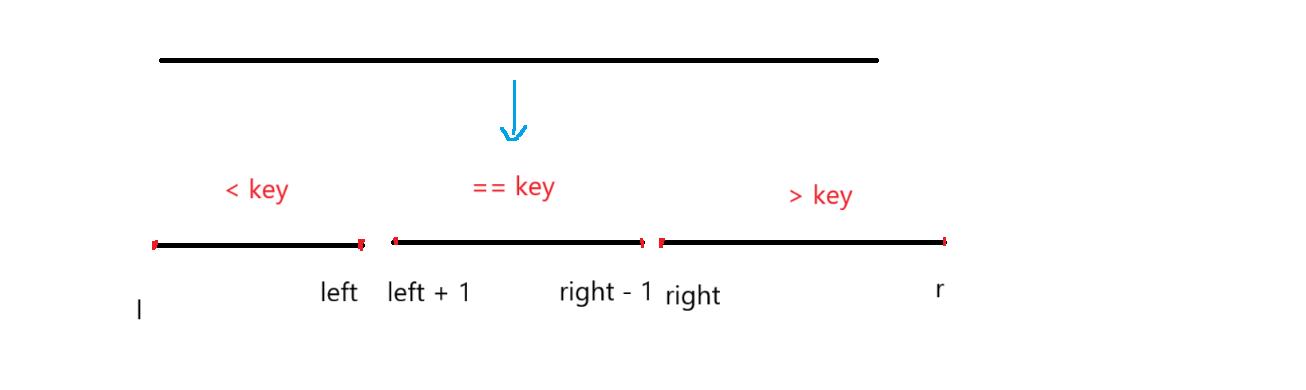
        三个区间的元素个数分别为 a = left - l + 1 ，b = (right - 1) - (left + 1) + 1 ， c = r - right + 1。

        当 a > k 时，说明这 k 个最小的元素在 a 这个区间里，所以后面的两个区间不用管了，直接对 a 区间继续进行快速排序。

        当 a + b >= k 时，说明这 k 个最小的元素一部分在 a 区间，一部分在 b 区间，又因为 b 区间元素都是相等的，所以可以直接返回。

        剩余的情况，说明这 k 个最小的元素 包含 a区间 和 b 区间，一部分在 c 区间，再去 c 区间寻找前 k - a - b 个最小的元素。 

        完成上述过程后，数组可能不一定会全部排序成升序，但排序的区域足以返回结果了。

三：代码实现

    public int[] smallestK(int[] nums, int k) {qsort(nums,0,nums.length - 1,k);int[] ret = new int[k];for(int i = 0;i < k;i++) {ret[i] = nums[i];}   return ret;}public void qsort(int[] nums,int l,int r,int k) {//判断if(l >= r) {return;}//取基准数int key = nums[new Random().nextInt(r - l + 1) + l];//主逻辑int left = l - 1;int right = r + 1;int i = l;while(i < right) {if(nums[i] < key) {swap(nums,++left,i++);}else if(nums[i] == key) {i++;}else {swap(nums,--right,i);}}//寻找最小的 k 个数int a = left - l + 1;int b = (right - 1) - (left + 1) + 1;if(a > k) {qsort(nums,l,left,k);}else if(a == k || a + b >= k) {return;}else {qsort(nums,right,r,k - a - b);}}public void swap(int[] nums,int a,int b) {int c = nums[a];nums[a] = nums[b];nums[b] = c;}