当前位置：首页 > news >正文

算法题逆波兰表达式/计算器

news 2025/10/29 11:19:05

题一:逆波兰表达式(后缀表达式)

什么是逆波兰表达式?

逆波兰表达式（也称为后缀表达式）的核心逻辑是将运算符放在其对应的所有操作数之后，从而消除表达式中的括号和运算符优先级歧义，让计算机能通过栈结构高效计算。

逆波兰表达式必须严格遵循“操作数在前、运算符紧跟对应操作数”的顺序，否则会导致计算逻辑混乱。数字的顺序与原始中缀表达式中操作数的自然出现顺序保持一致，无需调整数字的先后顺序，只需将运算符按“作用于对应操作数之后”的规则后置即可。

代码实现:

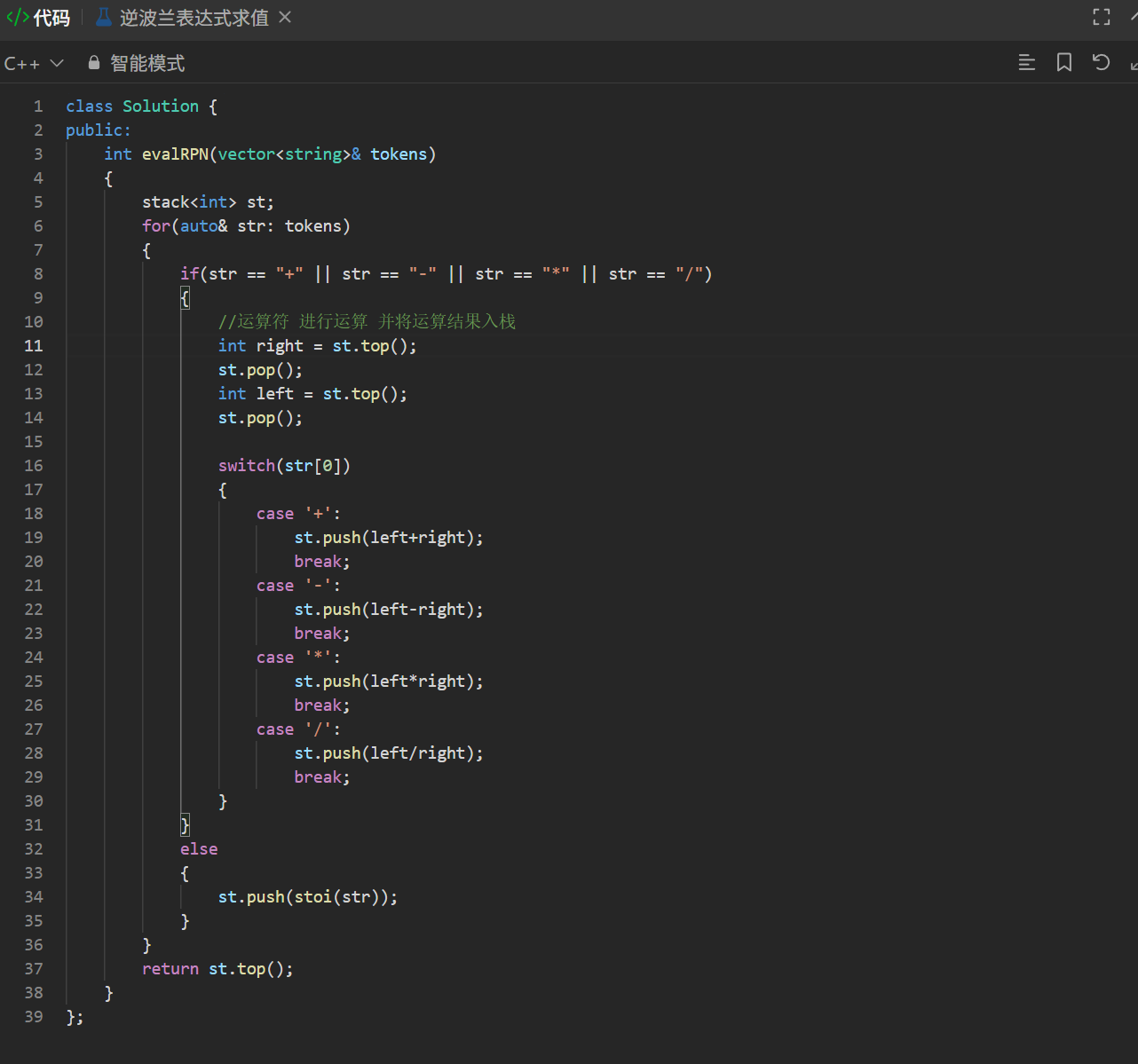
思路:

逆波兰表达式的特点是“运算符位于其对应操作数之后”，例如表达式 ["3","4","+"] 对应中缀式 3+4 。代码的核心是：

1. 遍历表达式的每个元素（ tokens 中的字符串）；
2. 遇到数字时，将其转换为整数并压入栈中；
3. 遇到运算符时，从栈中弹出两个操作数（先弹出的是“右操作数”，后弹出的是“左操作数”），用运算符计算两者的结果，再将结果压回栈中；
4. 遍历结束后，栈中仅剩的一个元素就是表达式的最终结果。

举个例子（以表达式 ["2","1","+","3","*"] 为例，对应中缀式 (2+1)*3 ）：

1. 遍历到 "2" ：压栈 → 栈： [2] ；
2. 遍历到 "1" ：压栈 → 栈： [2,1] ；
3. 遍历到 "+" ：弹出 1 （ right ）和 2 （ left ），计算 2+1=3 ，压栈 → 栈： [3] ；
4. 遍历到 "3" ：压栈 → 栈： [3,3] ；
5. 遍历到 "*" ：弹出 3 （ right ）和 3 （ left ），计算 3*3=9 ，压栈 → 栈： [9] ；
6. 返回 st.top() → 结果为 9 。

借助栈的方式，完美契合了逆波兰表达式“先存操作数、后算运算符”的特性

注意点:

1. 函数形参用 vector<string> 而非 string 的简化道理
逆波兰表达式的输入是由多个“原子单元”组成的（每个单元是数字或运算符，如 ["3","+","4"] ）。若直接用 string  作为形参，需要手动分割字符串（比如按空格或字符边界拆分出每个单元），这会增加代码复杂度。而 vector<string>  已经将表达式预拆分为一个个独立的“token”（标记），直接遍历每个 string  即可，省去了手动分割字符串的步骤，让核心的“栈计算逻辑”更简洁。

2. if  语句中 ==  用 "" （双引号）的原因
本题中 str 被定义为 string  类型（从代码里的判断逻辑 str == "+"  等能看出是字符串比较），而单引号 '+'  表示的是字符（ char  类型），字符串（ string ）和字符（ char ）是不同的类型，无法直接用 ==  进行比较。

字符串（ string ）：用双引号包裹，string本质是字符数组（ char[] ），存储时包含字符和结束符 \0 ，例如 "+" 实际存储的是 '+' 和 \0 。
字符（ char ）：用单引号包裹，是单个字符，例如 '+' 就是一个字符常量。

如果强行用单引号（比如写成 str == '+' ），会因为类型不匹配导致编译错误（编译器会认为你在拿 string  和 char  做比较，这两种类型没有默认的 ==  重载）。

3. switch  语句用 str[0]  的原因
str  是表示运算符的 string （如 "+" 、 "-" ），而 switch  语句的条件要求是整型或字符型（C++ 中 switch  不支持 string  类型）。 str[0]  可以获取字符串的第一个字符（如 "+"  的 str[0]  是 '+' ， "-"  的 str[0]  是 '-' ），这是一个 char  类型，符合 switch  的语法要求，因此用 str[0]  作为分支判断的条件。

4. 最后用 stoi  的原因
tokens  中的元素是 string  类型（如 "5" 、 "12" ），而栈 st  存储的是 int  类型的操作数。 stoi （string to integer）函数的作用是将字符串形式的数字转换为整数（比如把 "5"  转成 5 ，把 "12"  转成 12 ），这样才能将字符串类型的数字存入整数栈中，供后续的运算使用。

中缀转后缀

为什么要实现中缀转后缀呢?

中缀表达式（如 a+b*c ）的运算符位于操作数之间，人类容易理解，但计算机直接解析时，需处理复杂的优先级（如 * 优先于 + ）和括号嵌套，极易出错。而逆波兰表达式（如 a b c * + ）将运算符放在操作数之后，结构天然适合“遇数入栈、遇运算符出栈计算”的逻辑，因此需要先完成这种转换。

那么中缀表达式怎么转为后缀表达式呢?

#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<assert.h>
using namespace std;class Solution
{
public://map<char,int> _operatorPrecedence{{'+' , 1} ,{ '-' , 1 } ,{ '*' , 2 }, { '/' , 2 }};int operatorPrecedence(char ch){struct opPD{char _op;int _pd;};static opPD arr[] = { {'+' , 1} ,{ '-' , 1 } ,{ '*' , 2 }, { '/' , 2 } };for (auto& e : arr){if (e._op == ch){return e._pd;}}assert(false);return -1;}//中缀转后缀void toRPN(const string& s, size_t& i, vector<string>& v){stack<int> st;while (i < s.size()){//操作数直接输出if (isdigit(s[i])){string num;while(i<s.size() && isdigit(s[i])){num += s[i];++i;}v.push_back(num);}else if (s[i] == '('){//子表达式 , 递归处理++i;toRPN(s, i, v);}else if (s[i] == ')'){//子表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}++i;return;}else{//运算符if (st.empty() || operatorPrecedence(s[i]) > operatorPrecedence(st.top())){st.push(s[i]);++i;}else{char op = st.top();st.pop();v.push_back(string(1,op));}}}//表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}}
};int main()
{size_t i = 0;vector<string> v;string str1 = "1+2-3";Solution().toRPN(str1, i, v);for (auto& e : v){cout << e << " ";}cout << endl;string str2 = "1+2-(3*4+5)-7";i = 0;      //重置v.clear();   //清空Solution().toRPN(str2, i, v);for (auto& e : v){cout << e << " ";}cout << endl;return 0;
}

思路:

代码通过 toRPN 函数实现转换，接收中缀表达式字符串 s 、当前遍历位置 i （引用传递，确保递归和连续遍历）、结果容器 v （存储后缀表达式的“token”，即数字或运算符字符串）。整个转换过程可分为以下关键步骤：

（1）处理数字操作数
当遍历到数字字符时，会连续拼接所有连续的数字字符，形成完整的数字字符串（例如将 '1' 、 '2' 拼接成 "12" ），然后将这个数字字符串直接加入结果容器 v 。这一步确保每个数字作为独立的“token”被正确识别。

（2）处理左括号 ' ( ' ：递归深入子表达式
遇到左括号时，说明进入了一个子表达式（如 (3*4+5) ）。此时：

- 先将遍历索引 i  后移（跳过左括号）；
- 递归调用 toRPN  函数，处理子表达式内部的内容；
- 子表达式处理完成后，右括号会触发递归返回，继续处理外层表达式。

（3）处理右括号 ' ) ' ：弹出栈中所有运算符
遇到右括号时，说明子表达式结束，需要将栈中所有未弹出的运算符输出到结果 v  中（这些运算符属于子表达式内部的优先级处理）。例如，子表达式 3*4+5  转换后，栈中可能残留 + ，右括号会触发这些运算符的弹出，然后后移索引 i  并结束当前子表达式的递归处理。

（4）处理运算符（+、-、*、/）：基于优先级的栈操作
遇到运算符时，需根据运算符优先级决定是否将栈中已有运算符弹出到结果中：

- 若栈为空，或当前运算符优先级高于栈顶运算符的优先级（例如 *  优先级高于 + ）：将当前运算符压入栈，等待后续处理；
- 若当前运算符优先级不高于栈顶运算符的优先级（例如 +  优先级不高于 * ）：弹出栈顶运算符，加入结果 v ，重复此判断直到满足压栈条件，再将当前运算符压入栈。
这样可以保证运算符按正确的优先级顺序输出到结果中（如 a+b*c  转换为 a b c * + ）。

（5）表达式遍历结束：清理栈中剩余运算符
当遍历完整个中缀表达式字符串 s  后，栈中可能仍有未弹出的运算符（如表达式末尾的运算符），需要将它们全部弹出并加入结果 v ，确保所有运算符都被正确转换到后缀表达式中。

（6）运算符优先级的辅助判断
operatorPrecedence  函数用于返回运算符的优先级（乘除 * 、 /  优先级为2，加减 + 、 -  优先级为1），是判断“何时压栈、何时弹栈”的核心依据。通过自定义结构体数组存储“运算符-优先级”的映射关系，实现高效的优先级查找。

最终效果:

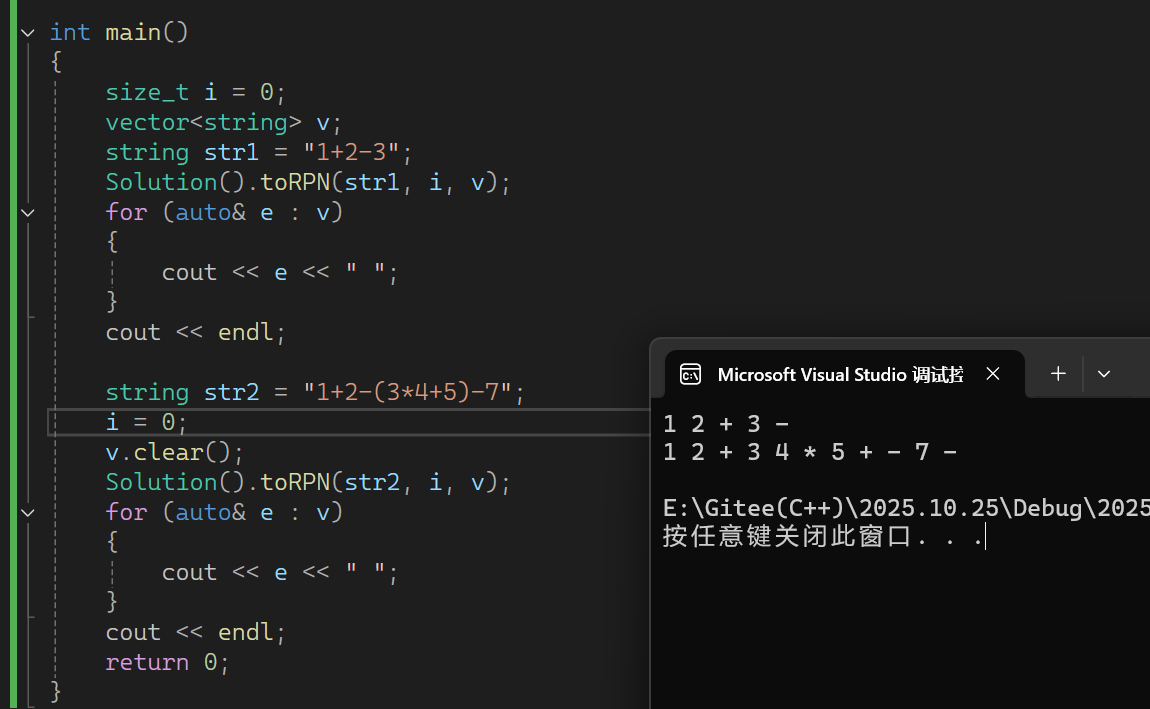
在 main 函数中，定义中缀表达式（如 1+2-(3*4+5)-7 ），调用 toRPN 完成转换后，结果容器 v 中会存储对应的后缀表达式token（如 1 2 + 3 4 * 5 + - 7 - ），后续可通过栈结构（如 evalRPN 函数）快速计算出表达式的值。

题二: 基本计算器

下面再来看一道更有难度的OJ题:

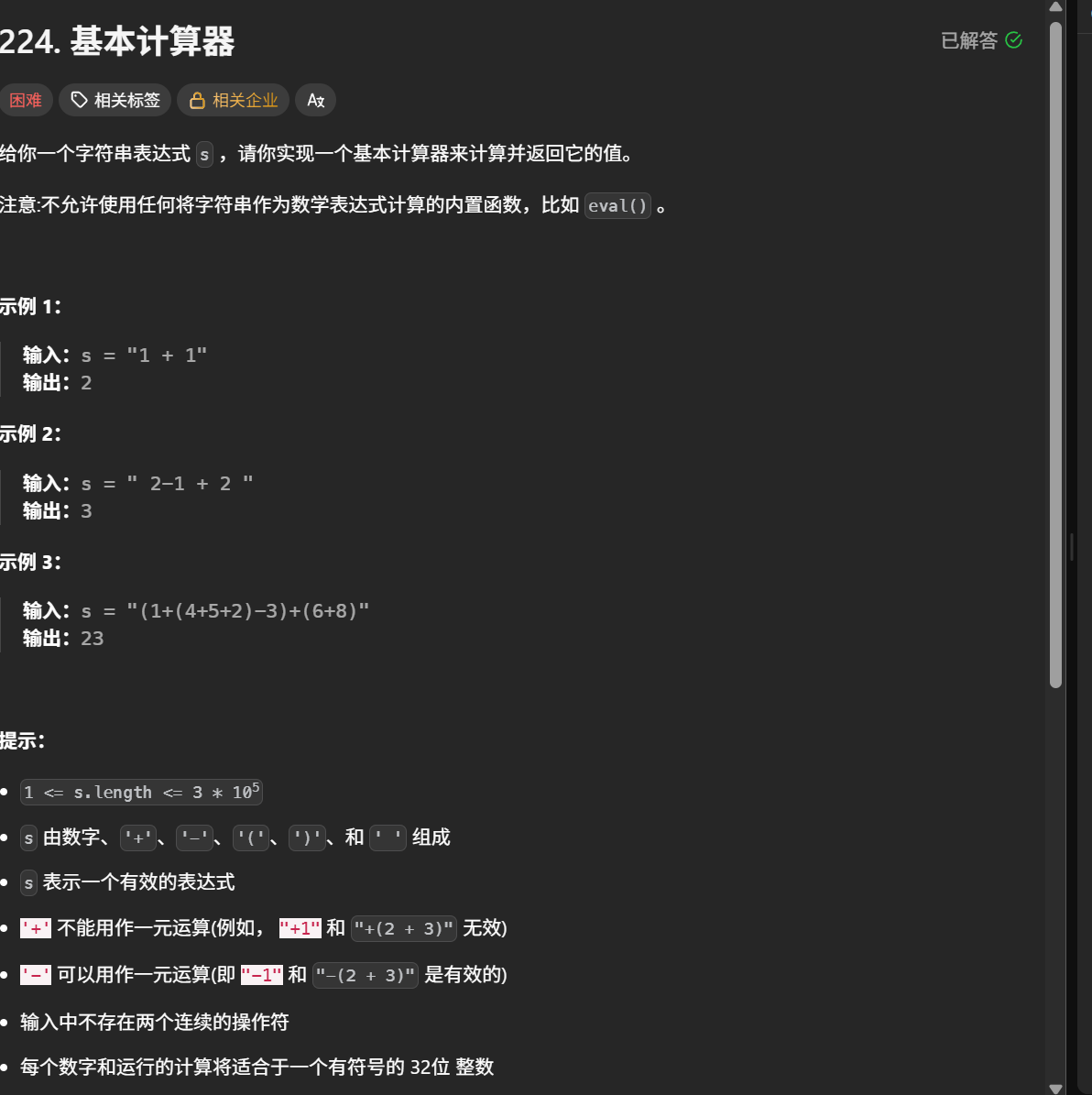
从题目要求来看，输入的表达式 s 确实只包含加减、括号和空格，没有乘除运算。但是小编在代码中对乘除（ * 、 / ）的逻辑进行了额外实现，但这并不影响代码的正确性 , 属于对计算器功能的扩展

代码实现:

class Solution {
public:int evalRPN(vector<string>& tokens){stack<int> st;for (auto& str : tokens){if (str == "+" || str == "-" || str == "*" || str == "/"){//运算符 进行运算 并将运算结果入栈int right = st.top();st.pop();int left = st.top();st.pop();switch (str[0]){case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;}}else{st.push(stoi(str));}}return st.top();}
int operatorPrecedence(char ch)
{struct opPD{char _op;int _pd;};static opPD arr[] = { {'+' , 1} ,{ '-' , 1 } ,{ '*' , 2 }, { '/' , 2 } };for (auto& e : arr){if (e._op == ch){return e._pd;}}assert(false);return -1;
}
//中缀转后缀
void toRPN(const string& s, size_t& i, vector<string>& v)
{stack<int> st;while (i < s.size()){//操作数直接输出if (isdigit(s[i])){string num;while(i<s.size() && isdigit(s[i])){num += s[i];++i;}v.push_back(num);}else if (s[i] == '('){//子表达式 , 递归处理++i;toRPN(s, i, v);}else if (s[i] == ')'){//子表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}++i;return;}else{//运算符if (st.empty() || operatorPrecedence(s[i]) > operatorPrecedence(st.top())){st.push(s[i]);++i;}else{char op = st.top();st.pop();v.push_back(string(1,op));}}}//表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}
}int calculate(string s) {string news;for (auto& ch : s){if (ch != ' '){news += ch;}}news.swap(s);news.clear();for (size_t i = 0;i < s.size();++i){if (s[i] == '-' && (i == 0 || (!isdigit(s[i - 1]) && s[i - 1] != ')'))){news += "0-";}else{news += s[i];}}cout << news << endl;size_t i = 0;vector<string> v;toRPN(news, i, v);return evalRPN(v);}
};

思路:

解答这道题就要结合上面的题一和中缀转后缀的代码:

步骤1：输入预处理：过滤空格，并处理负号（如 -1 补全为 0-1 ，避免作为一元运算符的歧义）。
步骤2：中缀转后缀（ toRPN 函数）：利用栈管理运算符优先级（本题中加减优先级相同），处理括号嵌套，将中缀表达式转换为后缀表达式的 vector<string> 。
步骤3：后缀表达式求值（ evalRPN 函数）：用栈存储操作数，遇到运算符时弹出栈顶两个数计算，结果再入栈，最终栈顶即为表达式结果。

evalRPN函数：后缀表达式求值
- 遍历后缀表达式的每个 token ：
- 若为数字，转整数并入栈；
- 若为运算符（ + 、 - ），弹出栈顶两个数，按运算符计算后将结果入栈。
operatorPrecedence函数：运算符优先级（本题简化为加减优先级相同）
由于题目仅涉及 + 、 - ，返回固定优先级（如都为 1 ），确保运算符处理逻辑统一。
toRPN函数：中缀转后缀
- 数字处理：连续拼接数字字符，形成完整数字字符串并入结果。
- 括号处理：遇到 ( 则递归处理子表达式；遇到 ) 则弹出栈中所有运算符直到遇到 ( ，并丢弃 ( 。
- 运算符处理：由于加减优先级相同，遇到运算符时弹出栈中所有已有运算符，再将当前运算符入栈；遍历结束后弹出栈中剩余运算符。
calculate函数：总入口
- 预处理输入字符串（过滤空格、补全负号），调用 toRPN 转后缀，再调用 evalRPN 计算结果并返回。

注意点:

过滤空格

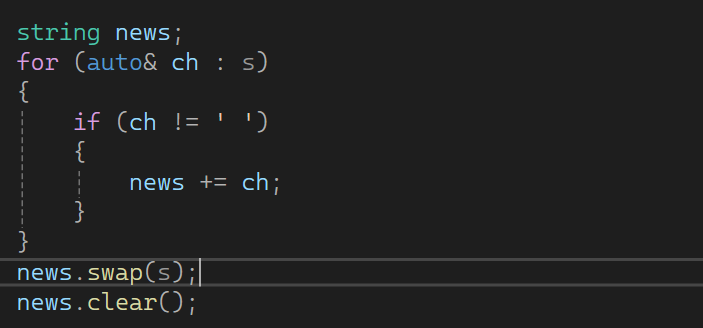
作用：遍历原始字符串 s ，将所有非空格字符拼接至 news ，实现过滤空格的效果（比如输入 "1 + 1" 会被处理为 "1+1" ）。
news.swap(s) ：交换 news 和 s 的内容，此时 s 变为过滤空格后的字符串， news 变为空（为后续补全负号腾出空间）。

补全负号

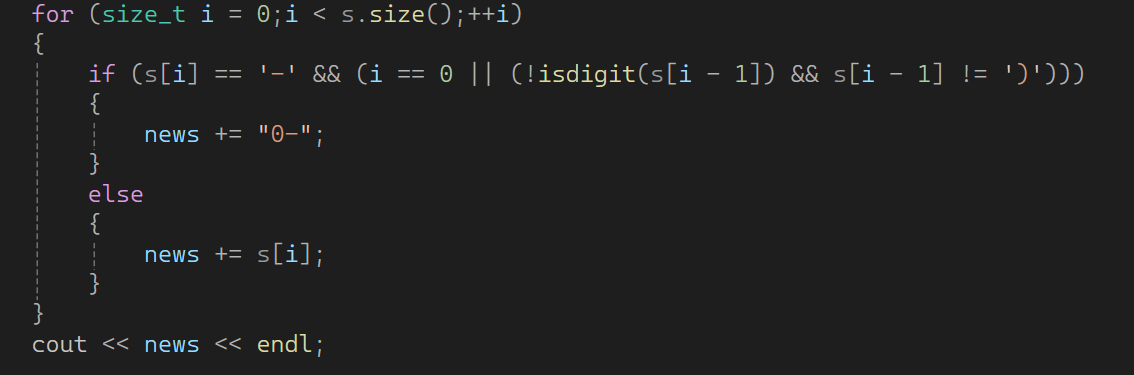
作用：处理“一元负号”（如 -1 、 -(2+3) ），将其补全为“二元减法形式”（如 0-1 、 0-(2+3) ），避免表达式解析时的歧义。
条件判断 s[i] == '-' && (i == 0 || (!isdigit(s[i - 1]) && s[i - 1] != ')')) ：
s[i] == '-' ：当前字符是负号；
i == 0 ：负号在字符串开头（如 -123 ）；
!isdigit(s[i - 1]) && s[i - 1] != ')' ：负号前不是数字且不是右括号（如 +( -2) 中的负号）。
满足以上条件时，说明是一元负号，需要补全为 0- （将一元运算转为二元减法）。

经过这段预处理后，字符串会被转换为“无空格 + 负号补全”的规范形式，例如：

输入： " -1 + (2-3) "
处理后： "0-1+(2-3)" （过滤空格 + 开头负号补全为 0- ）。

为何需要这步处理？在计算器表达式解析中：

空格会干扰字符遍历，必须过滤；
负号既可以是“二元运算符”（如 1-2 ），也可以是“一元运算符”（如 -3 ），补全为 0- 后，能统一按“二元减法”逻辑解析，简化后续中缀转后缀的复杂度。

基本计算器的完整实现

完整实现:

#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<assert.h>
using namespace std;class Solution
{
public://用后缀计算答案int evalRPN(vector<string>& tokens){stack<int> st;for (auto& str : tokens){if (str == "+" || str == "-" || str == "*" || str == "/"){//运算符 进行运算 并将运算结果入栈int right = st.top();st.pop();int left = st.top();st.pop();switch (str[0]){case '+':st.push(left + right);break;case '-':st.push(left - right);break;case '*':st.push(left * right);break;case '/':st.push(left / right);break;}}else{st.push(stoi(str));}}return st.top();}//map<char,int> _operatorPrecedence{{'+' , 1} ,{ '-' , 1 } ,{ '*' , 2 }, { '/' , 2 }};int operatorPrecedence(char ch){struct opPD{char _op;int _pd;};static opPD arr[] = { {'+' , 1} ,{ '-' , 1 } ,{ '*' , 2 }, { '/' , 2 } };for (auto& e : arr){if (e._op == ch){return e._pd;}}assert(false);return -1;}//中缀转后缀void toRPN(const string& s, size_t& i, vector<string>& v){stack<int> st;while (i < s.size()){//操作数直接输出if (isdigit(s[i])){string num;while (i < s.size() && isdigit(s[i])){num += s[i];++i;}v.push_back(num);}else if (s[i] == '('){//子表达式 , 递归处理++i;toRPN(s, i, v);}else if (s[i] == ')'){//子表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}++i;return;}else{//运算符if (st.empty() || operatorPrecedence(s[i]) > operatorPrecedence(st.top())){st.push(s[i]);++i;}else{char op = st.top();st.pop();v.push_back(string(1, op));}}}//表达式结束//输出栈里面剩余的运算符while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}}
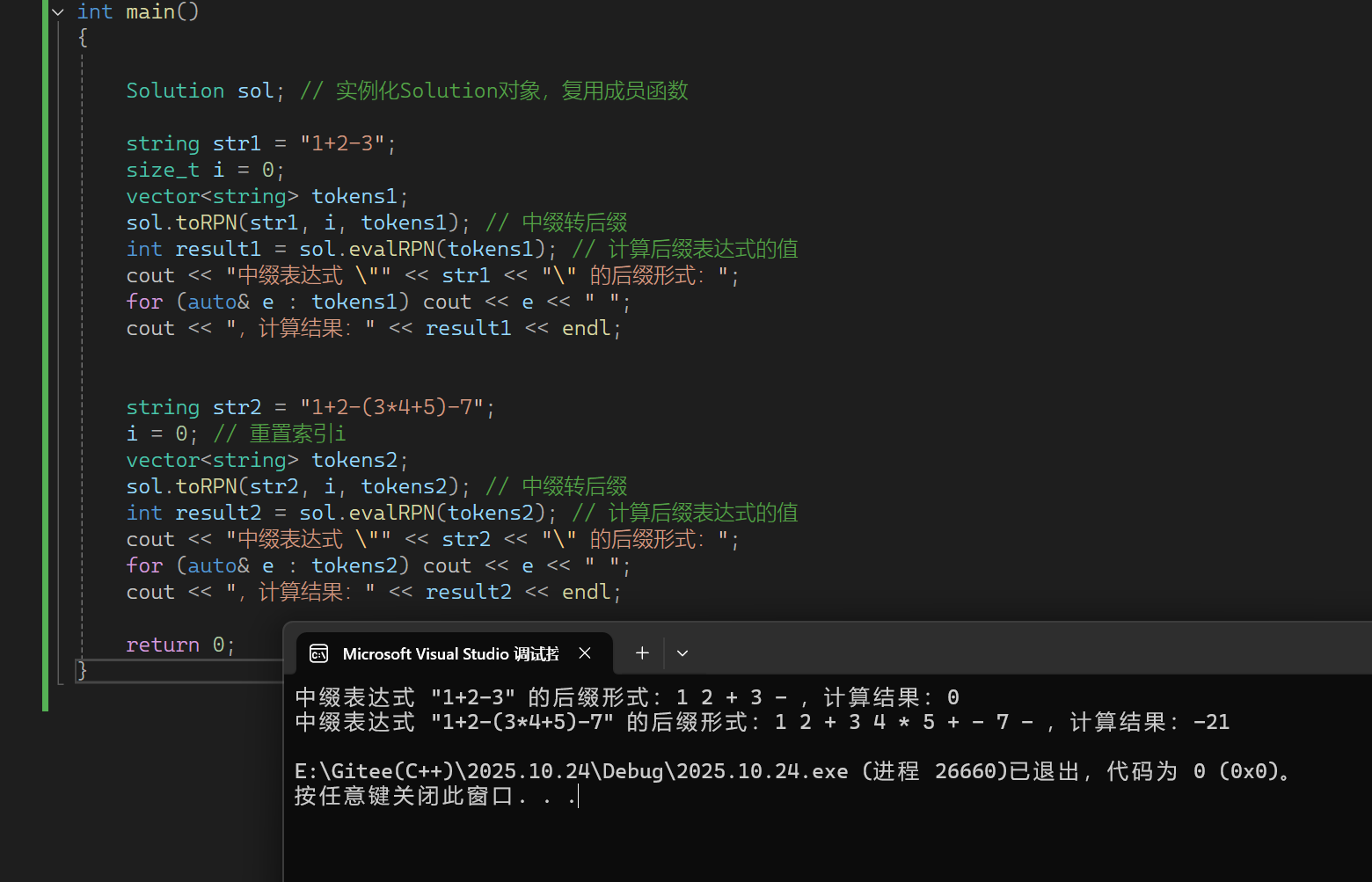
};int main()
{Solution sol; // 实例化Solution对象，复用成员函数string str1 = "1+2-3";size_t i = 0;vector<string> tokens1;sol.toRPN(str1, i, tokens1); // 中缀转后缀int result1 = sol.evalRPN(tokens1); // 计算后缀表达式的值cout << "中缀表达式 \"" << str1 << "\" 的后缀形式：";for (auto& e : tokens1) cout << e << " ";cout << "，计算结果：" << result1 << endl;string str2 = "1+2-(3*4+5)-7";i = 0; // 重置索引ivector<string> tokens2;sol.toRPN(str2, i, tokens2); // 中缀转后缀int result2 = sol.evalRPN(tokens2); // 计算后缀表达式的值cout << "中缀表达式 \"" << str2 << "\" 的后缀形式：";for (auto& e : tokens2) cout << e << " ";cout << "，计算结果：" << result2 << endl;return 0;
}

实现结果:

总结:

本文介绍了逆波兰表达式（后缀表达式）及其计算实现方法。逆波兰表达式将运算符置于操作数之后，通过栈结构实现高效计算。主要内容包括：1）逆波兰表达式概念及计算原理，通过栈结构处理数字和运算符；2）中缀表达式转后缀表达式的方法，使用栈管理运算符优先级和括号嵌套；3）计算器实现方案，结合预处理、中缀转后缀和后缀表达式求值三个步骤完成复杂表达式计算。文章通过具体代码示例展示了从表达式转换到最终计算的完整流程，并详细解释了各步骤的实现逻辑和注意事项。

查看全文

http://www.dtcms.com/a/541561.html