数据结构——三十二、最短路径问题——BFS算法(王道408)

前言

本文介绍了求解无权图单源最短路径的BFS算法。首先对最短路径问题进行了分类，分为单源最短路径和每对顶点间最短路径，分别对应BFS/Dijkstra和Floyd算法。重点讲解了BFS算法的实现过程：通过队列逐层遍历，记录各顶点到源点的距离和路径前驱，最终得到最短路径。相比普通BFS，增加了距离数组d和前驱数组path的记录。文章还指出广度优先生成树的层数反映了顶点到源点的最短距离。最后附上了代码实现和示例图解，帮助理解算法执行过程。

一.最短路径问题

1.单源最短路径问题

1.通俗理解

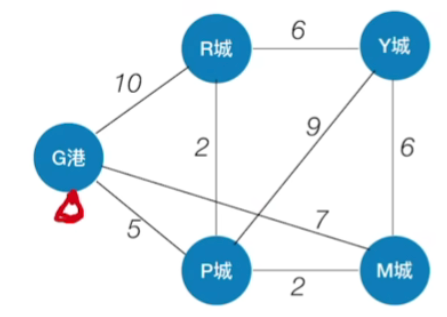
• 单源指的就是只有单独的一个源头,这个源头出发到达其他任意一个顶点,可以走的最短路径是什么

2.解决方法

1. BFS算法:用于解决无权图
2. Dijkstra算法:用于解决带权图或无权图

2.每对顶点间的最短路径

1.通俗理解

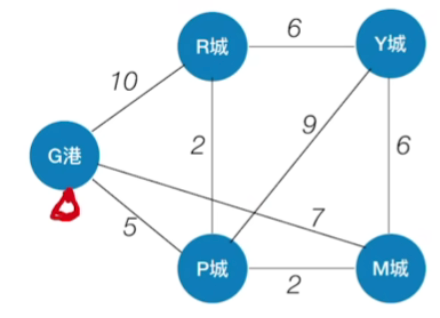
• 需要确定每一对顶点之间最短的路径

2.解决方法

• Floyd算法:用于解决带权图或无权图

二.BFS求无权图的单源最短路径

注：无权图可以视为一种特殊的带权图，只是每条边的权值都为1

1.方法例子

• 求出2这个顶点到达其他所有顶点的路径
  

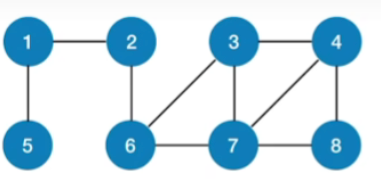
1. 从2这个顶点出发,那么可以找到和它相邻的顶点1和6,那和他直接相邻的两个顶点,显然距离就应该是1
   

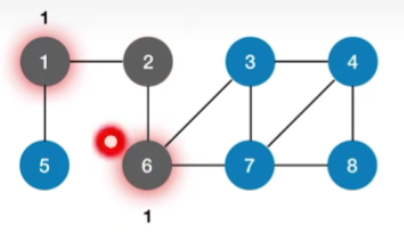
2. 接下来再通过1和6找到再下一层相邻的顶点也就是5,3,7,那么第二波找到的这些顶点,和原点2的距离就应该是2
   

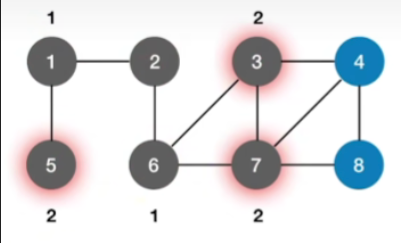
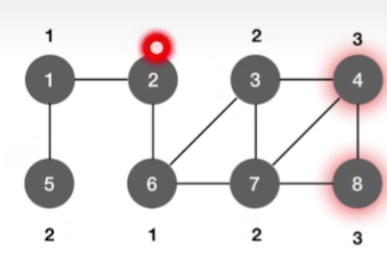
3. 重复上述操作,直到所有元素全部被遍历完,最终结果如下
   

2.代码实现

1.代码展示

//求顶点 u 到其他顶点的最短路径
void BFS_MIN_Distance(Graph G,int u){//d[i]表示从u到第i点的最短路径for(i=0;i<G.vexnum;++i){d[i]=∞;	//初始化路径长度path[i]=-1;	//最短路径从哪个顶点过来}d[u]=0;visited[u]=TRUE;EnQueue(Q,u);while(!isEmpty(Q)){	//BFS算法主过程DeQueue(Q,u);	//队头元素u出队for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))if(!visited[w]){	//w为u的尚未访问的邻接顶点d[w]=d[u]+1;	//路径长度加1path[w]=u;	//最短路径应从u到wvisited[w]=TRUE;	//设已访问标记EnQueue(Q,w);	//顶点w入队}//if}//while
}

2.代码过程

1. 要从2号顶点到达其他顶点的最短路径,也就是这个传入的u等于2

2. 那刚开始我们需要把d这个数组,所有的值都设为无穷,然后pass数组全部设为-1
   

3. 接下来d[u]=0会把2号顶点的d这个数组的值设为0,因为2号本来就是起始顶点,所以从起始顶点到达2号顶点的最短距离肯定是0,所以我们在这儿把它设为0
   

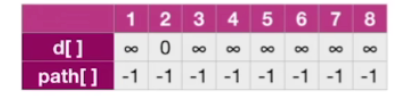
4. 那后面的visited[u]=TRUE;EnQueue(Q,u);和广度优先是一样的,我们需要标记2号顶点是已经被访问过的,然后把2号顶点放到一个队列当中
   

5. 接下来执行while循环,如果队列非空的话,那么就弹出队头元素也就是2号元素

6. 接下来从2号这个顶点开始出发,然后找到和它相邻的所有顶点,如果其中的某一些顶点没有被访问过,visit值等于false的话,那么我们就需要更改这些顶点的最短路径的长度

7. 那现在可以找到的是1号和6号这两个顶点,所以从2到1的最短路径就应该是2的d的值再加上1,因此我们需要把d[1]改成1,那同样的6这个顶点,我们也需要把它的地址改成1

8. 另外还有一个需要修改的地方,就是这个pass数组,我们需要在里边记录这条最短路径是从哪儿过来的,那1号顶点是从2号这直接过来的,所以它的上一个直接前驱应该是2号顶点,那同样的6号也是从2号过来的,所以它的上一个直接前驱应该是2号顶点,因此1号和6号的path值为2
   

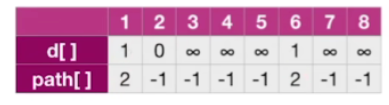
9. 接下来将已经访问的元素,即1和6的visited值设为true,同时将其放入队列
   

10. 后面的过程也是类似的,一直循环到队列为空为止,最终结果如下
    

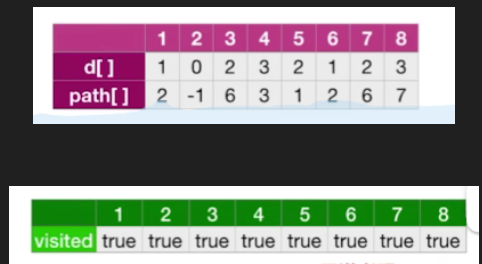
3.与之前小节中的BFS算法的不同之处

1. 增加了这样的两个数组
   1. 第一个数组d是用来记录各个顶点到原始顶点的最短路径的长度
   2. 第二个数组是用来记录每一个顶点在这个最短路径上的直接前驱
2. visted函数更改为了记录当前的路径长度与最短路径长度

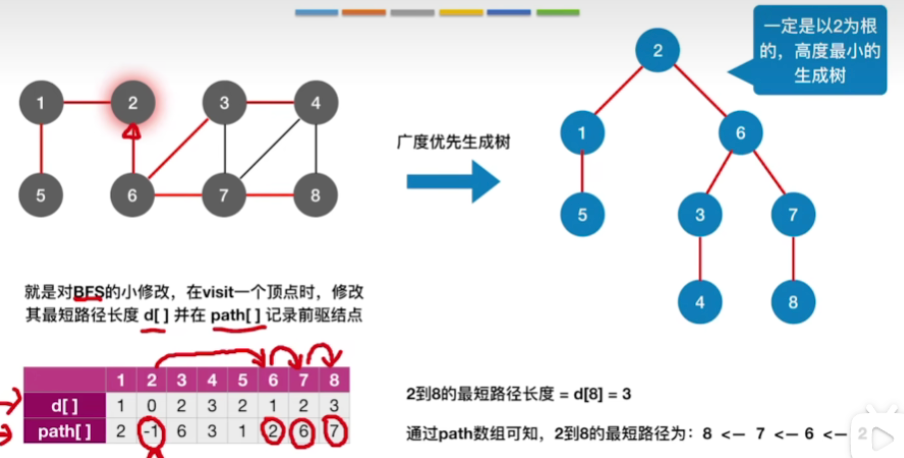
4.广度优先生成树求最短路径

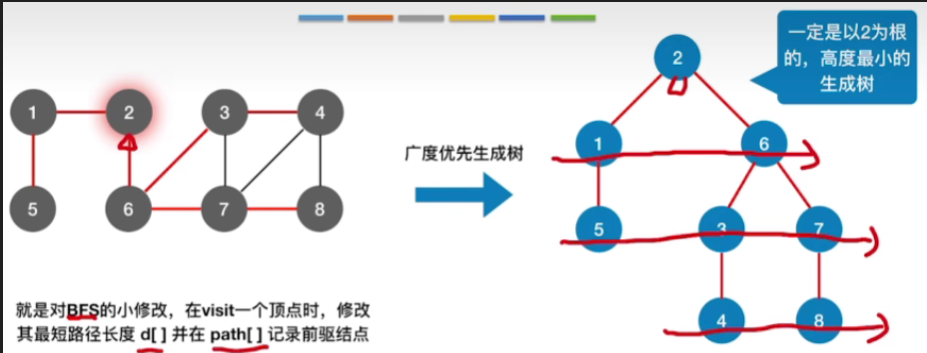
• 通过广度优先便利,可以得到一个广度优先生成树
• 其实这个生成树,每一个节点它到底在第几层,也直接地反映了从起点2到达这些节点的距离到底是多少
• 那既然是最短路径,其实就意味着说如果我们以2号顶点为根节点来构造一个生成树的话那么我们用广度优先构造出来的这个生成树它的深度或者说它的高度肯定是最小的

三.知识回顾与重要考点

结语

懈怠了,太懈怠了,拖更了四天,这四天和同学玩嗨了,以后绝对不会有这种事了

如果想查看更多章节,请点击:一、数据结构专栏导航页