当前位置：首页 > news >正文

数据结构（11）

news 2025/10/28 11:30:29

图的存储结构——图的遍历

一、深度优先搜索（DFS）—— 仿树的先序遍历过程

1、DFS 与树的先序遍历的相似性

2、DFS 的实现（突出与树先序的对比）

3、与树先序遍历的关键差异

4、示例对比：树的先序遍历 vs 图的 DFS

5、DFS算法效率分析

图的存储结构——图的遍历

实质：找每个顶点的邻接点的过程

设置一个辅助数组visited[n]，初始状态为0，被访问过改为1

一、深度优先搜索（DFS）—— 仿树的先序遍历过程

图的深度优先搜索（DFS）与树的先序遍历在逻辑上高度相似，均遵循 “先访问当前节点，再递归访问其分支” 的核心思路，因此常被称为 “仿树的先序遍历过程”。但由于图存在回路和多路径特性，DFS 需要额外的 “访问标记” 机制避免重复访问，而树的先序遍历因无环结构可直接递归。

核心思想：“一路走到底，碰壁再回头”

从起始顶点出发，优先沿着一条路径深入访问，直到无法继续（所有邻接顶点均已访问），再回溯到上一顶点，选择未访问的邻接顶点继续深入，重复此过程直至所有顶点被访问。

实现步骤（递归版）：

（1）访问起始顶点 v，标记为 “已访问”。

（2）遍历 v 的所有未访问邻接顶点 w，对每个 w 递归执行 DFS（即从 w 出发重复步骤 1-2）。

1、DFS 与树的先序遍历的相似性

（1）核心逻辑一致：“根（当前节点）优先，再深入分支”

树的先序遍历：访问根节点 → 依次先序遍历左子树 → 再先序遍历右子树（按子树顺序递归）。
图的 DFS：访问当前顶点 → 依次对该顶点的未访问邻接顶点执行 DFS（按邻接顺序递归）。

两者均体现 “先处理当前节点，再深入处理其 “子节点”（树的子树 / 图的邻接顶点）” 的顺序。

（2）递归结构相同：深度优先的递归探索

树的先序遍历通过递归深入左、右子树，直到叶子节点（无分支可走）。
图的 DFS 通过递归深入邻接顶点，直到所有邻接顶点均已访问（无未访问分支可走）。

两者的递归过程均呈现 “一路走到底，再回溯” 的深度优先特征。

2、DFS 的实现（突出与树先序的对比）

（1）数据结构与标记机制

树的先序遍历：无需标记（树无环，子树间无交叉，不会重复访问节点）。
图的 DFS：需用布尔数组 visited[] 标记顶点是否已访问（图可能有环或多路径，避免重复访问）。

（2）代码实现（以邻接表存储的无向图为例）

def dfs(graph, v, visited):# 1. 访问当前顶点（对应树的“访问根节点”）print(v, end=" ")visited[v] = True  # 标记为已访问（图特有的步骤）# 2. 遍历所有未访问的邻接顶点（对应树的“遍历子树”）# 邻接表中graph[v]是v的所有邻接顶点列表for w in graph[v]:if not visited[w]:dfs(graph, w, visited)  # 递归访问邻接顶点（对应树的递归子树）# 示例：无向图的邻接表（顶点0-3）
graph = [[1, 2],   # 0的邻接顶点：1, 2[0, 3],   # 1的邻接顶点：0, 3[0, 3],   # 2的邻接顶点：0, 3[1, 2]    # 3的邻接顶点：1, 2
]
visited = [False] * 4
print("DFS遍历序列：")
dfs(graph, 0, visited)  # 从顶点0出发
# 输出：0 1 3 2（与树先序遍历的“根→子树1→子树1的子树→子树2”逻辑一致）

3、与树先序遍历的关键差异

处理回路的机制：
- 树无环，先序遍历无需担心重复访问，递归自然终止（遇到叶子节点）。
- 图可能有环（如顶点 0-1-3-2-0），DFS 必须通过 visited 标记避免重复访问（否则递归会无限循环）。
“子节点” 的定义：
- 树的 “子节点” 是明确的（父节点唯一，子树有序），先序遍历按固定顺序（如左→右）访问。
- 图的 “邻接顶点” 无固定顺序（非父子关系），DFS 的遍历序列可能因邻接表的存储顺序不同而变化（但仍符合深度优先特征）。
适用范围：
- 树的先序遍历仅适用于树结构，目标是按 “根→子树” 顺序覆盖所有节点。
- DFS 适用于所有图（有向 / 无向、连通 / 非连通），除了遍历，还可用于检测环、求连通分量、拓扑排序等扩展场景。

4、示例对比：树的先序遍历 vs 图的 DFS

示例1：树的先序遍历（以二叉树为例）

    0/ \1   2\3

先序遍历序列：0 → 1 → 3 → 2（访问 0 → 先序 1 → 访问 1 → 先序 3 → 访问 3 → 回溯 → 先序 2 → 访问 2）。

示例2：图的 DFS（与树结构对应的图，无环）

0连接1、2；1连接3；3无其他连接

DFS 序列（从 0 出发）：0 → 1 → 3 → 2（与树先序完全一致，因无环且邻接顺序相同）。

示例3：图的 DFS（带环图）

0连接1、2；1连接3；3连接2；2连接0（形成环）

DFS 序列（从 0 出发）：0 → 1 → 3 → 2（因标记机制，即使有环也不会重复访问 0）。

例题1：

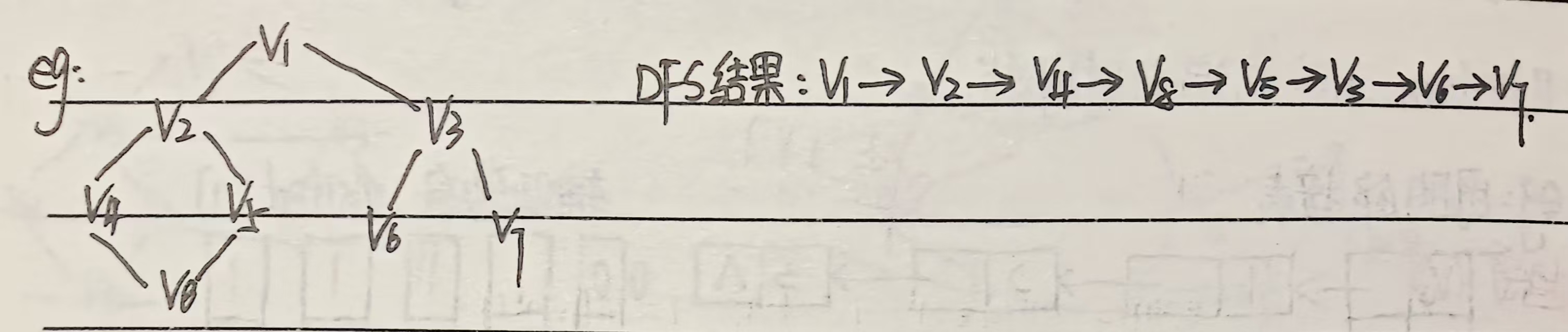
步骤：访问起始点 v ；若 v 的第1个邻接点没访问过，深度遍历此邻接点；若当前邻接点已访问过，再找 v 的第2个邻接点重新遍历，直至到达所有的邻接顶点都被访问过的 u 为止。然后退回到前一次刚访问过的顶点，进行DFS

例题2：

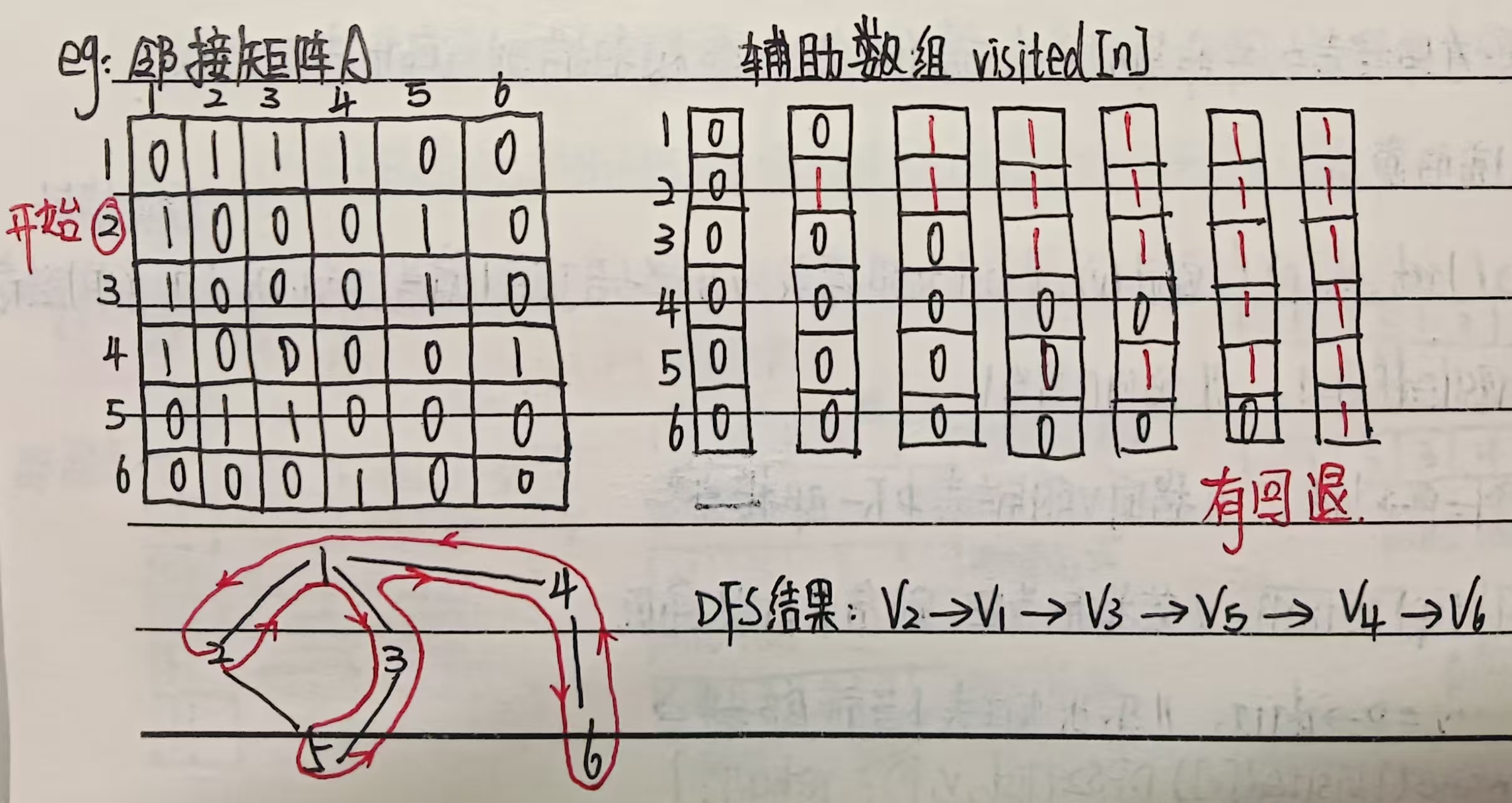
可用递归算法：

DFS1（A,n,v）
{visit(v); //A[n][n]为邻接矩阵，v 为起始顶点（编号），访问顶点 vvisited[v]=1; //访问过后修改辅助数组为1for(j=1;j<=n;j++) //从v所在行从头搜索邻接点if(A[v,j] && !visited[j]) //A[v,j]为1表示有邻接点，visited[j]为0表示未访问过DFS1(A,n,v);return;
}

建议：在递归函数中增加一计数器sum，初值为n，每访问一次就减1，减到0则return，可避免递归时间过长。

例题3：

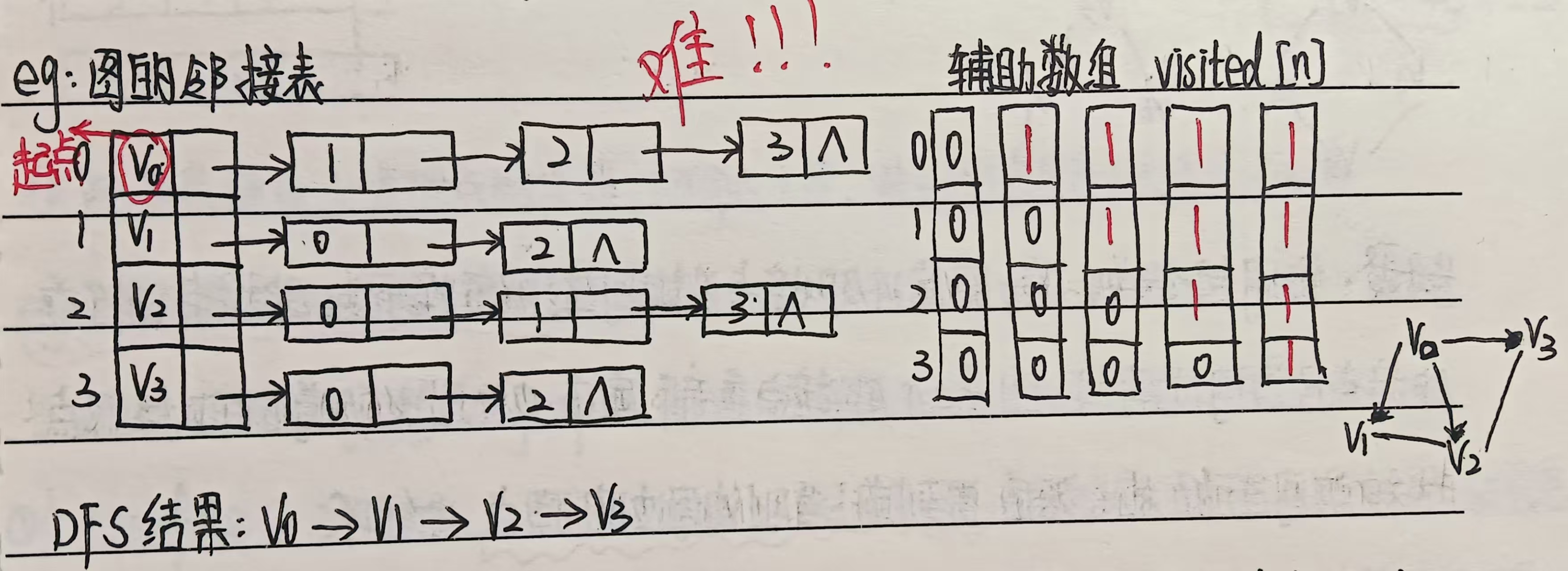
注意：在邻接表中，并非每个链表元素（即结点）都被扫描到，遍历速度很快。

可用递归算法：

DFS2(List,v,p)
{visit(v); //List为邻接表，v为起始顶点（编号），p为v所在那条单链表的头指针visited[v]=1; //访问后置为1p=p->link; //指向v的链表中下一邻接点if(ip) return; //若指针为空，则结束本次遍历v=p->data; //取出链表中当前邻接点while(!vixited[v])DFS2(list,v,p);return;
}