栈与队列:数据结构中的双雄对决
目录
一、栈
1.1概念及结构
1.2栈的实现
1.3栈的相关题
1.4栈的应用场景
二、队列
2.1队列的概念及结构
2.2队列的实现
2.3队列的相关题
2.4队列的应用场景
2.5环形队列扩展
设计环形队列
一、栈
1.1概念及结构
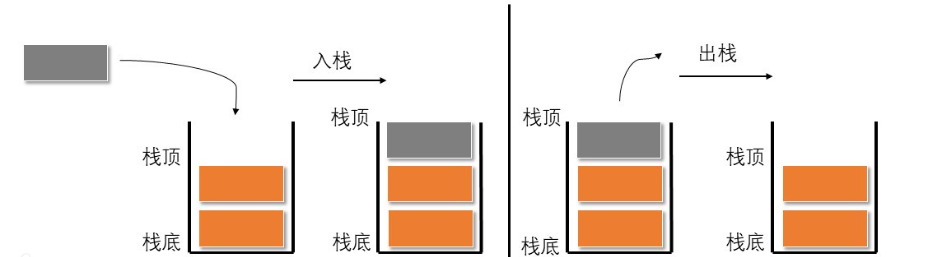
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶
出栈:栈的删除操作叫做出栈,出数据也在栈顶
在内存区域划分当中,也有栈,栈帧(Stack Frame) 是程序调用栈(Call Stack)中的一个关键结构,用于管理函数调用期间的局部数据、返回地址、参数传递等信息。每次函数被调用时,系统会在栈上为其分配一个栈帧;函数执行结束后,该栈帧被释放,栈顶恢复到调用前的状态。
栈在进程地址空间中的大小并非固定值,它取决于操作系统、硬件架构、系统配置以及程序的设置,通常在 几 MB 到几十 MB 之间
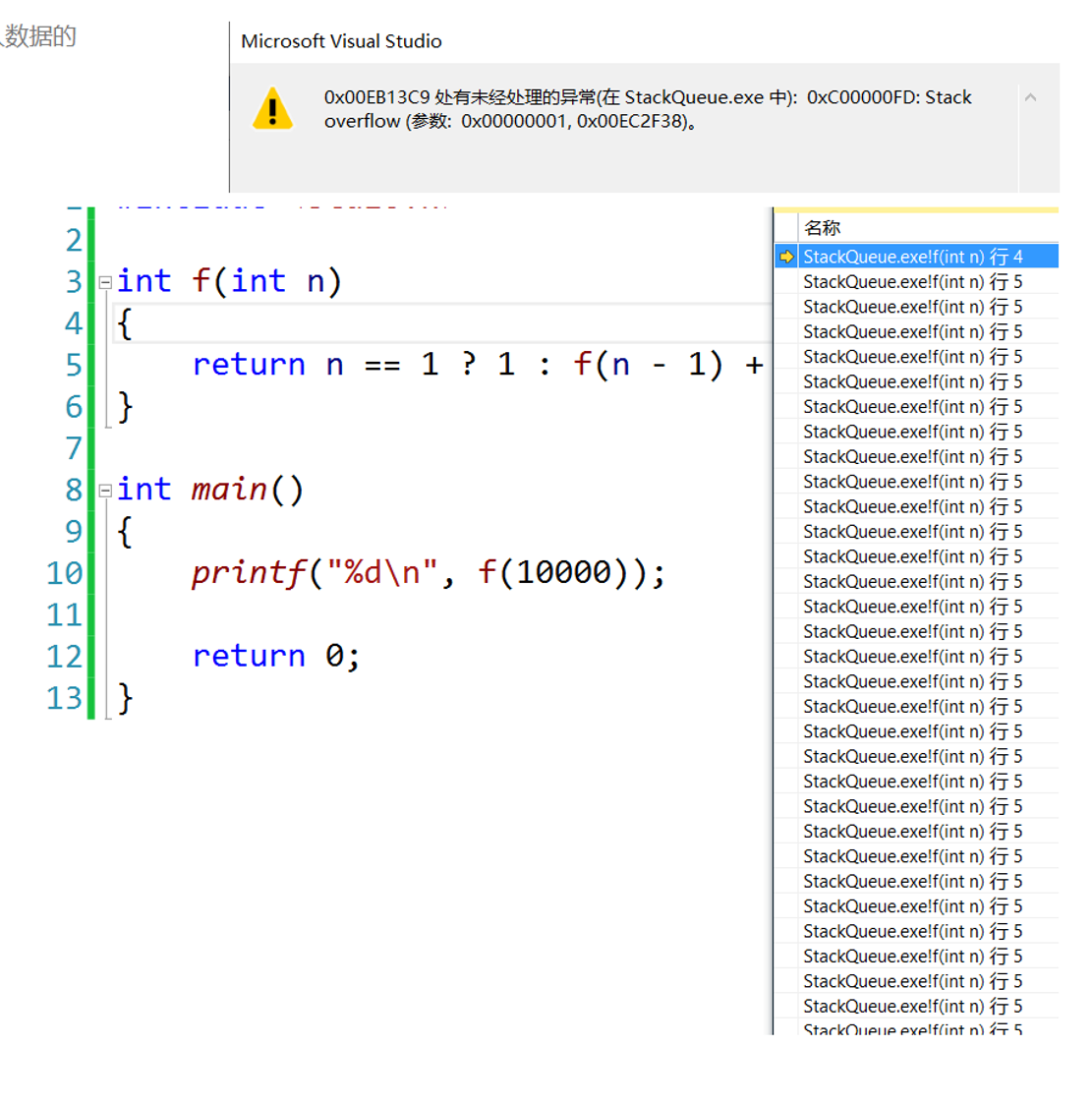
如果你写了一个递归函数,但是这个函数非常深,可能会导致栈溢出
1.2栈的实现
栈的实现一般可以使用数组或者链表来实现,相对而言,数组的结构实现更优一些,因为数组在尾上插入数据的代价比较小
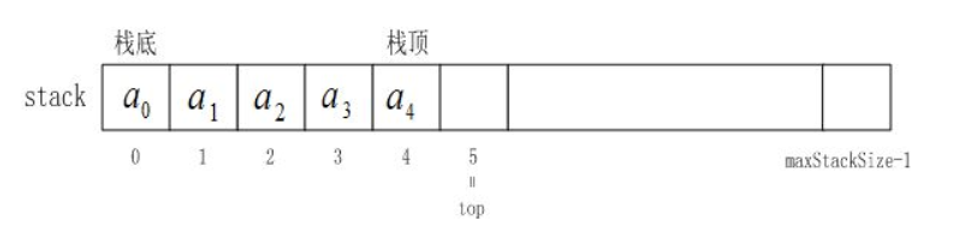
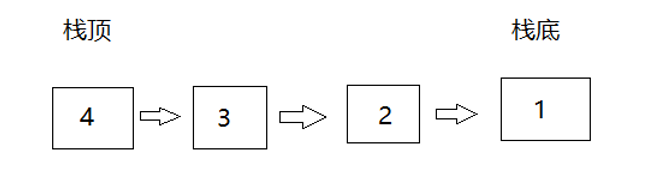
用数组尾插/尾删即可
用单链表实现栈的时候使用头插法头删法,否则尾插尾删时间复杂度为O(1)
如果要用尾插尾删法,需要双向链表,否则效率低
//#define N 100
//typedef int STDataType;
//struct Stack
//{
// STDataType a[N];
// int top;
//};typedef int STDataType;
typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);STDataType StackTop(ST* ps);
bool StackEmpty(ST* ps);
int StackSize(ST* ps);void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = ps->capacity = 0;
}void StackDestroy(ST* ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->capacity = ps->top = 0;
}void StackPush(ST* ps, STDataType x)
{assert(ps);// 扩容if (ps->top == ps->capacity){int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, newCapacity*sizeof(STDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}ps->a = tmp;ps->capacity = newCapacity;}ps->a[ps->top] = x;ps->top++;
}void StackPop(ST* ps)
{assert(ps);assert(!StackEmpty(ps));--ps->top;
}STDataType StackTop(ST* ps)
{assert(ps);assert(!StackEmpty(ps));return ps->a[ps->top - 1];
}bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}int StackSize(ST* ps)
{assert(ps);return ps->top;
}注意这里使用了realloc开辟空间,如果不适用tmp接收,使用原来的ps->a接受可能会导致返回null,从而导致找不到原来的那块空间而导致内存泄漏
这里使用了top作为栈顶的标记位,你在删除元素的时候,使用伪删除法,不是真的删除,只是修改了标记位,后来插入的元素可以覆盖
栈的实现很简单,只需要维护好后进先出的条件,开放一边端口(栈顶)作为操作口即可
1.3栈的相关题
1.有效的括号(leetcode20例题)
2.用栈实现队列(leetcode232例题)
1.4栈的应用场景
1.浏览器历史记录和编辑器的撤销动作
2.深度优先搜索
只要符合后进先出的特性都是可以用栈的
二、队列
2.1队列的概念及结构
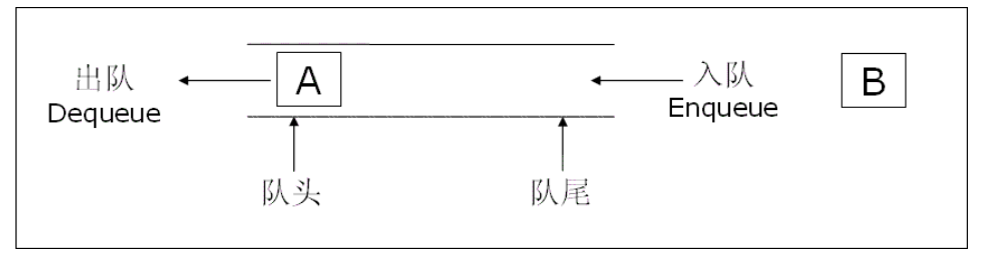
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
2.2队列的实现
队列的实现可以使用数组也可以使用链表,但是使用链表更优,因为数组在进行头删的时候效率很低,使用链表(单链表)需要维护一个尾指针标记尾结点,这样能够更好的尾插
typedef int QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);#include "Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);}pq->head = pq->tail = NULL;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}else{newnode->data = x;newnode->next = NULL;}if (pq->tail == NULL){pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);del = NULL;}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}int QueueSize(Queue* pq)
{assert(pq);/*QNode* cur = pq->head;int n = 0;while (cur){++n;cur = cur->next;}return n;*/return pq->size;
}2.3队列的相关题
1.用队列实现栈(leetcode225例题)(这里一个队列也能实现)
2.设计循环队列(leetcode622例题)
2.4队列的应用场景
只要是保证先进先出的特性的地方都可以用
1.进程/线程调度
2.生产者消费者模型
3.消息队列
4.比如生活当中银行医院的叫号,先拿号的先入队列,会被先叫到
2.5环形队列扩展
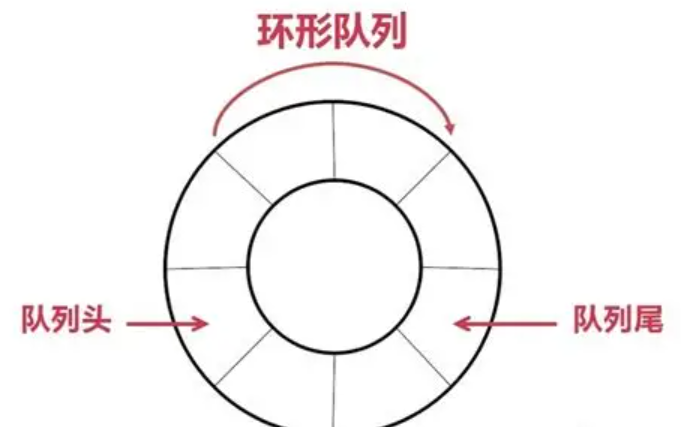
另外扩展了解一下,实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列可以使用数组实现,也可以使用循环链表实现。
环形队列(Circular Queue)是一种特殊的队列结构,通过将线性队列的首尾端相连,形成一个 “环形” 空间,解决了普通队列因频繁出队导致的内存浪费问题,提高了空间利用率。
是为了在 **“固定容量” 和 “高效访问”** 的场景下,优化普通数组队列的空间利用率和操作效率
因为你高效访问的话肯定是数组,但是数组如果前面出队列,后面入队列,效率很低,而且如果你想要效率高,就比如给数组前面标记,出队列,那头的位置就会更新成下一个下标,所以就会造成前面空间的浪费,为了找到高效访问和资源不浪费的下,设计环形队列
环形队列的核心价值不在于 “解决链表队列的问题”,而在于为固定容量、高效、实时的场景提供一种空间复用的数组队列实现。两者是互补而非替代关系,需根据具体需求选择。
设计环形队列
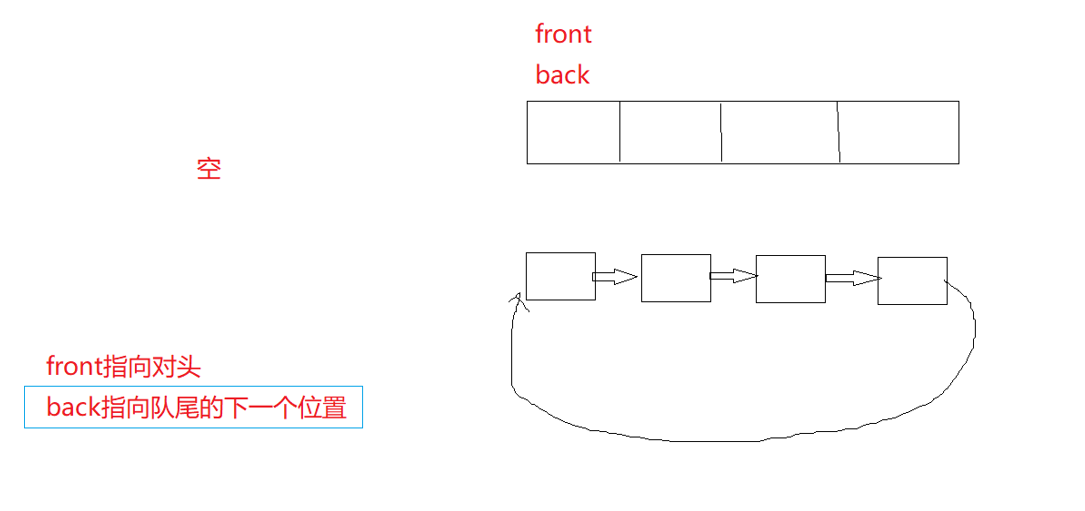
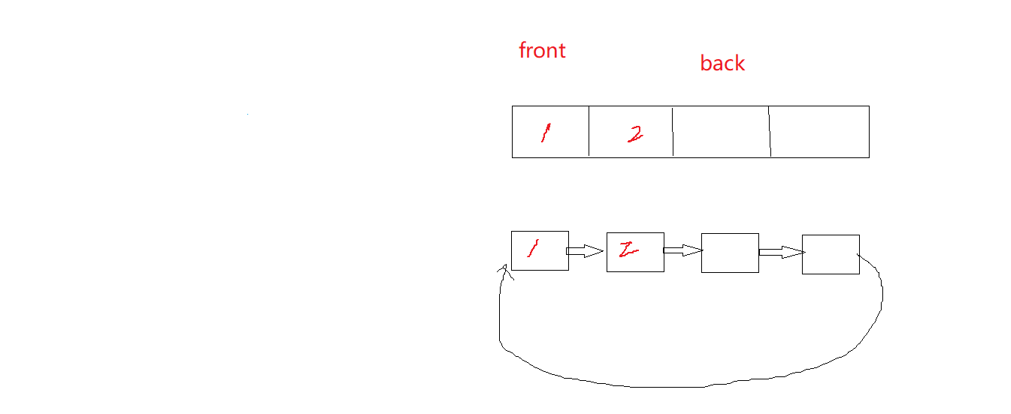
back永远是指向下一个要插入的位置
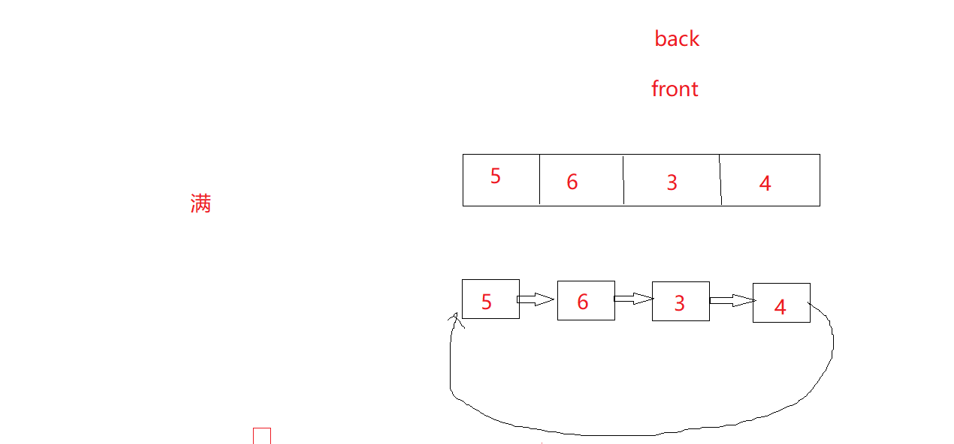
可以发现空的时候和满的时候,back和front都指向同一个位置?
那怎么区分什么时候是满?什么时候是空呢?
解决方法:
1.加一个size(如果front==back的时候,判断一个size即可)
2.增加一个空间,满的时候永远留一个位置,比如长度为4,就要开5个空间(此时back的下一个位置是front就是满)
