当前位置：首页 > news >正文

算法笔记 07

news 2025/10/22 9:44:14

1 递归就是出栈入栈？

递归的执行过程确实依赖于 “出栈” 和 “入栈” 操作，但不能简单地说 “递归就是出栈入栈”。两者的关系可以这样理解：

递归的执行过程本质是栈的操作当程序执行递归函数时，每次递归调用会触发一次 “入栈”：将当前函数的上下文（参数、局部变量、返回地址等）压入调用栈；当递归达到终止条件并开始返回时，会触发 “出栈”：从栈顶弹出上一层函数的上下文，恢复其执行状态。例如，计算 f(n) = f(n-1) + 1 时，调用 f(3) 会先入栈 f(3)，再入栈 f(2)、f(1)，直到终止条件后，依次弹出 f(1)、f(2)、f(3) 并计算结果。这个过程完全由 “入栈 - 出栈” 驱动。
递归的核心是逻辑，而非单纯的栈操作出栈入栈是递归的底层实现方式，但递归的本质是一种问题分解思想：通过将原问题拆解为更小的同类子问题，直到子问题可直接解决，再通过回溯合并结果。例如，二叉树的递归遍历，核心逻辑是 “先遍历左子树，再访问根节点，最后遍历右子树”，而栈操作只是编译器 / 解释器为实现这一逻辑所做的底层支持。
区别：自动管理 vs 手动操作递归中，出栈入栈由语言 runtime 自动完成，开发者无需关心栈的细节；而如果用栈手动模拟递归（如非递归遍历二叉树），则需要显式调用压栈、弹栈操作。这说明，栈操作是递归的实现手段，但递归本身是更高层次的抽象。

总结：递归的执行依赖出栈入栈操作，但递归的核心是 “自相似问题分解” 的逻辑，而非单纯的栈操作。可以说 “递归通过出栈入栈实现”，但不能将两者等同。

2 DFS（深度优先搜索Depth First Search）三部曲

要理解DFS（深度优先搜索）三部曲，我们可以结合C 语言二叉树的递归 DFS 遍历来拆解每一步，同时解答初学者的常见疑惑。

一、DFS 三部曲概述

DFS 的核心逻辑可归纳为 **“终止条件→选择与处理→回溯与撤销”三步，这三步构成了深度优先搜索的完整流程。下面结合二叉树的前序遍历（根 - 左 - 右）** 代码逐一解析。

二、代码示例（二叉树前序遍历，收集节点值）

先看一段 C 语言实现的二叉树前序遍历代码，再对应分析三部曲：

#include <stdio.h>
#include <stdlib.h>
#include <vector>
using namespace std;// 二叉树节点结构
typedef struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 存储结果的数组
vector<int> result;// DFS函数：前序遍历
void dfs(TreeNode* root) {// 1. 终止条件：当前节点为空，直接返回if (root == NULL) {return;}// 2. 选择与处理：访问当前节点（前序遍历先处理根）result.push_back(root->val);  // 将当前节点值加入结果// 3. 递归选择子节点（左→右），并隐含“回溯与撤销”dfs(root->left);   // 深入左子树dfs(root->right);  // 深入右子树// （此处无显式“撤销”，因为二叉树遍历是“一次性访问”，无需恢复节点状态）
}// 主函数：构建二叉树并测试
int main() {// 构建示例二叉树：根节点值为1，左子节点值为2，右子节点值为3TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));root->val = 1;root->left = (TreeNode*)malloc(sizeof(TreeNode));root->left->val = 2;root->left->left = NULL;root->left->right = NULL;root->right = (TreeNode*)malloc(sizeof(TreeNode));root->right->val = 3;root->right->left = NULL;root->right->right = NULL;dfs(root);  // 执行DFS前序遍历// 打印结果for (int val : result) {printf("%d ", val);  // 输出：1 2 3 }// 释放内存（省略，实际开发需注意）return 0;
}

三、逐步解析 DFS 三部曲

1. 终止条件

作用：定义递归何时停止，避免无限递归（栈溢出）。
对应代码：if (root == NULL) return;
初学者疑惑：
- “为什么终止条件是root == NULL？”因为二叉树的节点可能没有左 / 右子节点（即left或right指针为NULL），此时需要停止递归，否则会访问无效内存。
- “终止条件一定是节点为空吗？”不一定。比如 “找值为 5 的节点”，终止条件可以是root->val == 5（找到后返回结果）。终止条件由问题的结束场景决定。

2. 选择与处理

作用：处理当前节点的逻辑（如记录值、修改状态等），并选择 “下一个要深入的子节点”。
对应代码：result.push_back(root->val); + dfs(root->left); dfs(root->right);
初学者疑惑：
- “‘选择’具体指什么？”比如二叉树有左、右两个子节点，“选择左子节点” 就是决定先深入左子树。不同问题的 “选择” 不同，比如迷宫问题的 “上下左右四个方向”。
- “‘处理’必须在选择之前吗？”不一定。前序遍历是 “根 - 左 - 右”，所以先处理根；中序是 “左 - 根 - 右”，后序是 “左 - 右 - 根”—— 处理时机由遍历顺序（或问题需求）决定。

3. 回溯与撤销

作用：当从子节点回溯到当前节点时，撤销 “处理当前节点” 时的临时状态，让其他 “选择”（如右子节点）能在原始状态下执行。

对应代码：（二叉树遍历中无显式撤销，因为是 “单向访问”；但在需要 “恢复状态” 的场景会体现，如迷宫、全排列）

举个 全排列（C 语言简化版）的回溯例子，帮助理解 “撤销”：

#include <stdio.h>
#include <stdbool.h>
#define N 3int path[N];    // 存储当前排列
bool used[N];   // 标记元素是否已使用void dfs(int step) {// 终止条件：已选够N个元素if (step == N) {for (int i = 0; i < N; i++) {printf("%d ", path[i]);}printf("\n");return;}// 选择：遍历所有元素，选未使用的for (int i = 0; i < N; i++) {if (!used[i]) {// 处理：标记为已用，加入当前排列used[i] = true;path[step] = i + 1;  // 元素是1~Ndfs(step + 1);  // 深入下一层// 回溯与撤销：恢复状态，让其他选择可复用used[i] = false;// path[step] 无需显式撤销，因为下一次循环会覆盖}}
}int main() {dfs(0);return 0;
}

这里的used[i] = false;就是撤销操作—— 当从dfs(step + 1)回溯回来后，要把i标记为 “未使用”，这样其他分支（如i+1）才能选择它。

初学者疑惑：
- “什么时候需要‘回溯与撤销’？”当多个 “选择分支” 会共享同一份状态时，必须撤销。比如全排列中，“选 1 后再选 2” 和 “选 2 后再选 1” 是两个分支，需要恢复used数组的状态。而二叉树遍历中，每个节点的左、右子树是 “单向的”，访问后无需恢复，所以无显式撤销。

四、总结

DFS 三部曲是深度优先搜索的通用逻辑框架：

终止条件：定义递归的 “终点”，避免死循环。
选择与处理：执行当前节点的逻辑，并选择下一个要深入的子问题。
回溯与撤销：恢复当前节点的临时状态，保证其他分支的正确性。

3 BFS（广度优先搜索）

BFS（广度优先搜索）是与 DFS（深度优先搜索）并列的两种基础搜索算法，核心区别在于搜索顺序：DFS 是 “一条路走到底，不通再回头”（依赖栈或递归），而 BFS 是 “一层一层向外扩展”（依赖队列）。

下面结合二叉树的层序遍历（BFS 的典型应用），用 C 语言代码详细讲解 BFS 的逻辑、实现和常见疑问。

一、BFS 核心思想与适用场景

核心思想：从起点开始，先访问当前层的所有节点，再依次访问下一层的所有节点，像 “水波扩散” 一样逐层推进。
依赖的数据结构：队列（FIFO，先进先出），因为需要保证 “先访问的节点，其相邻节点也先被访问”。
适用场景：
- 二叉树的层序遍历（按层打印节点）；
- 最短路径问题（如无权图中找两点最短距离）；
- 迷宫问题（求最少步数走出迷宫）等。

二、BFS 与 DFS 的直观对比（以二叉树为例）

假设一棵二叉树结构如下：

    1/ \2   3/ \   \
4   5   6

DFS（前序遍历）：先深入左子树到底，再回溯处理右子树，顺序为 1 → 2 → 4 → 5 → 3 → 6；
BFS（层序遍历）：按 “层” 依次访问，顺序为 1 → 2 → 3 → 4 → 5 → 6（第 1 层：1；第 2 层：2、3；第 3 层：4、5、6）。

三、C 语言实现二叉树 BFS（层序遍历）

步骤拆解：

初始化队列：将根节点入队（起点）；
循环处理队列：每次取出队头节点，访问该节点；
扩展下一层：将当前节点的左、右子节点（若存在）依次入队；
终止条件：队列空时，所有节点访问完毕。

完整代码：

#include <stdio.h>
#include <stdlib.h>// 二叉树节点结构
typedef struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 队列节点结构（用于存储二叉树节点的指针）
typedef struct QueueNode {struct TreeNode *data;  // 存储二叉树节点struct QueueNode *next;
} QueueNode;// 队列结构（记录队头、队尾，方便入队/出队）
typedef struct {QueueNode *front;  // 队头（出队口）QueueNode *rear;   // 队尾（入队口）
} Queue;// 初始化队列
Queue* initQueue() {Queue *q = (Queue*)malloc(sizeof(Queue));q->front = q->rear = NULL;return q;
}// 入队操作（从队尾加入）
void enqueue(Queue *q, TreeNode *node) {QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->data = node;newNode->next = NULL;if (q->rear == NULL) {  // 队列空时，队头和队尾都指向新节点q->front = q->rear = newNode;} else {q->rear->next = newNode;  // 新节点接在队尾后q->rear = newNode;        // 更新队尾}
}// 出队操作（从队头取出）
TreeNode* dequeue(Queue *q) {if (q->front == NULL) return NULL;  // 队空，返回NULLQueueNode *temp = q->front;         // 暂存队头节点TreeNode *node = temp->data;        // 取出队头存储的二叉树节点q->front = q->front->next;          // 更新队头if (q->front == NULL) {             // 若队头为空，队尾也置空q->rear = NULL;}free(temp);  // 释放队列节点的内存return node;
}// 判断队列是否为空
int isEmpty(Queue *q) {return q->front == NULL;
}// BFS层序遍历函数
void bfs(TreeNode *root) {if (root == NULL) return;  // 空树直接返回Queue *q = initQueue();    // 初始化队列enqueue(q, root);          // 根节点入队（起点）while (!isEmpty(q)) {      // 队列不为空时循环TreeNode *current = dequeue(q);  // 取出队头节点printf("%d ", current->val);     // 访问当前节点（打印值）// 将左、右子节点入队（扩展下一层）if (current->left != NULL) {enqueue(q, current->left);}if (current->right != NULL) {enqueue(q, current->right);}}free(q);  // 释放队列（实际开发中需完整释放所有节点，此处简化）
}// 辅助函数：创建新节点
TreeNode* createNode(int val) {TreeNode *node = (TreeNode*)malloc(sizeof(TreeNode));node->val = val;node->left = node->right = NULL;return node;
}// 主函数：构建示例二叉树并测试
int main() {// 构建前文示例中的二叉树TreeNode *root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->right = createNode(6);printf("BFS层序遍历结果：");bfs(root);  // 输出：1 2 3 4 5 6 // 释放二叉树内存（省略，实际开发需递归释放）return 0;
}

四、关键细节与初学者常见疑问

1. 为什么 BFS 必须用队列，而 DFS 用栈？

BFS 的核心是 “逐层访问”：先访问的节点，其孩子节点属于下一层，需要 “后访问”，符合队列 “先进先出”（FIFO）的特性。例如先入队的根节点 1，出队后再入队其孩子 2、3，下次出队的就是 2、3（保证按层顺序）。
DFS 的核心是 “深入到底”：先访问的节点，其孩子节点需要 “先访问”，符合栈 “后进先出”（LIFO）的特性（递归本质是栈操作）。

2. 队列中存储的是什么？为什么要封装队列结构？

队列中存储的是二叉树节点的指针（TreeNode*），因为我们需要通过指针访问节点的左、右子节点。
封装队列结构（Queue）是为了方便管理入队、出队操作。如果直接用数组模拟队列，需要手动维护队头和队尾指针，逻辑类似但代码稍繁琐。

3. 入队时为什么要判断子节点是否为 NULL？

二叉树中，叶子节点的左 / 右子节点为NULL（如节点 4 的 left 和 right 都是 NULL）。如果将NULL入队，后续出队时访问NULL->val会导致空指针异常（程序崩溃），因此必须先判断子节点是否存在。

4. 如何按 “层” 输出（如单独打印每一层的节点）？

上述代码会连续打印所有节点，若要区分层次（如第 1 层：1；第 2 层：2 3；第 3 层：4 5 6），只需在循环中记录当前层的节点数量：

void bfsByLevel(TreeNode *root) {if (root == NULL) return;Queue *q = initQueue();enqueue(q, root);while (!isEmpty(q)) {int levelSize = 0;  // 当前层的节点数QueueNode *temp = q->front;// 计算当前层的节点数（队列中现有节点都是当前层的）while (temp != NULL) {levelSize++;temp = temp->next;}// 打印当前层的所有节点printf("第X层：");  // 实际可加变量记录层数for (int i = 0; i < levelSize; i++) {TreeNode *current = dequeue(q);printf("%d ", current->val);// 入队下一层节点if (current->left != NULL) enqueue(q, current->left);if (current->right != NULL) enqueue(q, current->right);}printf("\n");}free(q);
}

关键逻辑：每次循环开始时，队列中所有节点都属于 “当前层”，先统计数量，再依次出队并打印，同时入队下一层节点。

5. BFS 的时间复杂度和空间复杂度？

时间复杂度：O(n)（n为节点总数），每个节点入队和出队各一次，操作次数与节点数成正比。
空间复杂度：O(n)，最坏情况是 “满二叉树的最后一层”，节点数接近n/2，队列需存储这些节点。

五、BFS 与 DFS 的对比总结

维度	BFS（广度优先）	DFS（深度优先）
数据结构	队列	栈（或递归）
搜索顺序	逐层扩散	深入到底再回溯
适用场景	最短路径（无权图）、层序遍历	连通性判断、全排列、路径搜索
空间复杂度	取决于最宽层的节点数	取决于递归深度（树的高度）
实现难度	需手动管理队列，稍复杂	递归实现简洁，栈实现稍复杂

通过二叉树的层序遍历，能直观理解 BFS “按层扩展” 的核心逻辑。初学者可先掌握队列的基本操作，再结合具体场景（如迷宫最短路径）练习，逐步体会 BFS 的应用价值。

4 二叉堆

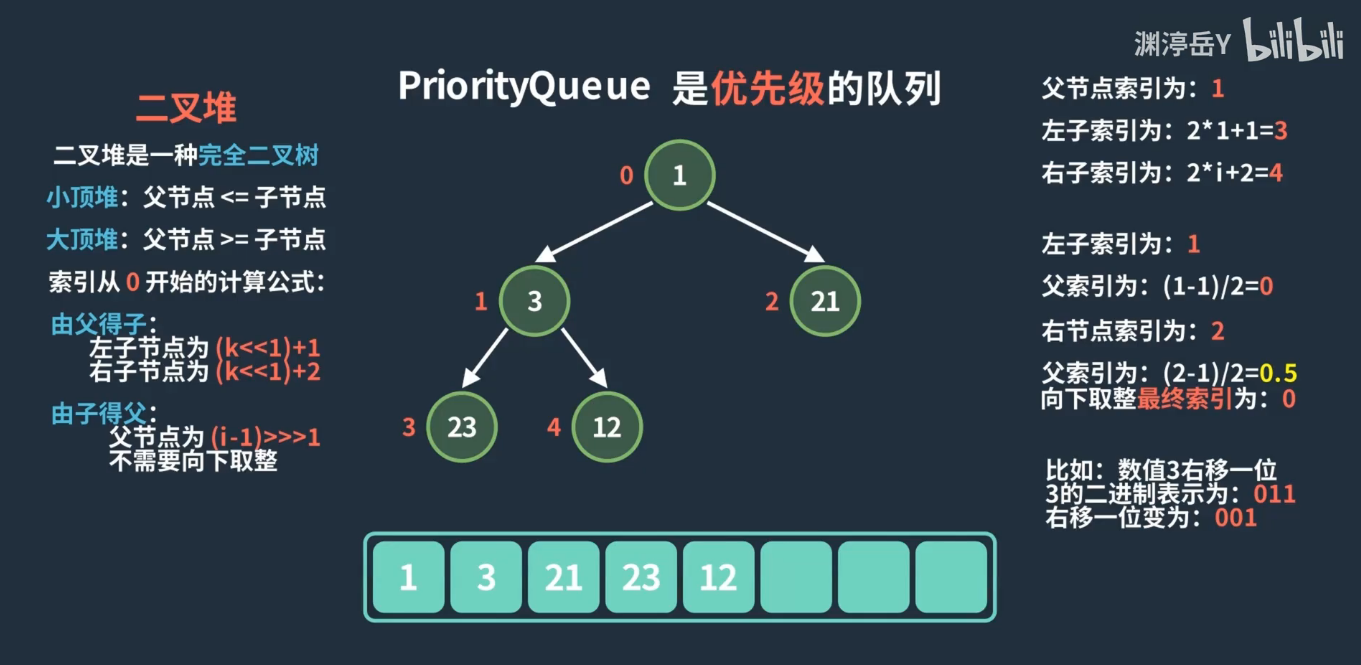
一、二叉堆的性质（结合存储与操作细节）

二叉堆是完全二叉树的数组实现，核心性质分为结构性质和堆序性质，二者共同决定了其高效操作的基础。

1. 结构性质（存储本质）

完全二叉树特性：除最后一层外，所有层节点全满；最后一层节点从左到右连续排列（无间隙）。这一特性允许用数组直接存储，无需指针：
- 根节点索引为 0
- 左子节点：2*i + 1
- 右子节点：2*i + 2
- 父节点：(i-1)/2（整数除法）
例：数组 [10,6,8,3,2,7] 对应完全二叉树：
plaintext
```
    10/   \6     8
/ \   /
```

3 2 7

plaintext

#### 2. 堆序性质（核心规则）
- **最大堆**：每个父节点 ≥ 子节点（堆顶为最大值）  
- **最小堆**：每个父节点 ≤ 子节点（堆顶为最小值）  ❗ 容易疑惑：堆序仅要求父节点与子节点的关系，**不要求左右子节点有序**（左子可大于/小于右子）。#### 3. 核心操作伪代码（以最大堆为例）
堆的操作本质是**破坏堆序后恢复平衡**，依赖两个核心函数：##### （1）向下调整（Heapify Down）
当堆顶元素被替换后，将新堆顶“下沉”到正确位置：
```plaintext
function heapify_down(heap, n, i):largest = i                // 假设当前节点最大left = 2*i + 1             // 左子节点索引right = 2*i + 2            // 右子节点索引if left < n and heap[left] > heap[largest]:largest = leftif right < n and heap[right] > heap[largest]:largest = rightif largest != i:           // 若子节点更大，交换并递归调整swap(heap[i], heap[largest])heapify_down(heap, n, largest)

❗ 疑惑点：n 是当前堆的大小（而非数组总长度），因为堆排序中会逐步缩小堆的范围。

（2）向上调整（Heapify Up）

插入新元素时，将元素 “上浮” 到正确位置：

plaintext

function heapify_up(heap, i):while i > 0:               // 未到根节点parent = (i-1)/2if heap[i] <= heap[parent]:  // 满足堆序，退出breakswap(heap[i], heap[parent])  // 否则与父节点交换i = parent

❗ 疑惑点：插入时先将元素放在数组末尾（完全二叉树的最后一个位置），再向上调整，保证结构性质不变。

二、最常见的应用：优先级队列

优先级队列的核心是 “按优先级访问元素”，二叉堆通过 O(log n) 的插入 / 提取操作实现高效调度。

1. 优先级队列的 C 语言实现（最大堆）

#include <stdio.h>
#include <stdlib.h>typedef struct {int* data;   // 存储堆的数组int size;    // 当前元素数量int capacity;// 最大容量
} PriorityQueue;// 初始化队列
PriorityQueue* initQueue(int capacity) {PriorityQueue* pq = (PriorityQueue*)malloc(sizeof(PriorityQueue));pq->data = (int*)malloc(sizeof(int) * capacity);pq->size = 0;pq->capacity = capacity;return pq;
}// 插入元素（入队）
void enqueue(PriorityQueue* pq, int val) {if (pq->size == pq->capacity) {printf("队列已满\n");return;}pq->data[pq->size] = val;  // 放在末尾heapify_up(pq->data, pq->size);  // 向上调整pq->size++;
}// 提取最大元素（出队）
int dequeue(PriorityQueue* pq) {if (pq->size == 0) {printf("队列为空\n");return -1;}int max = pq->data[0];             // 堆顶是最大值pq->data[0] = pq->data[pq->size-1];// 用最后一个元素替换堆顶pq->size--;heapify_down(pq->data, pq->size, 0);// 向下调整return max;
}// 向上调整（内部函数）
void heapify_up(int* heap, int i) {while (i > 0) {int parent = (i - 1) / 2;if (heap[i] <= heap[parent]) break;int temp = heap[i];heap[i] = heap[parent];heap[parent] = temp;i = parent;}
}// 向下调整（内部函数）
void heapify_down(int* heap, int n, int i) {while (1) {int largest = i;int left = 2*i + 1;int right = 2*i + 2;if (left < n && heap[left] > heap[largest]) largest = left;if (right < n && heap[right] > heap[largest]) largest = right;if (largest == i) break; // 无需调整int temp = heap[i];heap[i] = heap[largest];heap[largest] = temp;i = largest;}
}// 测试
int main() {PriorityQueue* pq = initQueue(10);enqueue(pq, 3);enqueue(pq, 5);enqueue(pq, 1);printf("%d ", dequeue(pq)); // 输出5printf("%d ", dequeue(pq)); // 输出3enqueue(pq, 6);printf("%d ", dequeue(pq)); // 输出6// 结果：5 3 6return 0;
}

2. 关键说明

入队流程：先追加元素，再通过 heapify_up 保证父节点 ≥ 子节点。
出队流程：取出堆顶后，用最后一个元素填补堆顶，再通过 heapify_down 恢复堆序。
❗ 疑惑点：优先级队列的 “队首” 永远是堆顶，无需维护整个队列的有序性，因此插入 / 出队效率远高于数组（O(n)）。

三、另一种应用：堆排序

堆排序利用最大堆（升序）或最小堆（降序）的特性，通过 “提取极值 + 调整堆” 实现排序，时间复杂度稳定为 O(n log n)。

1. 堆排序的 C 语言实现（升序）

#include <stdio.h>// 向下调整（同前，用于构建堆和排序）
void heapify_down(int* arr, int n, int i) {while (1) {int largest = i;int left = 2*i + 1;int right = 2*i + 2;if (left < n && arr[left] > arr[largest]) largest = left;if (right < n && arr[right] > arr[largest]) largest = right;if (largest == i) break;int temp = arr[i];arr[i] = arr[largest];arr[largest] = temp;i = largest;}
}// 构建最大堆
void build_max_heap(int* arr, int n) {// 从最后一个非叶子节点开始向前调整for (int i = (n-2)/2; i >= 0; i--) {heapify_down(arr, n, i);}
}// 堆排序（升序）
void heap_sort(int* arr, int n) {build_max_heap(arr, n);  // 第一步：构建最大堆for (int i = n-1; i > 0; i--) {// 交换堆顶（最大值）和当前堆尾int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 缩小堆范围，调整剩余元素为最大堆heapify_down(arr, i, 0);}
}// 测试
int main() {int arr[] = {3, 1, 4, 1, 5, 9};int n = sizeof(arr)/sizeof(arr[0]);heap_sort(arr, n);for (int i = 0; i < n; i++) {printf("%d ", arr[i]); // 输出：1 1 3 4 5 9}return 0;
}