Leetcode+Java+图论+最小生成树拓扑排序
53.寻宝
题目描述
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来(注意:这是一个无向图)。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述
输出联通所有岛屿的最小路径总距离
输入示例
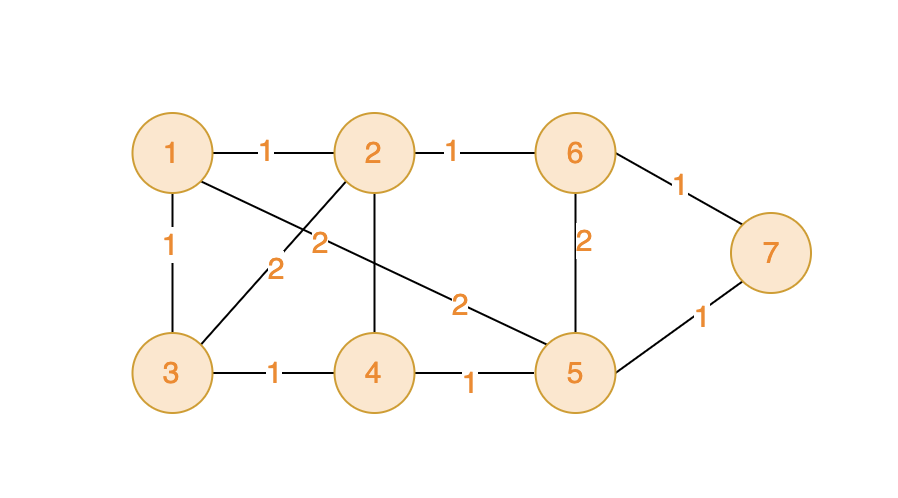
7 11 1 2 1 1 3 1 1 5 2 2 6 1 2 4 2 2 3 2 3 4 1 4 5 1 5 6 2 5 7 1 6 7 1输出示例
6提示信息
数据范围:
2 <= V <= 10000;
1 <= E <= 100000;
0 <= val <= 10000;如下图,可见将所有的顶点都访问一遍,总距离最低是6.
原理
Prim算法核心
从任意节点开始,逐步"生长"最小生成树:
text
1. 初始:选节点1,minDist[1]=0,其他=∞ 2. 迭代V-1次:a. 选未访问节点中minDist最小的cur,加入MSTb. 用cur更新所有未访问节点的距离 3. 总权 = Σ(minDist[2..V])
代码
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int V = scanner.nextInt(), E = scanner.nextInt();// minDist[i]:节点i到已选节点的最近距离,初始∞int[] minDist = new int[V + 1];Arrays.fill(minDist, 100001);// visited[i]:节点i是否已加入生成树boolean[] visited = new boolean[V + 1];// 邻接矩阵:grid[i][j] = i到j的边权,无边=∞int[][] grid = new int[V + 1][V + 1];for (int i = 1; i <= V; i++) Arrays.fill(grid[i], 100001);// 构建无向图邻接矩阵for (int i = 0; i < E; i++) {int u = scanner.nextInt(), v = scanner.nextInt(), k = scanner.nextInt();grid[u][v] = k; // u→vgrid[v][u] = k; // v→u(无向图)}// Prim算法:V-1次迭代构建MSTfor (int i = 1; i < V; i++) {// Step1:找未访问节点中minDist最小的curint cur = -1, minVal = Integer.MAX_VALUE;for (int j = 1; j <= V; j++) {if (!visited[j] && minDist[j] < minVal) {minVal = minDist[j];cur = j;}}visited[cur] = true; // 加入生成树// Step2:用cur更新所有未访问节点的距离for (int j = 1; j <= V; j++) {if (!visited[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j]; // 松弛操作}}}// 计算MST总权:除起点外所有节点的minDist之和int result = 0;for (int i = 2; i <= V; i++) {result += minDist[i];}System.out.print(result);}
}原理
Kruskal算法(版本1)
核心:贪心 + 并查集
text
1. 将所有边按权重从小到大排序 2. 从最小边开始依次添加:- 如果两端点不在同一连通分量 → 添加这条边- 否则 → 跳过(形成环) 3. 直到连通V-1条边,得到最小生成树
代码
import java.util.*;class Edge {int l, r, val; // 起点、终点、权重Edge(int l, int r, int val) { this.l = l; this.r = r; this.val = val; }
}public class Main {private static int n = 10001;private static int[] father = new int[n];// 初始化并查集public static void init() { for (int i = 0; i < n; i++) father[i] = i; }// 路径压缩查找public static int find(int u) {return u == father[u] ? u : (father[u] = find(father[u]));}// 合并集合public static void join(int u, int v) {u = find(u); v = find(v);if (u == v) return;father[u] = v; // 简单合并}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int V = scanner.nextInt(), E = scanner.nextInt();// 存储所有边List<Edge> edges = new ArrayList<>();for (int i = 0; i < E; i++) {int u = scanner.nextInt(), v = scanner.nextInt(), k = scanner.nextInt();edges.add(new Edge(u, v, k));}// 按权重排序(核心!)edges.sort(Comparator.comparing(edge -> edge.val));init(); // 初始化并查集int result = 0;// Kruskal算法:从小到大加边for (Edge edge : edges) {if (find(edge.l) != find(edge.r)) { // 不同集合才加result += edge.val; // 累加权重join(edge.l, edge.r); // 合并集合}}System.out.print(result);}
}117.软件构建
题目描述
某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
输入描述
第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。
后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
输出描述
输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
如果不能成功处理(相互依赖),则输出 -1。
输入示例
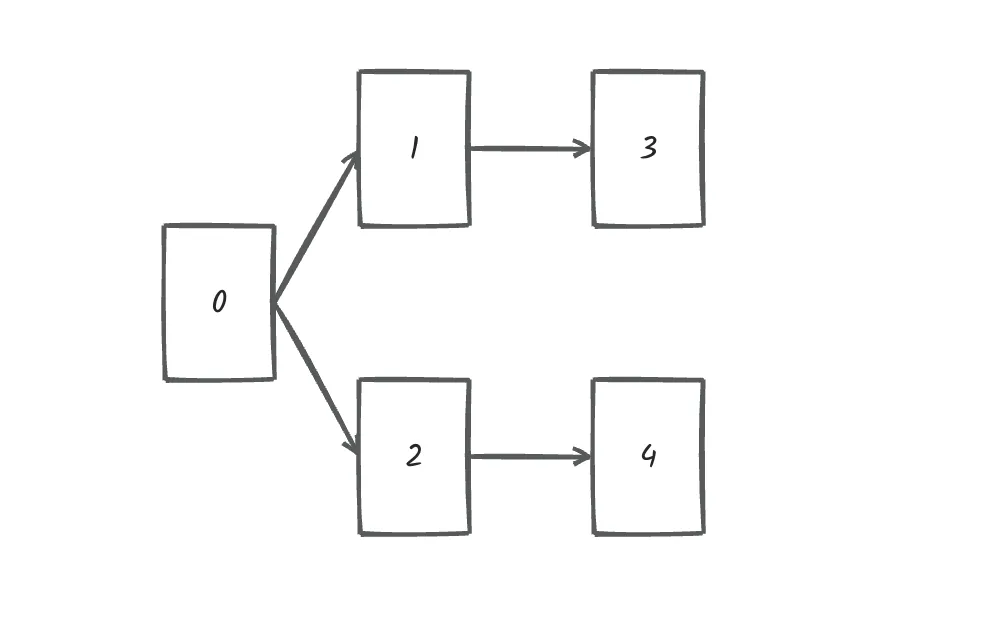
5 4 0 1 0 2 1 3 2 4输出示例
0 1 2 3 4提示信息
文件依赖关系如下:
所以,文件处理的顺序除了示例中的顺序,还存在
0 2 4 1 3
0 2 1 3 4
等等合法的顺序。
数据范围:
0 <= N <= 10 ^ 5
1 <= M <= 10 ^ 9
每行末尾无空格。
原理
Kahn算法(拓扑排序)
核心:入度为0 → 处理 → 减少依赖 → 重复
text
1. 初始:找所有入度=0的文件入队 2. 循环:a. 取出队首文件cur,加入结果b. cur处理完 → 减少其所有依赖文件的入度c. 新入度=0的文件入队 3. 结果长度==N → 成功;否则 → 存在环
代码
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int N = scanner.nextInt(); // 文件数int M = scanner.nextInt(); // 依赖关系数// 入度数组:inDegree[i] = 文件i的依赖数int[] inDegree = new int[N];// 邻接表:list[i] = 文件i依赖的文件列表List<List<Integer>> list = new ArrayList<>();for (int i = 0; i < N; i++) {list.add(new ArrayList<>());}// 构建图 + 计算入度for (int i = 0; i < M; i++) {int s = scanner.nextInt(); // s → t(t依赖s)int t = scanner.nextInt();list.get(s).add(t); // s依赖tinDegree[t]++; // t入度+1}// 标记数组:防止重复入队boolean[] flag = new boolean[N];// 队列:存储入度为0的节点(无依赖,可先处理)Queue<Integer> queue = new ArrayDeque<>();for (int i = 0; i < N; i++) {if (inDegree[i] == 0) {queue.add(i);flag[i] = true;}}// 结果拓扑排序List<Integer> result = new ArrayList<>();// Kahn算法:拓扑排序while (!queue.isEmpty()) {int cur = queue.poll(); // 取出当前文件result.add(cur); // 加入结果// 处理cur的所有依赖文件,入度-1for (int next : list.get(cur)) {inDegree[next]--;}// 重新扫描找新入度为0的节点for (int i = 0; i < N; i++) {if (!flag[i] && inDegree[i] == 0) {queue.add(i);flag[i] = true;}}}// 判断是否所有文件都处理完if (result.size() == N) {// 输出拓扑顺序for (int i = 0; i < N; i++) {if (i == 0) System.out.print(result.get(i));else System.out.print(" " + result.get(i));}} else {System.out.print(-1); // 存在环,无法排序}}
}