汽车MIMO雷达在多径环境下的角度估计——论文阅读

汽车MIMO雷达在多径环境下的角度估计

F. Engels, M. Wintermantel and P. Heidenreich, “Automotive MIMO radar angle estimation in the presence of multipath,” 2017 European Radar Conference (EURAD), Nuremberg, Germany, 2017, pp. 82-85

研究背景与动机

在现代汽车雷达系统中，MIMO（多输入多输出）技术被广泛应用以提升分辨率和信噪比性能。与传统相控阵雷达系统仅发射单一波形的缩放版本不同，MIMO雷达发射多个正交波形，这种波形多样性带来了更高的分辨率、更好的参数可识别性和信噪比性能改善。在汽车雷达应用中，特别是采用两个发射天线放置在接收阵列天线两侧的MIMO方案，可以有效地将物理阵列孔径加倍，从而在各种MIMO方案中提供最优的物理孔径与虚拟孔径比。

雷达能够在恶劣天气和光照条件下可靠工作，并能提供多个目标的距离、相对速度和角度的准确测量。作为当前先进驾驶辅助系统中的常用技术，雷达被认为是高度自动驾驶的关键技术之一。然而，在某些关键应用场景中，由于频率分辨率有限，传统处理方法会失效。这时需要对选定的处理单元应用具有高分辨率能力的基于模型的参数估计方法。

本研究重点关注角度域的参数估计，特别是实际相关的应用场景，包括通过护栏产生的水平多径，或者涉及高架目标（如桥梁或龙门标志）的垂直多径。在后一种情况下，除了传感器与目标之间的直接传播路径外，还存在通过路面的间接传播路径。

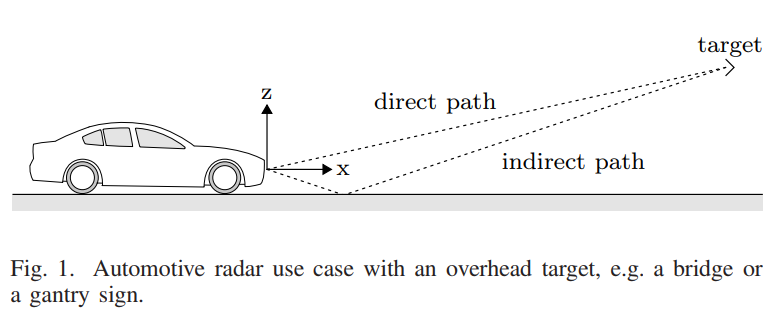
图1 - 汽车雷达垂直多径场景示意图：图中展示了一个典型的汽车雷达应用场景，其中包含一个高架目标（如桥梁或龙门标志）。图中用实线表示直接传播路径（direct path），虚线表示经由路面反射的间接传播路径（indirect path）。坐标系采用x轴表示水平距离，z轴表示垂直高度。这种几何配置清楚地说明了多径传播的物理机制：雷达信号不仅通过空气直接到达目标，还会先射向路面，经反射后到达目标，形成镜像效应。

在标准相控阵雷达中，这种情况对应于包含两个目标的信号模型，即实际目标和通过路面镜像的目标。如果目标之间的角度间隔低于分辨率限制，传统处理会产生错误的垂直位置估计，这可能导致严重的系统反应，例如不合理的紧急制动。为了应对这种情况，可以使用基于双目标模型的高分辨率角度估计。然而，当使用MIMO方案来合成增加阵列孔径时，标准的双目标信号模型不再有效，这就是本文要解决的核心问题。

MIMO雷达信号建模详解

基本MIMO信号模型的物理意义

考虑一个最先进的雷达传感器，它使用线性调频序列调制和MIMO处理。系统包含$N_t$个发射天线组成的均匀线性阵列（天线间距为$d_t$）和$N_r$个接收天线组成的均匀线性阵列（天线间距为$d_r$）。为了简化表示，我们考虑一维角度估计问题。

雷达预处理包括脉冲压缩、脉冲间傅里叶变换和功率检测。处理后的雷达数据根据距离和相对速度被划分到不同的处理单元中。当某个处理单元中存在单个目标时，无噪声的MIMO信号模型可以表示为：

$${\mathbf{x}}_1({\varphi }_1,s_1)=s_1[{\mathbf{a}}_t({\varphi }_1)\otimes {\mathbf{a}}_r({\varphi }_1)]=s_1\mathbf{v}({\varphi }_1)$$

其中Kronecker积$\otimes$的物理意义是将发射和接收阵列响应组合成一个虚拟阵列响应。参数${\varphi }_1$是电角度，$s_1$是目标响应参数（包含目标反射率和传播损耗等信息），$\mathbf{v}(\varphi )$是MIMO导向矢量。

发射和接收导向矢量的具体形式为：

$${\mathbf{a}}_t(\varphi )=[1,e^{j{\varphi }_t},e^{j2{\varphi }_t},...,e^{j(N_t-1){\varphi }_t}{]}^T$$

$${\mathbf{a}}_r(\varphi )=[1,e^{j{\varphi }_r},e^{j2{\varphi }_r},...,e^{j(N_r-1){\varphi }_r}{]}^T$$

这些导向矢量描述了平面波到达均匀线性阵列时各天线元素之间的相位关系。电角度与物理角度$\phi$的关系为：

$${\varphi }_t=\frac{2\pi }{\lambda }{d}_t\sin (\phi ),{\varphi }_r=\frac{2\pi }{\lambda }{d}_r\sin (\phi )$$

其中$\lambda$是雷达信号的波长。由于接收和发射阵列可能有不同的天线间距，我们定义统一的电角度关系：$\varphi ={\varphi }_r=\frac{d_r}{d_t}{\varphi }_t$。

双目标MIMO信号模型的扩展

当处理单元中存在两个目标时，接收信号是两个目标响应的线性叠加：

$$\begin{array}{rl}{\mathbf{x}}_2({\varphi }_1,{\varphi }_2,s_1,s_2)& =s_1[{\mathbf{a}}_t({\varphi }_1)\otimes {\mathbf{a}}_r({\varphi }_1)]+s_2[{\mathbf{a}}_t({\varphi }_2)\otimes {\mathbf{a}}_r({\varphi }_2)]\\ & =s_1\mathbf{v}({\varphi }_1)+s_2\mathbf{v}({\varphi }_2)\end{array}$$

这里${\varphi }_1$和${\varphi }_2$分别对应两个目标的电角度，$s_1$和$s_2$是相应的目标响应参数。这个模型假设两个目标是独立的散射体，它们的回波信号在接收端进行相干叠加。

多径环境下单目标MIMO信号模型的创新

与双目标模型根本不同的是，多径情况下的单目标信号包含四个传播路径组合，这是本文的核心创新。这四个分量分别对应于：

1. 直接/直接路径（$s_{11}$项）：发射信号直接到达目标，反射信号直接返回接收阵列
2. 直接/间接路径（$s_{12}$项）：发射信号直接到达目标，反射信号经路面反射返回接收阵列
3. 间接/直接路径（$s_{21}$项）：发射信号经路面反射到达目标，反射信号直接返回接收阵列
4. 间接/间接路径（$s_{22}$项）：发射信号和反射信号都经过路面反射

完整的多径信号模型表达式为：

$$\begin{array}{rl}{\mathbf{x}}_{mp}({\varphi }_1,{\varphi }_2,s_{11},s_{12},s_{21},s_{22})& =s_{11}[{\mathbf{a}}_t({\varphi }_1)\otimes {\mathbf{a}}_r({\varphi }_1)]\\ & +s_{12}[{\mathbf{a}}_t({\varphi }_1)\otimes {\mathbf{a}}_r({\varphi }_2)]\\ & +s_{21}[{\mathbf{a}}_t({\varphi }_2)\otimes {\mathbf{a}}_r({\varphi }_1)]\\ & +s_{22}[{\mathbf{a}}_t({\varphi }_2)\otimes {\mathbf{a}}_r({\varphi }_2)]\end{array}$$

这个模型可以用更紧凑的矩阵形式表示：

$${\mathbf{x}}_{mp}=\left([{\mathbf{a}}_t({\varphi }_1),{\mathbf{a}}_t({\varphi }_2)]\otimes [{\mathbf{a}}_r({\varphi }_1),{\mathbf{a}}_r({\varphi }_2)]\right)\left[\begin{array}{c}{s}_{11}\\ s_{12}\\ s_{21}\\ s_{22}\end{array}\right]$$

定义${\mathbf{A}}_t=[{\mathbf{a}}_t({\varphi }_1),{\mathbf{a}}_t({\varphi }_2)]$为发射阵列矩阵，${\mathbf{A}}_r=[{\mathbf{a}}_r({\varphi }_1),{\mathbf{a}}_r({\varphi }_2)]$为接收阵列矩阵，则有：

$${\mathbf{x}}_{mp}=({\mathbf{A}}_t\otimes {\mathbf{A}}_r)\mathbf{s}$$

其中$\mathbf{s}=[s_{11},s_{12},s_{21},s_{22}{]}^T$是包含所有路径响应参数的向量。

MIMO测量模型

实际测量中，所有信号模型都需要考虑噪声的影响。测量模型通过在理想信号模型${\mathbf{x}}_1$、${\mathbf{x}}_2$和${\mathbf{x}}_{mp}$上添加循环复高斯噪声获得：

$$\mathbf{x}={\mathbf{x}}_{\text{signal}}+\mathbf{n}$$

其中$\mathbf{n}\sim \mathcal{C}\mathcal{N}(0,{\sigma }^2\mathbf{I})$是均值为零、协方差矩阵为${\sigma }^2\mathbf{I}$的循环复高斯噪声。

最大似然参数估计算法

单目标情况的波束形成器

对于单目标模型，最大似然估计等价于最大化接收信号在导向矢量方向上的投影功率：

$${\hat{\varphi }}_1=\arg \underset{{\varphi }_1}{\max }|\mathbf{v}({\varphi }_1{)}^H\mathbf{x}{|}^2$$

这个代价函数对应于经典的波束形成器，其物理意义是寻找使接收信号功率最大的到达角。当$d_t/d_r=N_r$时，虚拟阵列具有均匀线性阵列结构，可以使用FFT算法高效计算所有可能角度的响应。

展开代价函数可得：

$$|\mathbf{v}({\varphi }_1{)}^H\mathbf{x}{|}^2={\mathbf{x}}^H\mathbf{v}({\varphi }_1)\mathbf{v}({\varphi }_1{)}^H\mathbf{x}={\mathbf{x}}^H{\mathbf{P}}_1({\varphi }_1)\mathbf{x}$$

其中${\mathbf{P}}_1({\varphi }_1)=\mathbf{v}({\varphi }_1)\mathbf{v}({\varphi }_1{)}^H$是秩1的投影矩阵。

双目标情况的子空间投影

双目标模型的最大似然估计需要在二维参数空间中搜索：

$$({\hat{\varphi }}_1,{\hat{\varphi }}_2)=\arg \underset{{\varphi }_1,{\varphi }_2}{\max }\Vert {\mathbf{P}}_2({\varphi }_1,{\varphi }_2)\mathbf{x}{\Vert }^2$$

投影矩阵${\mathbf{P}}_2$将接收信号投影到两个导向矢量张成的子空间上：

$${\mathbf{P}}_2=\mathbf{V}{\mathbf{V}}^{+},\mathbf{V}=[\mathbf{v}({\varphi }_1),\mathbf{v}({\varphi }_2)]$$

这里使用Moore-Penrose伪逆${\mathbf{V}}^{+}$来处理$\mathbf{V}$可能不是列满秩的情况（当两个角度非常接近时）。代价函数的物理意义是测量信号在双目标信号子空间中的能量。

多径情况的张量积投影

多径模型的最大似然估计具有特殊的结构：

$$({\hat{\varphi }}_1,{\hat{\varphi }}_2)=\arg \underset{{\varphi }_1,{\varphi }_2}{\max }\Vert {\mathbf{P}}_{mp}({\varphi }_1,{\varphi }_2)\mathbf{x}{\Vert }^2$$

多径投影矩阵具有张量积结构：

$${\mathbf{P}}_{mp}=({\mathbf{A}}_t\otimes {\mathbf{A}}_r)({\mathbf{A}}_t\otimes {\mathbf{A}}_r{)}^{+}={\mathbf{P}}_t\otimes {\mathbf{P}}_r$$

其中${\mathbf{P}}_t={\mathbf{A}}_t{\mathbf{A}}_t^{+}$和${\mathbf{P}}_r={\mathbf{A}}_r{\mathbf{A}}_r^{+}$分别是发射和接收阵列的投影矩阵。

对于实际系统中常见的$N_t=2$发射天线的情况，有一个重要的简化。由于${\mathbf{A}}_t$是$2\times 2$的满秩矩阵，因此${\mathbf{P}}_t={\mathbf{I}}_2$（2×2单位矩阵）。代价函数简化为：

$$\begin{array}{rl}\Vert {\mathbf{P}}_{mp}\mathbf{x}{\Vert }^2& ={\Vert ({\mathbf{I}}_2\otimes {\mathbf{P}}_r)\left[\begin{array}{c}{\mathbf{x}}_{t1}\\ {\mathbf{x}}_{t2}\end{array}\right]\Vert }^2\\ & ={\Vert \left[\begin{array}{cc}{\mathbf{P}}_r& 0\\ 0& {\mathbf{P}}_r\end{array}\right]\left[\begin{array}{c}{\mathbf{x}}_{t1}\\ {\mathbf{x}}_{t2}\end{array}\right]\Vert }^2\\ & =\Vert {\mathbf{P}}_r{\mathbf{x}}_{t1}{\Vert }^2+\Vert {\mathbf{P}}_r{\mathbf{x}}_{t2}{\Vert }^2\end{array}$$

这个结果表明，最优估计器忽略了发射阵列结构，而是对两个子阵列向量进行非相干组合。这一发现具有重要的实际意义，因为它简化了计算复杂度。

模型判决框架与检测算法

广义似然比检验（GLRT）

为了在不同信号模型之间进行选择，采用广义似然比检验框架。在最大似然框架下，GLRT代表了最优方法。简化形式的GLRT检验统计量通过使用确定的最大似然参数估计计算各模型的均方误差比值获得。

判决规则如下：

• 在信号模型${\mathbf{x}}_2$和${\mathbf{x}}_1$之间判决：$\frac{{\text{MSE}}_1}{{\text{MSE}}_2}>T_2$
• 在信号模型${\mathbf{x}}_{mp}$和${\mathbf{x}}_1$之间判决：$\frac{{\text{MSE}}_1}{{\text{MSE}}_{mp}}>T_{mp}$

均方误差的具体计算为：

$${\text{MSE}}_1=\Vert \mathbf{x}-{\mathbf{x}}_1({\hat{\varphi }}_1,{\hat{s}}_1){\Vert }^2=\Vert \mathbf{x}-{\hat{s}}_1\mathbf{v}({\hat{\varphi }}_1){\Vert }^2$$

$${\text{MSE}}_2=\Vert \mathbf{x}-{\mathbf{x}}_2({\hat{\varphi }}_1,{\hat{\varphi }}_2,{\hat{s}}_1,{\hat{s}}_2){\Vert }^2$$

$${\text{MSE}}_{mp}=\Vert \mathbf{x}-{\mathbf{x}}_{mp}({\hat{\varphi }}_1,{\hat{\varphi }}_2,{\hat{s}}_{11},{\hat{s}}_{12},{\hat{s}}_{21},{\hat{s}}_{22}){\Vert }^2$$

这里$T_2$和$T_{mp}$是根据所需的检测概率和虚警概率选择的阈值，典型值为12 dB。

实验验证与结果分析

实验系统配置

实验使用了大陆公司的量产汽车雷达传感器，具体系统参数如下：

参数	数值
中心频率	76.15 GHz
脉冲带宽	83 MHz
脉冲重复时间	34 μs
发射天线间距	53.2 mm
接收天线间距	8.9 mm
每脉冲采样数	256
脉冲数	512
发射天线数	2
接收天线数	6

注意发射和接收天线间距满足$d_t/d_r=6$的关系，因此通过MIMO处理获得12元均匀线性虚拟阵列，阵列孔径相比物理阵列扩大了一倍。

实验场景设置

实验考虑了典型的垂直多径场景。在龙门架上3.1米高度固定一个角反射器作为目标，雷达传感器安装在车辆上，高度为0.6米。传感器方向设置使得发射和接收阵列垂直排列（平行于z轴）。车辆从200米的x位置开始，以30 km/h的恒定速度接近角反射器。

预期只有基于多径模型的角度估计能够提供准确的定位并分辨直接和间接传播路径。

实验结果详细分析

图2 - 三种方法的笛卡尔坐标位置估计对比

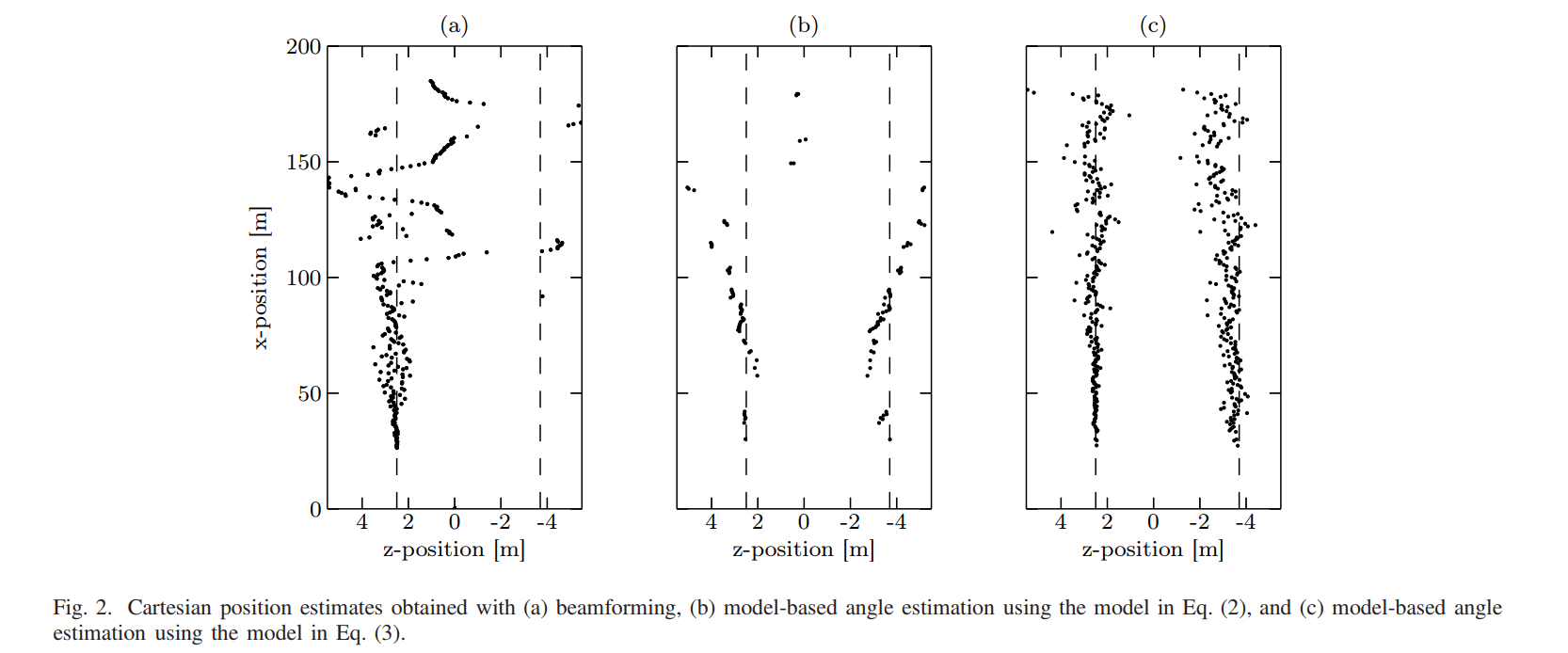
图2展示了使用三种不同方法获得的位置估计结果：

• 图2(a)显示了传统波束形成的结果
• 图2(b)显示了基于双目标模型的角度估计结果
• 图2©显示了基于多径模型的角度估计结果

每个子图中，横轴表示x方向的距离（0到200米），纵轴表示z方向的高度（-4到4米）。虚线垂直线标示了真实目标位置（3.1米高度）。

从图2(a)可以看出，波束形成结果显示出严重的垂直位置误差。在x距离大于50米时，估计的高度明显偏离真实值，呈现出一个向下弯曲的轨迹。只有当x距离小于50米时，直接路径才能被准确估计。这种现象可以解释为：当入射角较大时（远距离情况），间接信号分量由于路面反射系数的角度依赖性而衰减，导致估计偏向于间接路径。

图2(b)显示，基于双目标模型的角度估计在大多数距离上无法显著改善单目标模型的性能。只有在某些特定距离上（图中显示为离散的点），GLRT判决支持双目标模型，但估计结果仍然不够准确。

图2©清楚地表明，基于多径模型的角度估计成功地分离了直接和间接传播路径。在整个距离范围内，都能准确估计目标的真实高度（3.1米），同时也检测到了镜像目标（约-3.1米）。这验证了多径模型能够正确地描述物理传播机制。

图3 - GLRT检验统计量的经验分布

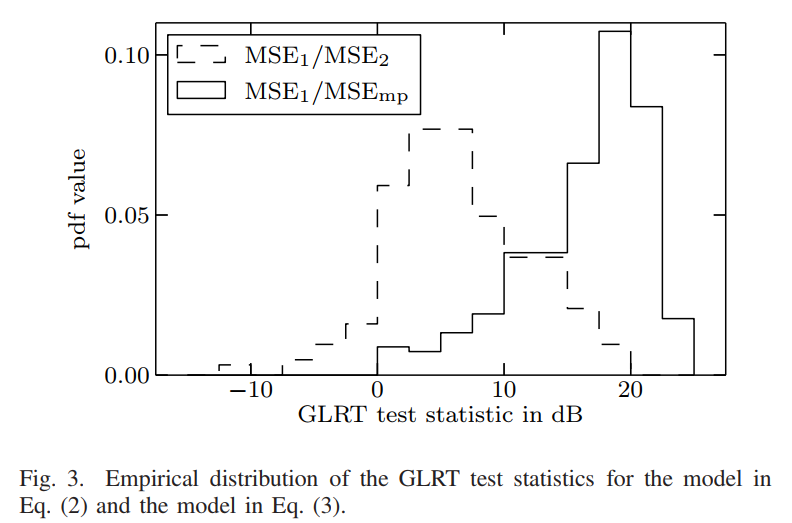
图3展示了两个GLRT检验统计量的概率密度函数（PDF）：

• 实线表示MSE₁/MSE₂的分布
• 虚线表示MSE₁/MSEₘₚ的分布

横轴是以dB为单位的GLRT检验统计量值（-10到20 dB），纵轴是概率密度值（0到0.10）。

从分布可以观察到，MSE₁/MSE₂的分布主要集中在0 dB附近，峰值约在-2 dB，这意味着双目标模型相比单目标模型只有边际改善。大部分值低于12 dB的判决阈值，表明在多数情况下，双目标模型不被选择。相比之下，MSE₁/MSEₘₚ的分布显示出明显不同的特征，其值普遍较大（主要分布在10-20 dB范围），远超过12 dB的阈值。这清楚地表明多径模型能够显著改善单目标模型，并且在统计意义上是更优的选择。

这两个分布的对比验证了理论分析：在多径环境下，传统的双目标模型不适用于MIMO雷达，而专门设计的多径模型能够正确描述信号传播特性。

结论与展望

本研究成功地将基于模型的角度估计扩展到汽车MIMO雷达的多径场景，这是该领域的一个重要进展。主要贡献包括：

首先，建立了适用于MIMO雷达多径传播的准确信号模型，该模型考虑了四种可能的传播路径组合，而不是简单地将多径情况视为双目标问题。这一创新性的建模方法正确地反映了MIMO系统中发射和接收阵列的联合效应。

其次，推导了相应的最大似然估计器，并发现了对于两发射天线系统的重要简化。这一简化不仅降低了计算复杂度，还提供了对MIMO处理本质的深刻理解：在多径情况下，最优处理策略是对子阵列进行非相干组合。

第三，提出了基于GLRT的模型选择框架，能够自动判别不同的信号场景。实验结果充分验证了理论分析，证明了该方法在实际系统中的有效性。

---

附录：数学推导

A. Kronecker积的性质与MIMO导向矢量推导

Kronecker积在MIMO信号模型中起着核心作用。对于两个矩阵$\mathbf{A}\in {\mathbb{C}}^{m\times n}$和$\mathbf{B}\in {\mathbb{C}}^{p\times q}$，其Kronecker积定义为：

$$\mathbf{A}\otimes \mathbf{B}=\left[\begin{array}{cccc}{a}_{11}\mathbf{B}& a_{12}\mathbf{B}& \cdots & a_{1n}\mathbf{B}\\ a_{21}\mathbf{B}& a_{22}\mathbf{B}& \cdots & a_{2n}\mathbf{B}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}\mathbf{B}& a_{m2}\mathbf{B}& \cdots & a_{mn}\mathbf{B}\end{array}\right]\in {\mathbb{C}}^{mp\times nq}$$

对于MIMO雷达系统，虚拟导向矢量通过发射和接收导向矢量的Kronecker积获得：

$$\mathbf{v}(\varphi )={\mathbf{a}}_t(\varphi )\otimes {\mathbf{a}}_r(\varphi )$$

展开这个表达式，对于$N_t=2$和$N_r=6$的情况：

$$\mathbf{v}(\varphi )=\left[\begin{array}{c}1\\ e^{j{\varphi }_t}\end{array}\right]\otimes \left[\begin{array}{c}1\\ e^{j{\varphi }_r}\\ e^{j2{\varphi }_r}\\ e^{j3{\varphi }_r}\\ e^{j4{\varphi }_r}\\ e^{j5{\varphi }_r}\end{array}\right]=\left[\begin{array}{c}1\\ e^{j{\varphi }_r}\\ e^{j2{\varphi }_r}\\ e^{j3{\varphi }_r}\\ e^{j4{\varphi }_r}\\ e^{j5{\varphi }_r}\\ e^{j{\varphi }_t}\\ e^{j({\varphi }_t+{\varphi }_r)}\\ e^{j({\varphi }_t+2{\varphi }_r)}\\ e^{j({\varphi }_t+3{\varphi }_r)}\\ e^{j({\varphi }_t+4{\varphi }_r)}\\ e^{j({\varphi }_t+5{\varphi }_r)}\end{array}\right]$$

当$d_t/d_r=6$时，有${\varphi }_t=6{\varphi }_r$，虚拟阵列变为均匀线性阵列：

$$\mathbf{v}(\varphi )=[1,e^{j{\varphi }_r},e^{j2{\varphi }_r},...,e^{j11{\varphi }_r}{]}^T$$

B. 最大似然估计的详细推导

B.1 单目标情况

给定含噪声的测量$\mathbf{x}=s_1\mathbf{v}({\varphi }_1)+\mathbf{n}$，其中$\mathbf{n}\sim \mathcal{C}\mathcal{N}(0,{\sigma }^2\mathbf{I})$，似然函数为：

$$p(\mathbf{x}|{\varphi }_1,s_1)=\frac{1}{(\pi {\sigma }^2{)}^{N_t{N}_r}}\exp \left(-\frac{1}{{\sigma }^2}\Vert \mathbf{x}-s_1\mathbf{v}({\varphi }_1){\Vert }^2\right)$$

对数似然函数为：

$$\mathcal{L}({\varphi }_1,s_1)=-N_t{N}_r\log (\pi {\sigma }^2)-\frac{1}{{\sigma }^2}\Vert \mathbf{x}-s_1\mathbf{v}({\varphi }_1){\Vert }^2$$

对$s_1$求导并令其为零：

$$\frac{\partial \mathcal{L}}{\partial s_1^{\ast }}=\frac{1}{{\sigma }^2}\mathbf{v}({\varphi }_1{)}^H(\mathbf{x}-s_1\mathbf{v}({\varphi }_1))=0$$

解得：

$${\hat{s}}_1=\frac{\mathbf{v}({\varphi }_1{)}^H\mathbf{x}}{\mathbf{v}({\varphi }_1{)}^H\mathbf{v}({\varphi }_1)}=\frac{\mathbf{v}({\varphi }_1{)}^H\mathbf{x}}{N_t{N}_r}$$

将${\hat{s}}_1$代入似然函数，得到压缩似然函数：

$$\mathcal{L}({\varphi }_1)=-N_t{N}_r\log (\pi {\sigma }^2)-\frac{1}{{\sigma }^2}\left(\Vert \mathbf{x}{\Vert }^2-\frac{|\mathbf{v}({\varphi }_1{)}^H\mathbf{x}{|}^2}{N_t{N}_r}\right)$$

最大化似然函数等价于最大化：

$$|\mathbf{v}({\varphi }_1{)}^H\mathbf{x}{|}^2$$

B.2 多径情况的张量积性质证明

对于多径投影矩阵：

$${\mathbf{P}}_{mp}=({\mathbf{A}}_t\otimes {\mathbf{A}}_r)[({\mathbf{A}}_t\otimes {\mathbf{A}}_r{)}^H({\mathbf{A}}_t\otimes {\mathbf{A}}_r){]}^{-1}({\mathbf{A}}_t\otimes {\mathbf{A}}_r{)}^H$$

利用Kronecker积的性质：

• $(\mathbf{A}\otimes \mathbf{B}{)}^H={\mathbf{A}}^H\otimes {\mathbf{B}}^H$
• $(\mathbf{A}\otimes \mathbf{B})(\mathbf{C}\otimes \mathbf{D})=\mathbf{AC}\otimes \mathbf{BD}$
• $(\mathbf{A}\otimes \mathbf{B}{)}^{-1}={\mathbf{A}}^{-1}\otimes {\mathbf{B}}^{-1}$（当$\mathbf{A}$和$\mathbf{B}$可逆时）

可以推导：

$$\begin{array}{rl}{\mathbf{P}}_{mp}& =({\mathbf{A}}_t\otimes {\mathbf{A}}_r)[({\mathbf{A}}_t^H{\mathbf{A}}_t)\otimes ({\mathbf{A}}_r^H{\mathbf{A}}_r){]}^{-1}({\mathbf{A}}_t^H\otimes {\mathbf{A}}_r^H)\\ & =({\mathbf{A}}_t\otimes {\mathbf{A}}_r)[({\mathbf{A}}_t^H{\mathbf{A}}_t{)}^{-1}\otimes ({\mathbf{A}}_r^H{\mathbf{A}}_r{)}^{-1}]({\mathbf{A}}_t^H\otimes {\mathbf{A}}_r^H)\\ & =[{\mathbf{A}}_t({\mathbf{A}}_t^H{\mathbf{A}}_t{)}^{-1}{\mathbf{A}}_t^H]\otimes [{\mathbf{A}}_r({\mathbf{A}}_r^H{\mathbf{A}}_r{)}^{-1}{\mathbf{A}}_r^H]\\ & ={\mathbf{P}}_t\otimes {\mathbf{P}}_r\end{array}$$

这证明了多径投影矩阵的张量积结构。

B.3 两发射天线情况的简化推导

当$N_t=2$时，${\mathbf{A}}_t\in {\mathbb{C}}^{2\times 2}$：

$${\mathbf{A}}_t=\left[\begin{array}{cc}1& 1\\ e^{j{\varphi }_{t1}}& e^{j{\varphi }_{t2}}\end{array}\right]$$

当${\varphi }_{t1}\ne {\varphi }_{t2}$时，${\mathbf{A}}_t$是满秩的，因此：

$${\mathbf{P}}_t={\mathbf{A}}_t({\mathbf{A}}_t^H{\mathbf{A}}_t{)}^{-1}{\mathbf{A}}_t^H={\mathbf{A}}_t{\mathbf{A}}_t^{-1}({\mathbf{A}}_t^H{)}^{-1}{\mathbf{A}}_t^H={\mathbf{I}}_2$$

这导致：

$${\mathbf{P}}_{mp}={\mathbf{I}}_2\otimes {\mathbf{P}}_r=\left[\begin{array}{cc}{\mathbf{P}}_r& 0\\ 0& {\mathbf{P}}_r\end{array}\right]$$

对于分块向量$\mathbf{x}=[{\mathbf{x}}_{t1}^T,{\mathbf{x}}_{t2}^T{]}^T$：

$$\Vert {\mathbf{P}}_{mp}\mathbf{x}{\Vert }^2={\Vert \left[\begin{array}{c}{\mathbf{P}}_r{\mathbf{x}}_{t1}\\ {\mathbf{P}}_r{\mathbf{x}}_{t2}\end{array}\right]\Vert }^2=\Vert {\mathbf{P}}_r{\mathbf{x}}_{t1}{\Vert }^2+\Vert {\mathbf{P}}_r{\mathbf{x}}_{t2}{\Vert }^2$$

C. GLRT检验统计量的分布推导

在噪声假设$\mathbf{n}\sim \mathcal{C}\mathcal{N}(0,{\sigma }^2\mathbf{I})$下，均方误差服从缩放的卡方分布。

对于单目标模型，残差为：
$${\mathbf{e}}_1=\mathbf{x}-{\hat{\mathbf{x}}}_1=(\mathbf{I}-{\mathbf{P}}_1)\mathbf{x}$$

其中${\mathbf{P}}_1=\mathbf{v}({\hat{\varphi }}_1)\mathbf{v}({\hat{\varphi }}_1{)}^H/(N_t{N}_r)$是秩1投影矩阵。

均方误差：
$${\text{MSE}}_1=\Vert {\mathbf{e}}_1{\Vert }^2={\mathbf{x}}^H(\mathbf{I}-{\mathbf{P}}_1{)}^2\mathbf{x}={\mathbf{x}}^H(\mathbf{I}-{\mathbf{P}}_1)\mathbf{x}$$

由于$(\mathbf{I}-{\mathbf{P}}_1)$是秩$(N_t{N}_r-1)$的投影矩阵，在零假设下：
$$\frac{{\text{MSE}}_1}{{\sigma }^2}\sim {\chi }_{2(N_t{N}_r-1)}^2$$

类似地，对于双目标和多径模型：
$$\frac{{\text{MSE}}_2}{{\sigma }^2}\sim {\chi }_{2(N_t{N}_r-2)}^2,\frac{{\text{MSE}}_{mp}}{{\sigma }^2}\sim {\chi }_{2(N_t{N}_r-4)}^2$$

因此，GLRT统计量的分布可以表示为F分布的函数：
$$\frac{{\text{MSE}}_1/{\text{MSE}}_2-1}{(N_t{N}_r-1)/(N_t{N}_r-2)-1}\sim F_{2,2(N_t{N}_r-2)}$$

这为阈值选择提供了理论依据。