【论文精度-3】POMO：强化学习中具有多个最优解的策略优化方法（Yeong-Dae Kwon 2020）

论文地址：

https://arxiv.org/abs/2010.16011https://arxiv.org/abs/2010.16011代码地址：

https://github.com/yd-kwon/POMOhttps://github.com/yd-kwon/POMO

这篇论文《POMO: Policy Optimization with Multiple Optima for Reinforcement Learning》是三星 SDS 团队在 2020 年 NeurIPS 上发表的一篇工作，主要针对组合优化（Combinatorial Optimization, CO）问题的深度强化学习（Deep Reinforcement Learning, DRL）求解方法进行了改进。

---

🧩 一、研究背景与问题动机

组合优化问题（如旅行商问题 TSP、车辆路径问题 CVRP、背包问题 KP）在物流、制造、调度等领域广泛存在。这类问题往往是 NP-hard 的，传统运筹优化算法（如启发式搜索、分支限界等）需要大量领域知识和人工设计。

近年来，强化学习（RL）在此类问题上表现出很强潜力，但现有方法（如 Pointer Network + REINFORCE、Attention Model 等）仍存在以下问题：

1. 存在多个等价最优解（symmetry）
   例如在 TSP 中，路径 (v1, v2, v3, v4, v5) 和 (v2, v3, v4, v5, v1) 表示相同的最优解，但传统训练仅学习其中一种表示，容易导致模型收敛到局部最优。

2. 高方差梯度与训练不稳定
   基于 REINFORCE 的方法依赖单一基线（baseline），方差大、收敛慢。

3. 推理阶段效率与精度权衡
   通常使用采样（sampling）或贪心（greedy）推理，但采样法慢、贪心法不稳定。

---

🚀 二、POMO 方法核心思想

POMO（Policy Optimization with Multiple Optima）的关键创新是：
在训练与推理阶段同时利用“多个等价最优解”的对称性信息，从多个起点并行优化策略。

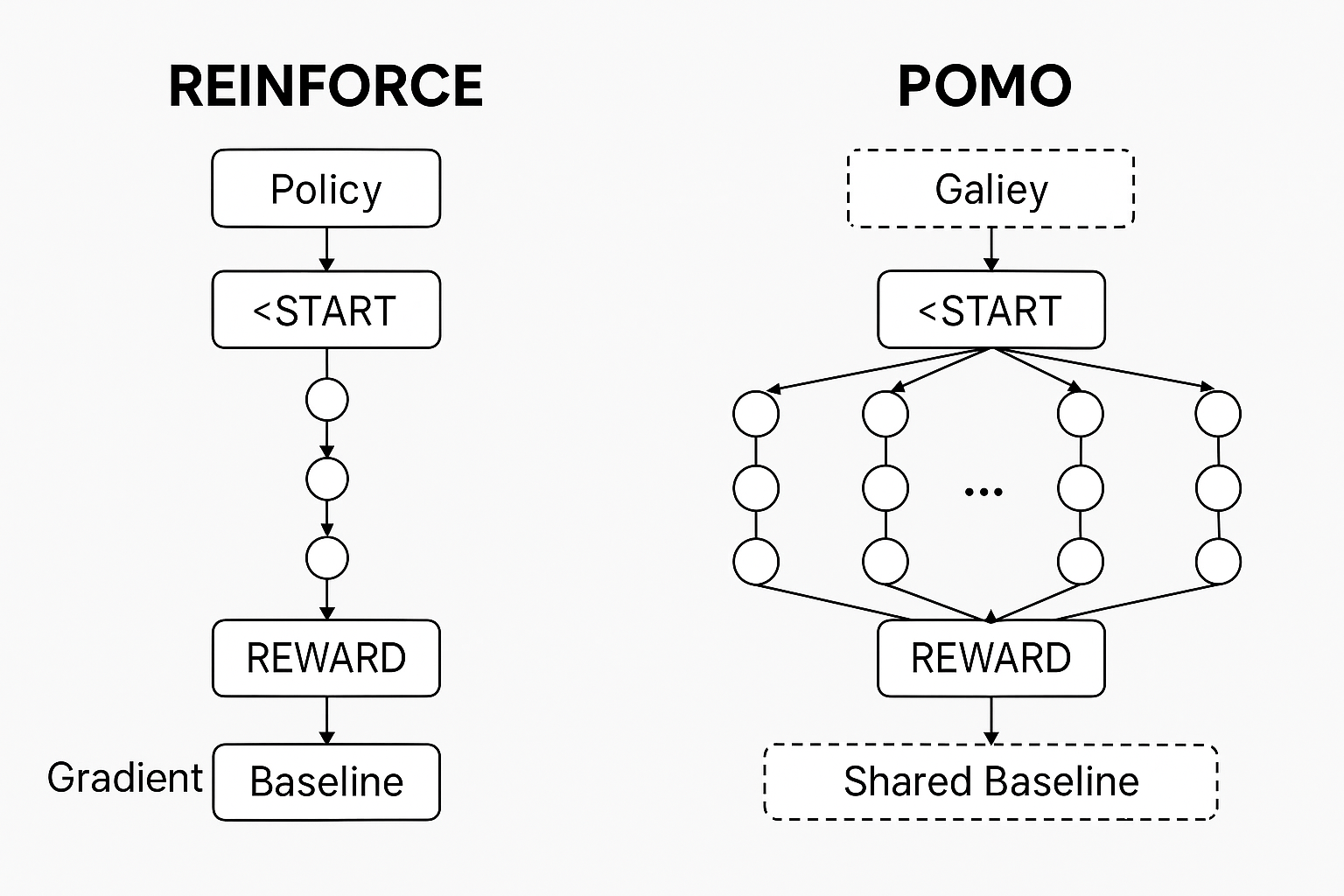
（1）多起点并行探索（Explorations from Multiple Starting Nodes）

传统模型通过一个 <START> token 生成单一路径；
POMO 则从 N 个不同起始节点 同时生成 N 条轨迹（trajectory）。

• 每个轨迹对应一种最优解的等价表示；

• 所有轨迹并行参与梯度更新；

• 通过“多视角学习”提升探索性与稳定性。

这相当于让模型从多个角度理解问题结构，避免只偏向单一路径。

---

（2）共享基线（Shared Baseline）以降低方差

POMO 基于 REINFORCE，但采用了共享基线（shared baseline）：

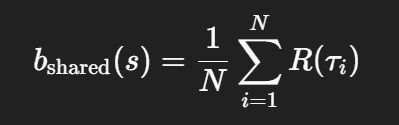
即所有 N 条轨迹的平均回报作为基线。

优点：

• 方差更小，梯度估计更稳定；

• 不依赖单独的 Critic 网络；

• 避免陷入局部最优（local minima）。

这相比传统的 greedy-rollout baseline 更快收敛、对初始化敏感性低。

---

（3）推理阶段：多贪心轨迹与实例增强（Inference with Multiple Greedy Trajectories & Augmentation）

推理时，POMO 不是只输出一个贪心轨迹，而是：

• 从 N 个起点生成 N 条贪心轨迹；

• 选取最优结果。

此外，引入Instance Augmentation（实例增强）：

• 对问题实例施加对称变换（如坐标翻转、旋转）；

• 在每个增强实例上独立推理；

• 取最优结果。

这一思想类似于图像识别中的“多视角评估”，可在不增加训练开销的情况下显著提升结果质量。

---

🧠 三、实验与结果分析

论文验证了 POMO 在三个经典组合优化问题上的表现：

1️⃣ Traveling Salesman Problem (TSP)

• 对比对象：Concorde、LKH3、Gurobi、Attention Model 等；

• POMO 在 TSP100 上的最优性差距仅 0.14%，推理速度快一个数量级。

• 同一 Attention Model 网络，换用 POMO 训练后，TSP100 最优性差距从 3.51% 降到 1.07%。

2️⃣ Capacitated Vehicle Routing Problem (CVRP)

• POMO 仍显著优于基线，CVRP100 的 gap 仅 0.32%；

• 即使不引入额外的“起点选择”模块（SelectStartNodes），也能有效利用对称性。

3️⃣ 0–1 Knapsack Problem (KP)

• 表明 POMO 并不限于路径类问题；

• 同样的网络结构，仅替换输入含义（weight, value），仍获得接近最优解。

---

🔍 四、优点与贡献总结

POMO 的贡献主要体现在三方面：

创新点	具体内容	效果
1. 多起点并行优化	充分利用组合优化问题的多重对称最优性	增强探索性与鲁棒性
2. 共享低方差基线	用全局平均回报代替单轨迹基线	训练稳定且收敛更快
3. 多贪心推理 + 实例增强	多视角决策、数据增强	精度显著提升，推理更快

---

🧮 五、总体结论

POMO 是一种通用的强化学习框架，能在不依赖人工启发式设计的情况下，自动学习高质量的组合优化求解策略。其优势包括：

• 纯数据驱动：无需手工规则；

• 快速稳定训练：低方差更新；

• 更优推理效果：借助对称性实现多最优学习；

• 广泛适用性：可扩展至 TSP、CVRP、KP 等多类问题。

🧭 六、POMO 的马尔可夫特性（Markov Property in POMO）

（1）基本概念回顾

在强化学习（RL）中，环境被形式化为一个马尔可夫决策过程（MDP），由五元组 (S,A,P,R,γ) 定义：

• S：状态空间（state space）

• A：动作空间（action space）

• P(s′∣s,a)：状态转移概率

• R(s,a)：即时奖励

• γ：折扣因子

马尔可夫性质（Markov Property） 表示系统的未来状态只依赖于当前状态和当前动作，而与过去历史无关。

---

（2）在 POMO 中的体现

POMO 仍然遵循马尔可夫性质，只是对传统强化学习的轨迹采样方式进行了改造。

在传统的 REINFORCE 框架下，生成轨迹的方式为：

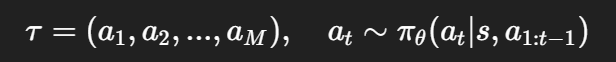
其中策略 πθ根据当前状态 st（以及历史动作）决定下一个动作。

而在 POMO 中：

• 同一个问题实例 sss 下，会从多个起始状态（或节点）同时展开多条轨迹；

• 每条轨迹独立遵循马尔可夫性质；

• 各条轨迹之间互不干扰，只在训练时共享基线（baseline）。

因此，POMO 实际上是在同一个 MDP 环境下进行多次并行采样，每条轨迹都是一个独立的马尔可夫链，只是初始状态不同。

---

（3）数学视角：多起点马尔可夫过程

POMO 将原始的单起点马尔可夫决策过程扩展为：

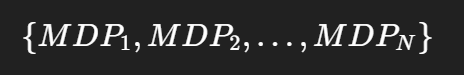
其中每个 MDPi拥有相同的状态转移概率 P、奖励函数 R，但起始状态不同。

这种设计带来的好处：

• 多样化探索，避免策略陷入某一局部最优；

• 利用多个对称起点的轨迹估计共享期望回报 E[R(τi)]，减小方差；

• 更稳定地逼近最优策略 π∗。

---

（4）POMO 中的状态与动作定义举例

以旅行商问题（TSP）为例：

• 状态（State）：当前访问的节点序列、剩余未访问节点；

• 动作（Action）：选择下一个访问的节点；

• 转移（Transition）：将所选节点加入路径；

• 奖励（Reward）：负的路径总长度（目标为最小化距离）。

每个起点形成一条独立的马尔可夫路径（trajectory），整个并行过程是多个 MDP 实例的集合。

🧩 七、POMO 的后处理机制（Post-processing in POMO）

（1）后处理的动机

虽然 POMO 在强化学习框架下已经能直接生成高质量的解，但组合优化问题的复杂性决定了：

• 模型输出的解往往是近似最优；

• 通过一些后处理步骤（post-processing），可进一步优化结果质量。

POMO 的后处理思想来源于传统启发式算法（如 LKH、2-opt），但它在实现上更轻量、更高效，特别是结合了“实例增强”和“多贪心推理”的思路。

---

（2）主要的后处理方法

POMO 的后处理主要包括以下三种类型：

① 多贪心推理（Multiple Greedy Rollouts）

• 传统 Attention Model（AM）或 REINFORCE 在推理时，只生成一条贪心路径；

• POMO 从多个起点（N 个起点）生成 N 条贪心路径；

• 然后从这些路径中选择最优的一个作为最终解。

这种方法本质上是一种多候选解后筛选机制（multi-rollout selection），它能有效避免因起点偏置导致的局部最优。

✅ 效果：在推理阶段不增加训练成本的前提下，性能显著提升，TSP100 的最优性差距从 1.07% 降至 0.14%。

---

② 实例增强（Instance Augmentation）

• POMO 借鉴计算机视觉的“测试时增强（Test-time augmentation, TTA）”概念；

• 对原始问题实例做对称变换（翻转、旋转、坐标交换等），生成多个等价问题；

• 对每个增强实例分别推理，然后选择最优解作为最终输出。

例如在 TSP 中：

• 将节点坐标进行镜像变换 (x, y) → (1-x, y)；

• 旋转 (x, y) → (y, x)；

• 或对输入顺序重新排序（input reordering）；

• 这些变化不会改变问题的最优路径，但能引导网络探索不同的策略。

✅ 效果：相当于在后处理阶段进行“数据增强”，提高解的多样性与鲁棒性。

🧮八、 POMO 论文中的公式逐条解析

✅ 总结：POMO 中公式的整体逻辑关系

公式编号	含义	所属阶段	关键作用
(1)	策略生成	训练 & 推理	定义策略网络如何生成动作
(2)	多起点轨迹定义	训练	并行生成 N 条轨迹
(3)	策略梯度	训练	计算参数更新方向
(4)	共享基线	训练	降低方差、稳定训练
(5)	多轨迹最优选择	推理	后处理选出最优解
(6)	期望回报定义	理论目标	强化学习优化目标