无刷直流电机（BLDC）数学模型深度解析

无刷直流电机（BLDC）数学模型深度解析

1. 引言

无刷直流电机（Brushless DC Motor，简称BLDC）作为现代电力电子技术与电机技术相结合的产物，已成为工业自动化、航空航天、电动汽车等领域的核心动力元件。与传统有刷直流电机相比，BLDC电机取消了机械换向器和电刷结构，采用电子换向方式，大大提高了电机的可靠性、效率和使用寿命。

要深入理解BLDC电机的工作原理并设计高性能的控制系统，建立准确的数学模型是至关重要的基础。本文将从电磁原理出发，系统推导BLDC电机的数学模型，为电机控制算法的设计与仿真分析提供理论支撑。

2. BLDC电机基本结构和工作原理

2.1 基本结构组成

BLDC电机主要由以下部分组成：

• 定子：通常采用三相集中式或分布式绕组，绕组按120°电角度对称分布

• 转子：采用永磁体结构，磁极对数通常为2对、4对或更多

• 位置传感器：霍尔传感器、光电编码器或旋转变压器等，用于检测转子位置

2.2 电子换向原理

BLDC电机通过检测转子位置信号，控制逆变器中功率开关器件的导通与关断，实现电子换向。三相六状态控制是BLDC最常用的控制方式，每个60°电角度区间内只有两相导通，另一相悬空，形成六步换相序列。

3. BLDC电机数学模型推导

3.1 基本假设

在建立数学模型前，我们作如下合理假设：

1. 电机三相绕组完全对称，空间互差120°电角度

2. 磁路不饱和，忽略磁滞和涡流效应

3. 永磁体产生的气隙磁场呈梯形波分布

4. 转子的阻尼效应可以忽略

3.2 电压方程

根据基尔霍夫电压定律，三相绕组的电压平衡方程可表示为：

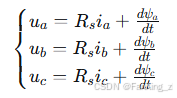
其中，、、为三相相电压，、、为三相相电流，为每相绕组电阻，、、为三相磁链。

各相磁链由电流自感、互感以及永磁体磁链共同作用产生：

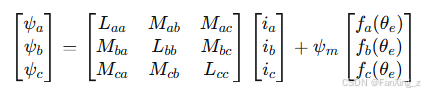
式中，、、为各相自感，、、为相同互感，为永磁体磁链幅值，、、为转子位置相关的梯形波函数，为电角度。

3.3 电感分析

对于表面贴装式BLDC电机，由于气隙均匀，自感和互感可近似为常数：

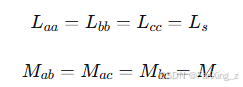
考虑到三相绕组为星形连接且无中线，满足，可得：

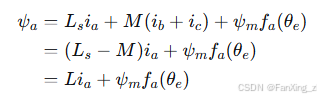
其中，为等效电感。

同理可得其他两相的磁链表达式。将磁链表达式代入电压方程，得到：

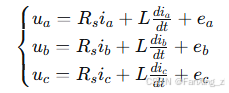
式中，、、为三相反电动势：

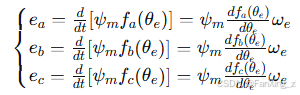
其中，为电角速度。

3.4 反电动势分析

BLDC电机的反电动势波形由永磁体磁场分布和绕组结构决定，理想情况下为梯形波，平顶宽度为120°电角度。梯形波函数可表示为：

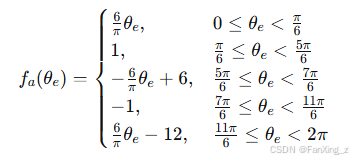
和函数形式相同，相位依次滞后120°。

3.5 转矩方程

根据机电能量转换原理，电磁转矩可表示为：

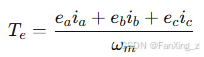
其中，为机械角速度，为极对数。

在任意时刻，只有两相导通，设导通相的反电动势绝对值为，电流绝对值为，则电磁转矩可简化为：

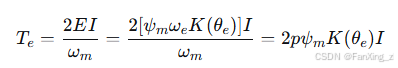
其中，为反电动势波形系数，在平顶区。

3.6 运动方程

根据牛顿第二定律，电机机械运动方程为：

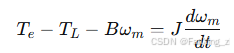
式中，为负载转矩，为粘滞摩擦系数，为转动惯量。

4. 状态空间模型

选取三相电流和机械角速度为状态变量，建立BLDC电机的状态空间模型。

由电压方程可得电流微分方程：

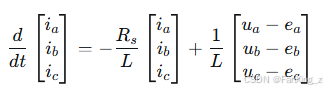
由运动方程可得角速度微分方程：

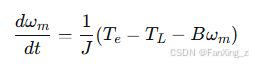
该状态空间模型为非线性系统，可用于系统动态特性分析和控制器设计。

5. dq坐标系下的数学模型

虽然BLDC电机通常不在dq坐标系下分析，但通过适当变换也可得到其dq模型，便于与永磁同步电机对比分析。

定义dq变换矩阵：

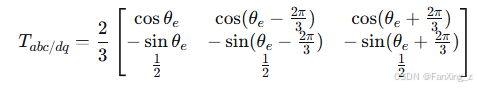
由于BLDC反电动势为非正弦波，dq坐标系下的电压方程包含谐波分量：

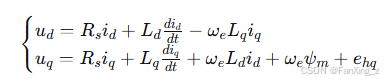
其中，为反电动势谐波在q轴上的分量，电磁转矩为：

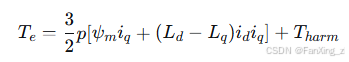
为谐波转矩分量。对于表面贴装式BLDC电机，，转矩公式简化为：

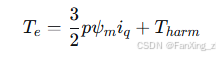
6. 数学模型在控制中的应用

6.1 仿真模型建立

基于上述数学模型，可在Simulink等环境中搭建BLDC电机仿真模型，主要包括以下模块：

• 电压方程模块

• 反电动势计算模块

• 转矩计算模块

• 运动方程模块

• 逆变器模块

• 换相逻辑模块

6.2 控制策略分析

BLDC电机的经典控制策略包括：

• 六步换相控制：基于霍尔位置信号，简单可靠

• 矢量控制：通过坐标变换实现转矩与磁链解耦控制

• 直接转矩控制：通过滞环控制直接调节转矩和磁链

数学模型为这些控制策略的设计与参数整定提供了理论基础。

7. 结论

本文系统推导了BLDC电机的数学模型，从基本的电压方程、磁链方程到转矩方程和运动方程，建立了完整的理论体系。通过对数学模型的分析，可以得出以下结论：

1. BLDC电机的数学模型本质上是非线性、强耦合的多变量系统

2. 反电动势的梯形波特性是BLDC与PMSM的主要区别

3. 状态空间模型为系统动态分析和控制器设计提供了便利

4. dq坐标系下的模型揭示了BLDC与PMSM的内在联系与区别

准确的数学模型是高性能BLDC电机控制系统设计的基础，对于电流环设计、转速估算、位置检测等关键技术具有重要指导意义。随着现代控制理论的发展，基于精确数学模型的先进控制算法将在BLDC电机控制中发挥越来越重要的作用。

参考文献

1. Krishnan, R. (2001). Electric Motor Drives: Modeling, Analysis, and Control. Prentice Hall.

2. Pillay, P., & Krishnan, R. (1989). Modeling, simulation, and analysis of permanent-magnet motor drives. IEEE Transactions on Industry Applications, 25(2), 265-273.

3. 王成元，夏家宽，杨俊友. (2014). 电机现代控制技术. 机械工业出版社.

4. 袁登科，陶生桂. (2010). 交流永磁电机变频调速系统. 机械工业出版社.

---