当前位置：首页 > news >正文

第七届全球校园人工智能算法精英大赛-算法巅峰赛产业命题赛第二赛季--最后一题解读

news 2025/10/20 7:42:48

前言

“全球校园人工智能算法精英大赛”是江苏省人工智能学会举办的面向全球具有正式学籍的全日制高等院校及以上在校学生举办的算法竞赛。其中的算法巅峰赛属于产业命题赛道，这是第二赛季，对最后一道优化题进行浅浅地解读。

在这里插入图片描述

题目描述

给于 n 个机器人，k 个中继器，要求所有n 个机器人都连通的最小代价。
约束规则如下：

机器人存在 R 和 S 两种类型，中继器皆为 C 类型
代价（距离）函数，定义为d=欧式距离的平方，
1. 若两机器人中有一个类型为 S，则其代价函数乘以 0.8*d，否则为 d
2. 机器人和中继器相连，代价函数为 d，
3. 两个中继器不能相连
任意一个机器人都可以直接或间接连通到其他任意机器人
中继器可用可不用
n <= 1500, k <= 1500

求最小连通代价。

这题是属于带约束条件的最小生成树问题，更确切地讲是 Steiner树问题。

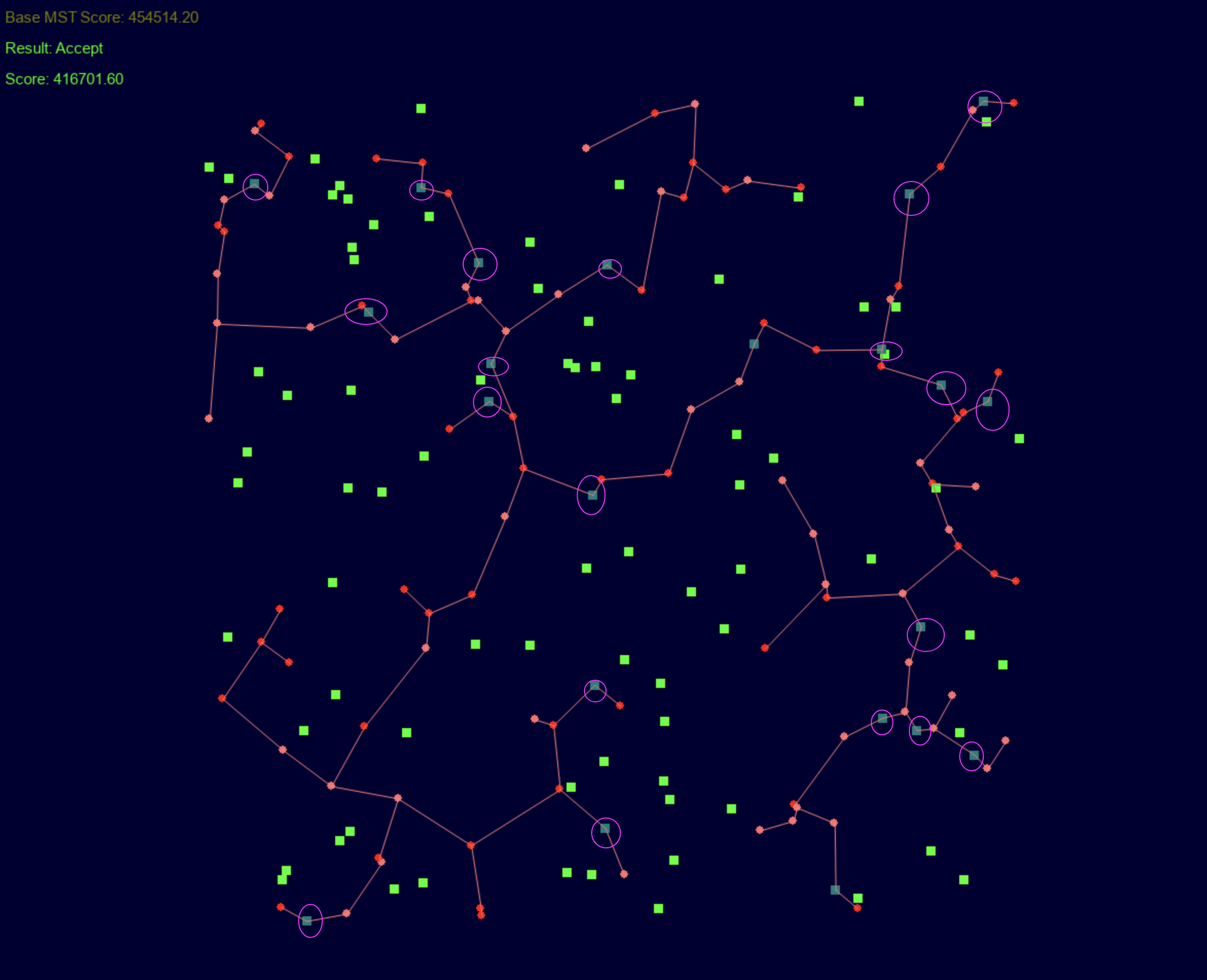
在这里插入图片描述
圆为机器人，方块为中继器，某个 case 的可视化效果图。

思路讲解

再具体讲解之前，先来把玩 2 个机器人和 1 个中继器的关系，三者互联构建一个三角形，以中继器定义的角为视角，其对应的边为 c（两机器人的连边），其他两边为 a，b。
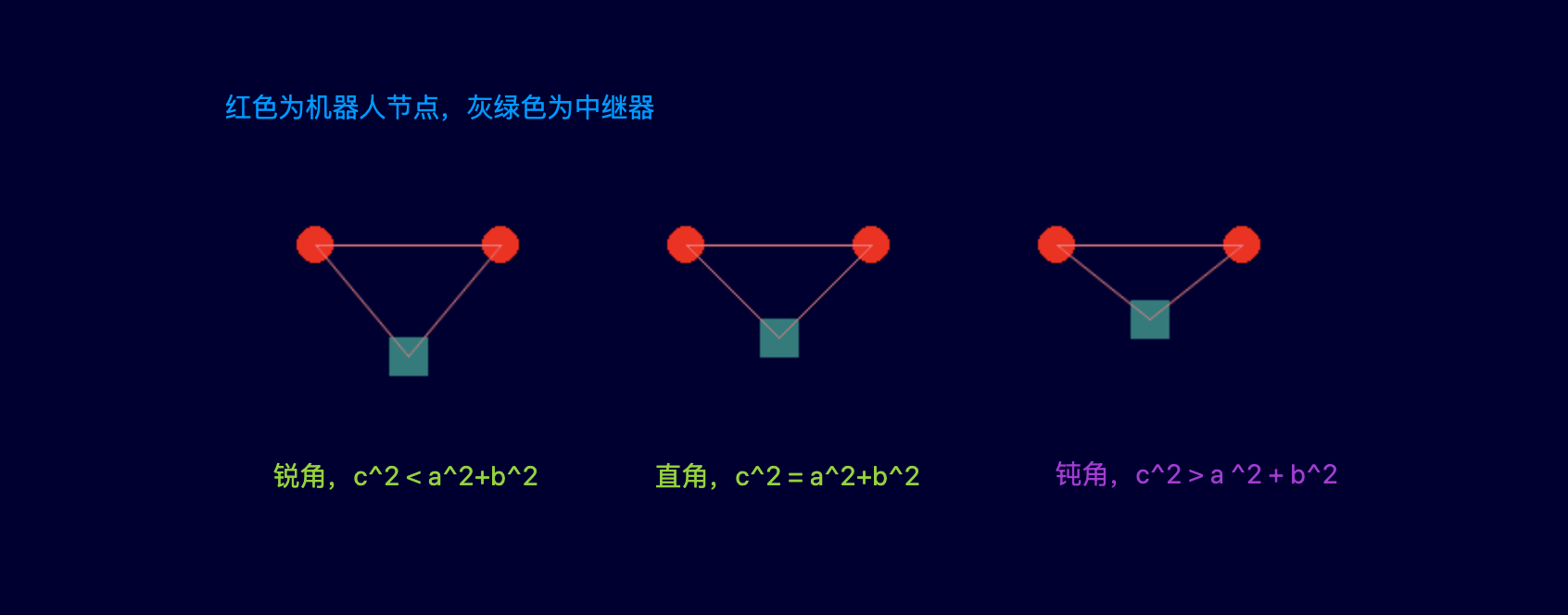
在这里插入图片描述

若为锐角，则满足 ${c^2 < a^2 + b^2}$
若为直角，则满足 ${c^2 = a^2+b^2}$
若为钝角，则满足 ${c^2 > a^2 + b^2}$

从图中，其实可以发现，

当两个机器人的连边和中继器节点构建成一个钝角三角形时，用 a，b 两边替换 c 边，是有收益的（加中继器思路）
当两个机器人的连边和中继器节点构建成一个锐角三角形时，用 c 替代 a，b 也是有收益的（减中继器思路）

而这个观察，是这题优化的核心基石。

后续的所有算法其实都是围绕着这2 点展开。

主流算法

元启发式算法，不断优化中继器节点组合（模拟退火+遗传算法等）
贪心构造
1. 构造一个裸的 MST （不包含中继节点）
2. 添加中继器优化(遍历裸 MST 的每一条边）
3. 再重构 MST
4. 删中继器操作优化（度为 1悬挂，度为 2 的特殊情况）

这 2 个算法，以及后文提到的虚拟边解法，皆属于赛时的顶级算法。

AI 代码解读

这是赛时成绩最好的一份代码

其核心思路是引入 虚拟边

$n^2$ 枚举任意 2 个机器人，如果 2 个机器人其可以加中继器优化，则把该虚拟边（附带中继器节点），代替原先的边，一次操作代价为 $O (k)$ ，整体代价为 $O(n^2 * k)$
然后把机器人之间边按权重进行排序, $O(n^2) * log(n^2)$
使用Kruskal 算法，进行 MST 构造, $O(n^2)$

这边最耗时的问题，瓶颈在第一阶段，但 AI 不愧是 AI，他选择了 K-D 树来实现了最近邻搜索加速。

该思路就是最后的第一，清晰优雅，大道至简

当然该思路也有他的缺陷

构建一个反例， 5 正五边形（5 个顶点是机器人），1 个中心（中继节点）

在这里插入图片描述
该思路输出解为前者(虚拟边无法带入中继器），而最优解为后者

省略中间的计算过程，有兴趣的小伙伴，可以问问 deepseek
在这里插入图片描述
不过该思路在测试数据随机情况下，表现优异，和最优解差距很小（可参阅基准测试）

那这边为啥要讲 AI的解呢？

$目前的 A I 大模型已远超普通人，根本打不过$

基准测试

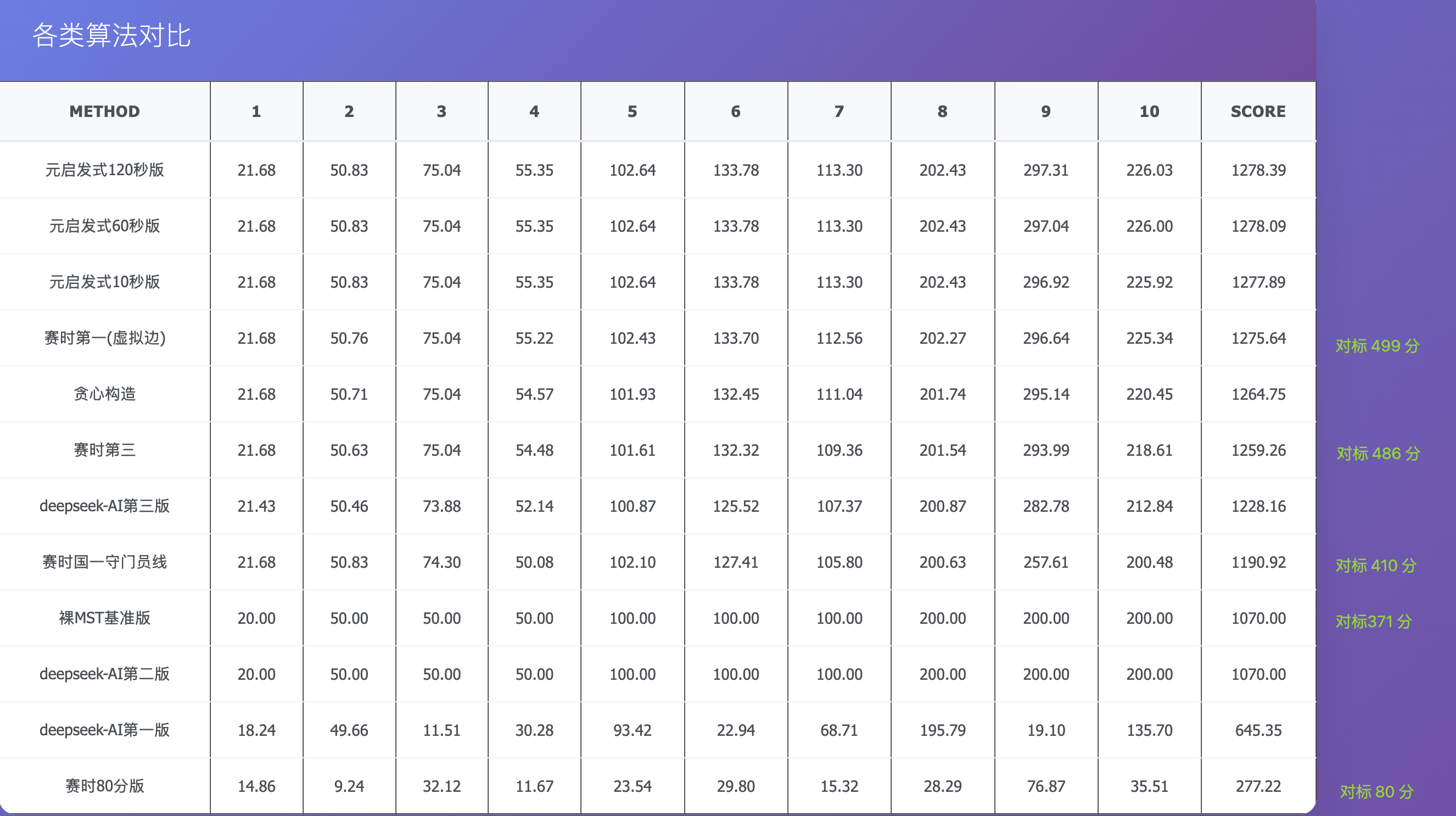
在这里插入图片描述
数据随机生成

case 1，n=10，k=10，权重分 20 
case 2，n=100，k=10，权重分 50
case 3，n=10，k=100，权重分 50
case 4，n=100，k=100，权重分 50
case 5，n=500，k=100，权重分 100
case 6，n=100，k=500，权重分 100
case 7，n=500，k=500，权重分 100
case 8，n=1500，k=100，权重分 200
case 9，n=100，k=1500，权重分 200
case 10，n=1500，k=1500，权重分 200

case 得分为

$权重 * 代价 / 裸 MST 基准代价$

可以观察到