「日拱一码」121 多组学因素分析MOFA
目录
多组学因素分析（Multi-Omics Factor Analysis, MOFA）介绍
什么是多组学因素分析？
MOFA 能解决什么问题？
MOFA 模型的工作原理
MOFA 的结果解读
代码示例
多组学因素分析（Multi-Omics Factor Analysis, MOFA）介绍
什么是多组学因素分析？
多组学因素分析（MOFA）是一种无监督的统计模型，用于整合多个组学数据集（如基因组、转录组、蛋白质组、表观基因组等），并从这些数据中提取一个统一的、低维的视图。你可以把它理解为应用于多组学数据的“主成分分析（PCA）”或“因子分析（FA）”的扩展和增强版。
核心思想：MOFA 假设在所有不同的组学数据层（views）背后，存在一组共同的、潜在的驱动因素（称为因素或潜在变量），这些因素共同解释了数据中观察到的变异。例如，一个潜在因素可能代表一个关键的生物学过程（如细胞周期、炎症反应），它同时影响基因的突变、表达和蛋白质丰度。
MOFA 能解决什么问题？
在生物医学研究中，我们经常对同一组样本（如肿瘤病人）进行多种组学测量。MOFA 的强大之处在于：
- 数据整合：将不同来源、不同尺度、不同噪声水平的数据整合到一个统一的框架中。
- 降维：将数万个分子特征（如基因）浓缩成少数几个具有生物学意义的因素（通常为 10-20 个），极大地简化了数据复杂性。
- 识别变异来源：揭示驱动样本间变异的主要因素。这些因素可以是：
- 生物学因素：细胞类型组成、肿瘤亚型、致病通路激活、患者性别等。
- 技术因素：批次效应、实验误差等。
- 样本聚类：基于共同的潜在因素对样本进行分群，从而发现新的疾病亚型。
- 数据插补：能够预测缺失的组学数据。
MOFA 模型的工作原理
MOFA 模型可以直观地理解为一种矩阵分解技术：
组学数据矩阵≈权重矩阵×因素矩阵
更具体地说，对于每个组学数据层 m：
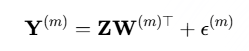
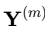：第 m 个组学的数据矩阵（样本 x 特征）。- Z：因素矩阵（样本 x 因素）。这是模型的核心输出，每一列代表一个潜在因素在所有样本中的取值。样本在因素上的得分揭示了其生物学状态。
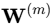：权重矩阵（特征 x 因素）。它表示每个组学的特征（如基因）对每个因素的贡献度。权重大的特征是与该因素最相关的分子。
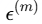：噪声项。
模型通过变分贝叶斯推断来求解 Z 和 ，并能自动确定相关因素的数量。
MOFA 的结果解读
运行 MOFA 后，主要分析以下几个结果：
- 因素数与方差解释：模型会报告每个因素解释了每个组学数据层多少比例的方差。这有助于判断因素的重要性。
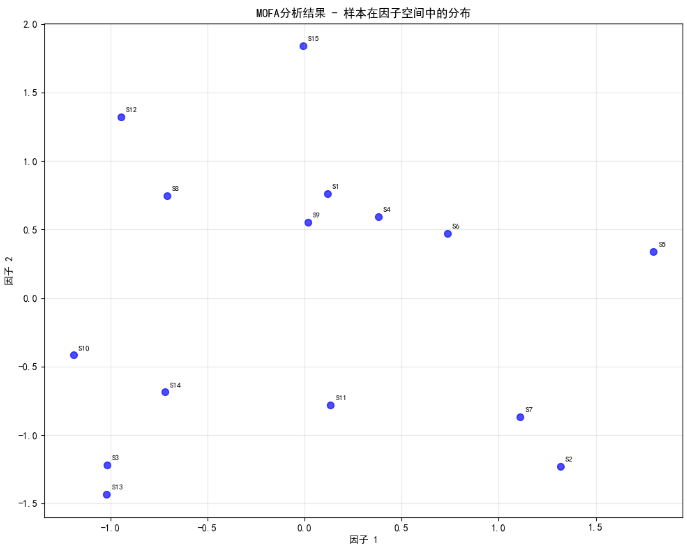
- 因素可视化：绘制样本在因素空间中的分布（如 Factor 1 vs Factor 2 的散点图），观察样本聚类情况。
- 因素与样本元数据关联：将因素得分与样本的临床信息（如肿瘤分期、生存期、治疗反应）进行关联分析，以解释因素的生物学意义。
- 特征权重分析：对于某个重要的因素，找出权重最高的基因/蛋白/代谢物，通过富集分析来揭示其背后的生物学通路。
代码示例
import numpy as np
import matplotlib.pyplot as plt
from mofapy2.run.entry_point import entry_pointprint("开始MOFA分析...")# 1. 设置样本和特征数量
n_samples = 20 # 样本数量
n_features = 15 # 每个视图的特征数量print(f"样本数量: {n_samples}")
print(f"每个视图的特征数量: {n_features}")# 2. 创建数据 - 形状: (特征数, 样本数)
view1_data = np.random.normal(0, 1, (n_features, n_samples))
view2_data = np.random.normal(0, 1, (n_features, n_samples))data = [[view1_data], # 视图1[view2_data] # 视图2
]print(f"数据创建完成，视图数量: {len(data)}")# 3. 初始化MOFA
ent = entry_point()# 4. 设置数据
ent.set_data_matrix(data)# 5. 设置模型参数
ent.set_model_options(factors=2) # 减少因子数量
ent.set_train_options(iter=200, seed=42, verbose=False)# 6. 训练模型
print("训练模型中...")
ent.build()
ent.run()
print("模型训练完成!")# 7. 提取因子
factors = ent.model.nodes["Z"].getExpectation()
print(f"因子矩阵形状: {factors.shape}") # (15, 2)plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.figure(figsize=(10, 8))plt.scatter(factors[:, 0], factors[:, 1], s=50, alpha=0.7, color='blue')plt.xlabel('因子 1')
plt.ylabel('因子 2')
plt.title('MOFA分析结果 - 样本在因子空间中的分布')
plt.grid(True, alpha=0.3)# 添加样本编号
for i in range(factors.shape[0]):plt.annotate(f'S{i+1}', (factors[i, 0], factors[i, 1]),xytext=(5, 5), textcoords='offset points', fontsize=8)plt.tight_layout()
plt.show()