数值计算-线性方程组的迭代解法
线性方程组的迭代解法
1.迭代法基本理论
矩阵的谱半径



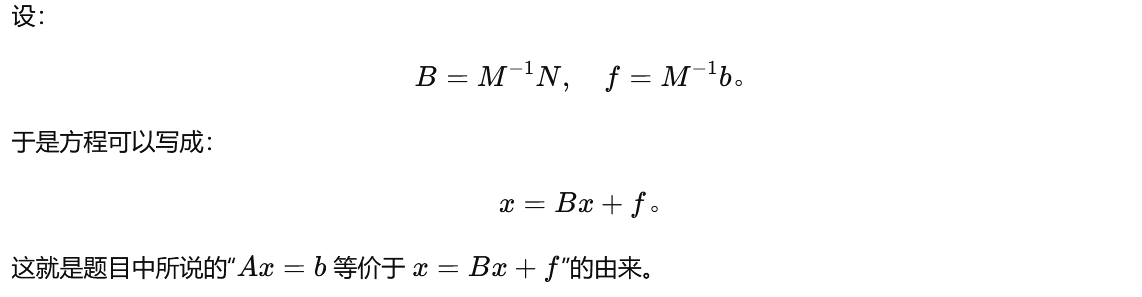
迭代法收敛的条件




矩阵特征向量的性质

2.经典迭代法
2.1 Jacobi迭代法(雅可比)
条件:矩阵A的对角元不为0


2.2 G-S (Gauss-Seidel)迭代法
条件:矩阵A的对角元不为0
有一半填上新的值(左下角)
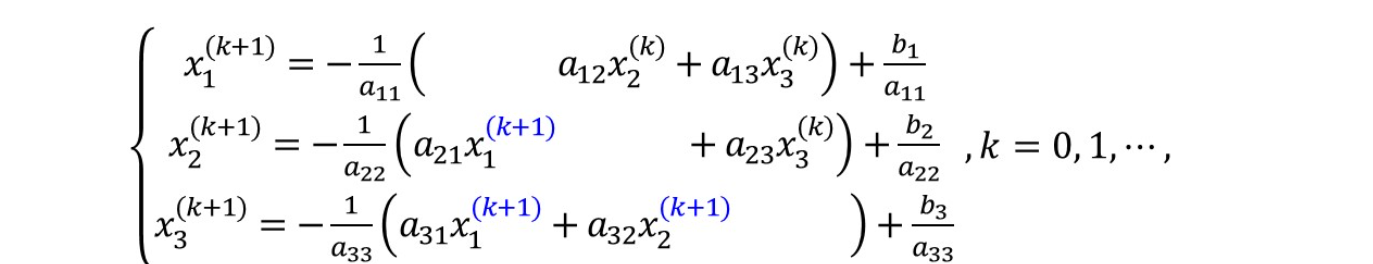


2.3 SOR (Successive Over Relation)迭代法

雅可比迭代法



收敛条件

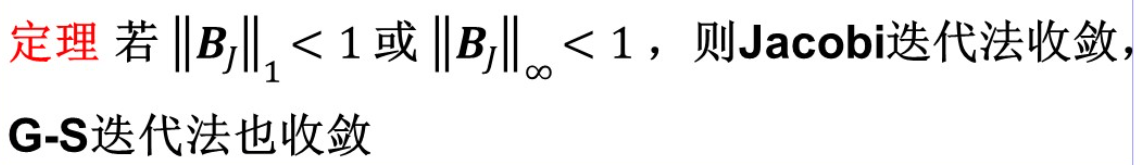
严格对角占优

矩阵的谱半径



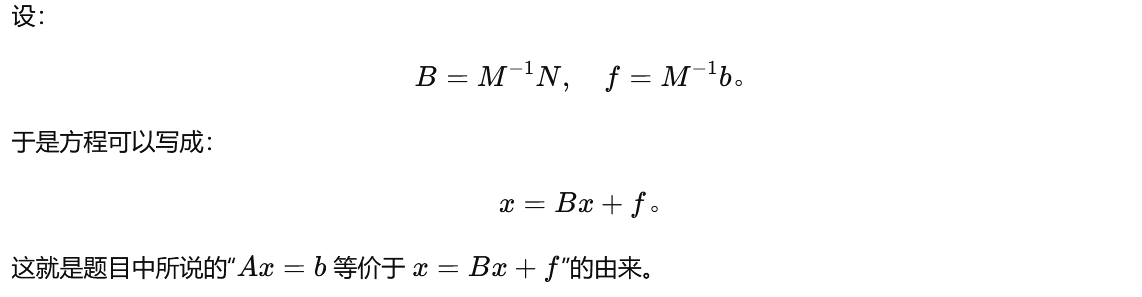
迭代法收敛的条件




矩阵特征向量的性质

条件:矩阵A的对角元不为0


条件:矩阵A的对角元不为0
有一半填上新的值(左下角)
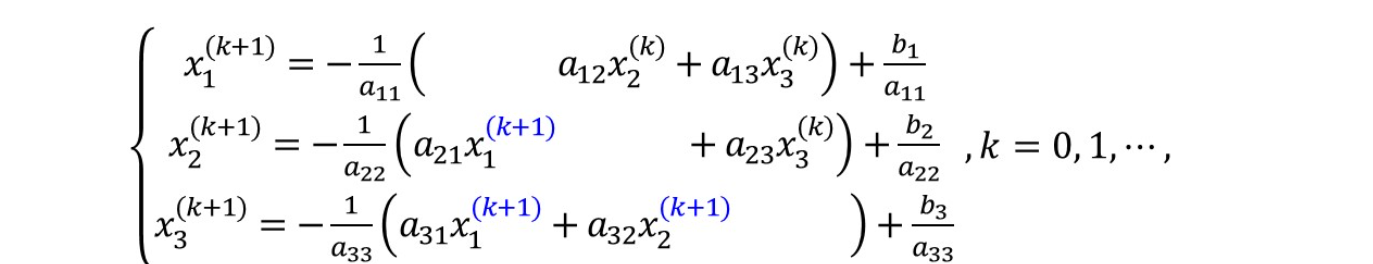



雅可比迭代法



收敛条件

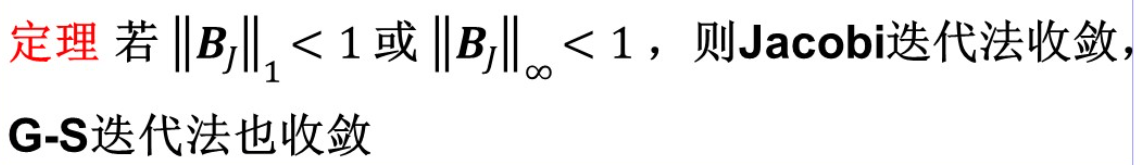
严格对角占优
