当前位置：首页 > news >正文

逻辑回归实战：泰坦尼克号生存预测

news 2025/10/16 7:12:24

一、逻辑回归的基本概念

逻辑回归（Logistic Regression）是一种广泛应用于分类问题的统计学习方法，尽管名称中包含 "回归"，但它实际上是一种分类算法。逻辑回归主要用于解决二分类问题（是 / 否、正 / 负、0/1），通过计算事件发生的概率来进行分类判断。

与线性回归不同，逻辑回归的输出值被限制在 0 到 1 之间，这使得它非常适合处理分类任务。其核心思想是将线性回归的输出通过一个激活函数（通常是 Sigmoid 函数）映射到 [0,1] 区间，从而得到事件发生的概率。

二、逻辑回归的数学原理

1. Sigmoid 函数

Sigmoid 函数是逻辑回归的核心，其数学表达式为：

$\sigma \left ( z \right )= \frac{1}{1+e^{-z}}$

其中z是线性回归的输出，即 $z=w_{0}+w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}$ ， $w$ 为模型参数， $x$ 为输入特征。

Sigmoid 函数具有以下特点：

输出值范围在 (0,1) 之间
当z=0时，输出值为 0.5
当z→+∞时，输出值趋近于 1
当z→−∞时，输出值趋近于 0

2. 决策边界

通过 Sigmoid 函数得到概率值后，我们需要设定一个阈值（通常为 0.5）来进行分类：

当σ(z)≥0.5时，预测为正类（1）
当σ(z)<0.5时，预测为负类（0）

这相当于当z≥0时预测为正类，z<0时预测为负类，z=0即为决策边界。

3. 损失函数

逻辑回归使用交叉熵损失函数（Cross-Entropy Loss）来衡量预测值与真实值之间的差异：

对于二分类问题，损失函数为： $L\left ( y,\hat{y} \right )=-y\log \left ( \hat{y} \right )-\left ( 1-y \right )\log \left ( 1-\hat{y} \right )$

其中y是真实标签（0 或 1）， $\hat{y}$ 是预测的概率值。

模型训练的目标是通过优化算法（如梯度下降）找到使损失函数最小化的参数w。

三、Python 实现逻辑回归的步骤

使用 Python 实现逻辑回归通常包括以下步骤：

数据准备与探索
数据预处理（缺失值处理、特征编码等）
划分训练集和测试集
模型训练
模型评估
结果分析与可视化

四、完整案例：泰坦尼克号生存预测

下面我们将通过泰坦尼克号数据集来演示逻辑回归的具体应用，预测乘客是否能够幸存。

1. 数据准备

首先导入必要的库并加载数据：

# 导入必要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report, roc_curve, auc
from sklearn.impute import SimpleImputer# 从本地文件加载数据（无需网络）
# 请确保titanic.csv文件与该脚本在同一目录下
try:titanic = pd.read_csv('titanic.csv')print("数据加载成功！")
except FileNotFoundError:print("错误：未找到titanic.csv文件，请确保该文件与脚本在同一目录下")print("请从以下地址下载文件：https://raw.githubusercontent.com/mwaskom/seaborn-data/master/titanic.csv")exit()# 查看数据基本信息
print("数据集形状:", titanic.shape)
print("\n前5行数据:")
print(titanic.head())# 查看数据缺失情况
print("\n数据缺失情况:")
print(titanic.isnull().sum())# 数据探索：查看生存情况分布
print("\n生存情况分布:")
print(titanic['survived'].value_counts(normalize=True))# 可视化生存情况与其他特征的关系
plt.figure(figsize=(15, 10))# 性别与生存关系
plt.subplot(2, 2, 1)
sns.countplot(x='sex', hue='survived', data=titanic)
plt.title('Survival by Sex')# 船舱等级与生存关系
plt.subplot(2, 2, 2)
sns.countplot(x='pclass', hue='survived', data=titanic)
plt.title('Survival by Pclass')# 年龄与生存关系
plt.subplot(2, 2, 3)
sns.histplot(data=titanic, x='age', hue='survived', multiple='stack', bins=20)
plt.title('Survival by Age')# 登船港口与生存关系
plt.subplot(2, 2, 4)
sns.countplot(x='embarked', hue='survived', data=titanic)
plt.title('Survival by Embarked')plt.tight_layout()
plt.show()# 选择特征和目标变量
features = ['pclass', 'sex', 'age', 'sibsp', 'parch', 'fare', 'embarked']
X = titanic[features]
y = titanic['survived']# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定义特征预处理管道
# 数值型特征
numeric_features = ['age', 'sibsp', 'parch', 'fare']
numeric_transformer = Pipeline(steps=[('imputer', SimpleImputer(strategy='median')),  # 用中位数填充缺失值('scaler', StandardScaler())  # 标准化
])# 分类型特征
categorical_features = ['pclass', 'sex', 'embarked']
categorical_transformer = Pipeline(steps=[('imputer', SimpleImputer(strategy='most_frequent')),  # 用最频繁值填充缺失值('onehot', OneHotEncoder(handle_unknown='ignore'))  # 独热编码
])# 组合所有预处理步骤
preprocessor = ColumnTransformer(transformers=[('num', numeric_transformer, numeric_features),('cat', categorical_transformer, categorical_features)])# 创建并训练逻辑回归模型管道
model = Pipeline(steps=[('preprocessor', preprocessor),('classifier', LogisticRegression(random_state=42, max_iter=1000))
])model.fit(X_train, y_train)# 在测试集上进行预测
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test)[:, 1]  # 正类的预测概率# 模型评估
print("\n模型评估结果:")
print(f"准确率 (Accuracy): {accuracy_score(y_test, y_pred):.4f}")print("\n混淆矩阵:")
cm = confusion_matrix(y_test, y_pred)
print(cm)# 可视化混淆矩阵
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', cbar=False)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()print("\n分类报告:")
print(classification_report(y_test, y_pred))# ROC曲线和AUC
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)
roc_auc = auc(fpr, tpr)plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()# 提取并可视化特征重要性
# 获取特征名称
categorical_encoder = model.named_steps['preprocessor'].named_transformers_['cat'].named_steps['onehot']
cat_feature_names = list(categorical_encoder.get_feature_names_out(categorical_features))
feature_names = numeric_features + cat_feature_names# 获取特征系数
coefficients = model.named_steps['classifier'].coef_[0]# 创建特征重要性DataFrame
feature_importance = pd.DataFrame({'Feature': feature_names,'Importance': coefficients
})# 按重要性排序
feature_importance = feature_importance.sort_values('Importance', ascending=False)# 可视化特征重要性
plt.figure(figsize=(12, 8))
sns.barplot(x='Importance', y='Feature', data=feature_importance)
plt.title('Feature Importance in Logistic Regression')
plt.show()# 分析特征重要性
print("\n最重要的5个正相关特征:")
print(feature_importance.head(5))
print("\n最重要的5个负相关特征:")
print(feature_importance.tail(5))

泰坦尼克号生存预测逻辑回归实现

数据加载成功！
数据集形状: (891, 15)前5行数据:survived  pclass     sex   age  ...  deck  embark_town  alive  alone
0         0       3    male  22.0  ...   NaN  Southampton     no  False
1         1       1  female  38.0  ...     C    Cherbourg    yes  False
2         1       3  female  26.0  ...   NaN  Southampton    yes   True
3         1       1  female  35.0  ...     C  Southampton    yes  False
4         0       3    male  35.0  ...   NaN  Southampton     no   True[5 rows x 15 columns]数据缺失情况:
survived         0
pclass           0
sex              0
age            177
sibsp            0
parch            0
fare             0
embarked         2
class            0
who              0
adult_male       0
deck           688
embark_town      2
alive            0
alone            0
dtype: int64生存情况分布:
survived
0    0.616162
1    0.383838
Name: proportion, dtype: float64模型评估结果:
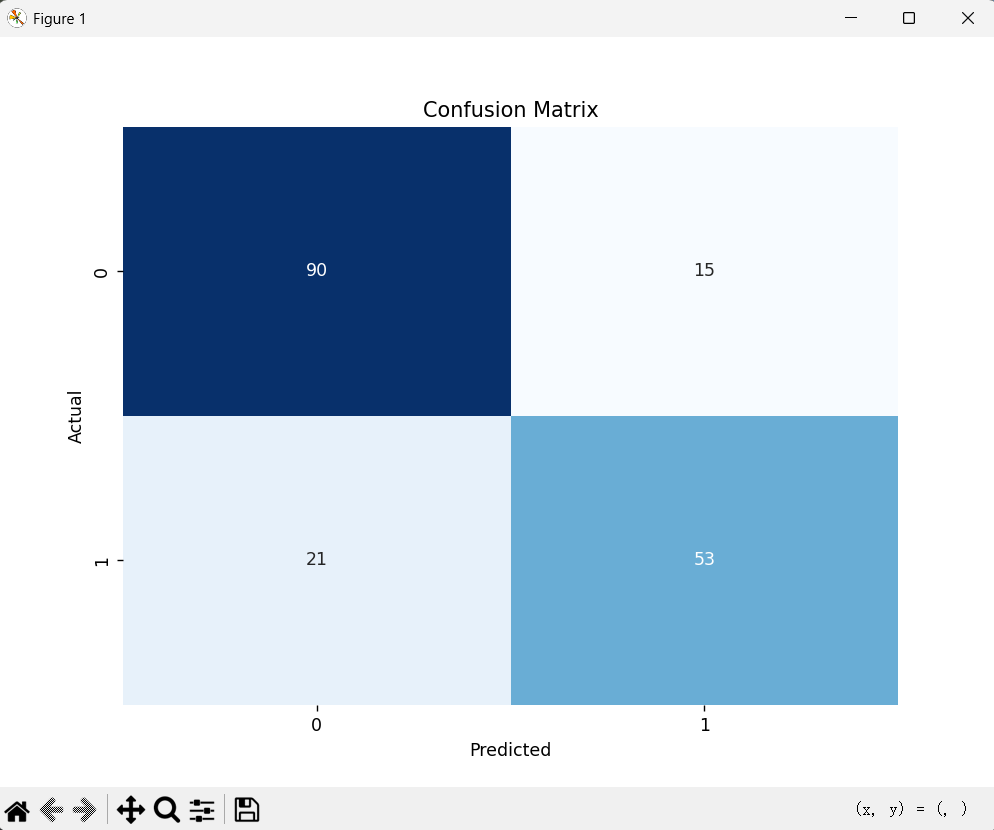
准确率 (Accuracy): 0.7989混淆矩阵:
[[90 15][21 53]]

2. 代码解析

上述代码实现了一个完整的逻辑回归分类流程，主要包括以下几个部分：

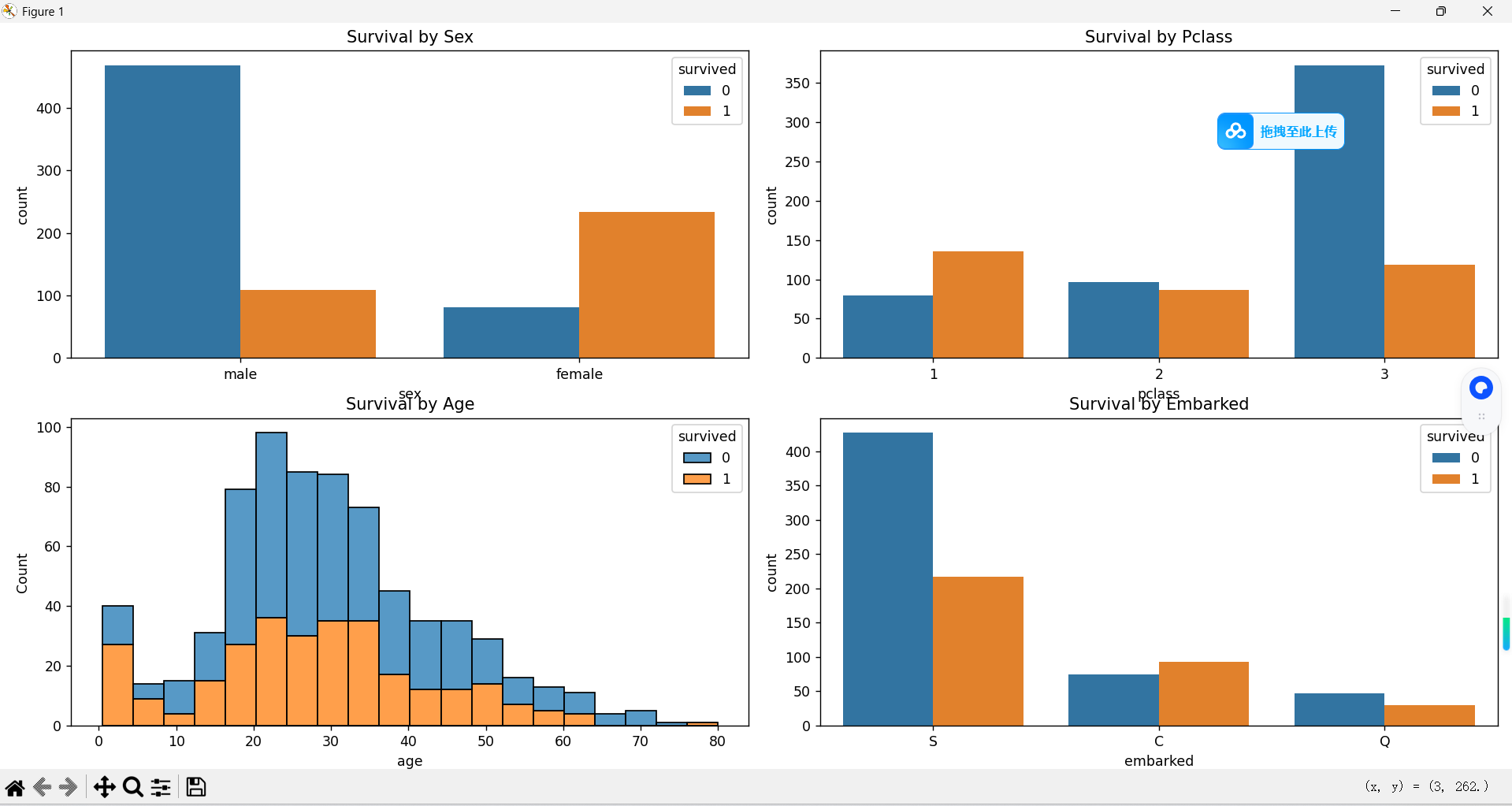
（1）数据探索

首先加载泰坦尼克号数据集并进行初步探索，了解数据的基本情况，包括数据形状、缺失值分布以及生存情况的基本统计。通过可视化分析，我们可以发现一些直观的模式，例如女性生存率高于男性，头等舱乘客生存率高于其他舱位等。

（2）数据预处理

针对不同类型的特征（数值型和分类型），我们设计了不同的预处理管道：

数值型特征：使用中位数填充缺失值，并进行标准化处理
分类型特征：使用最频繁值填充缺失值，并进行独热编码处理

这种预处理方式可以有效处理数据中的缺失值，并将原始数据转换为适合逻辑回归模型输入的格式。

（3）模型训练与评估

我们使用sklearn库中的LogisticRegression类构建模型，并通过管道（Pipeline）将数据预处理和模型训练整合在一起，提高了代码的简洁性和可维护性。

模型评估采用了多种指标：

准确率（Accuracy）：整体预测正确的比例
混淆矩阵：展示真正例（TP）、假正例（FP）、真负例（TN）、假负例（FN）的分布
分类报告：包含精确率（Precision）、召回率（Recall）、F1 分数等详细指标
ROC 曲线和 AUC 值：评估模型的区分能力

（4）特征重要性分析

逻辑回归的一个重要优势是可以解释特征的重要性。通过分析模型的系数，我们可以了解各个特征对预测结果的影响程度和方向（正相关或负相关）。

3. 结果分析

从上述案例的运行结果中，我们可以得出以下结论：

模型性能：通常该模型在泰坦尼克号数据集上可以达到约 80% 左右的准确率，AUC 值在 0.85 左右，说明模型具有较好的分类能力。
特征重要性：
- 性别是最重要的预测因素之一，女性（sex_female）的系数为正，表明女性更有可能幸存
- 船舱等级（pclass）也很重要，头等舱乘客比其他舱位的乘客更有可能幸存
- 年龄也是一个重要因素，年轻乘客的生存率相对较高
模型局限性：虽然逻辑回归在这个数据集上表现不错，但它假设特征与目标变量之间存在线性关系，可能无法捕捉更复杂的非线性模式。