用于汽车雷达应用的步进频率PMCW波形——论文阅读

用于汽车雷达应用的步进频率PMCW波形

M. Kahlert, T. Fei, C. Tebruegge and M. Gardill, “Stepped-Frequency PMCW Waveforms for Automotive Radar Applications,” in IEEE Transactions on Radar Systems, vol. 3, pp. 233-245, 2025, doi: 10.1109/TRS.2025.3528773.

引言：汽车雷达的“分辨率”与“成本”困境

在现代汽车的主动安全和自动驾驶技术中，雷达传感器是实现空间环境感知的重要组成部分，为自适应巡航控制（ACC）、自动紧急制动（AEB）等关键功能提供决策依据。理想情况下，雷达系统需具备厘米级的距离分辨率，这样才能精确区分并排的车辆、行人与背景障碍物等近距离目标。物理学原理决定了雷达的距离分辨率（$\Delta r$）与其发射信号的瞬时带宽（$B$）成反比（$\Delta r=c/2B$）。这意味着，要实现15厘米的分辨率，就需要高达1 GHz的带宽。

传统的主流方案——调频连续波（FMCW）雷达，通过“差拍”技术，在接收端将回波信号与发射信号进行混频，从而将GHz级别的射频带宽信息压缩到MHz级别的基带差拍信号中。这使得FMCW雷达可以使用低成本、低速率的模数转换器（ADC），因而被广泛应用于汽车行业。

然而，近年来学术界和工业界对数字调制方案，如相移键控连续波（PMCW），表现出日益浓厚的兴趣。PMCW雷达具备诸多优势：波形设计极为灵活，能够通过编码区分不同发射天线（CDM），天然适合大规模MIMO阵列；由于脉冲（序列）持续时间短，其最大不模糊速度远高于传统FMCW；不存在FMCW固有的距离-多普勒耦合问题；并且非常适合实现雷达通信一体化（JRC）。但PMCW的致命弱点在于，其基带带宽与射频带宽是等同的。这意味着1 GHz的射频带宽直接要求ADC具备GHz级别的采样能力，这不仅使得ADC器件本身成本剧增，后续的数据存储和处理单元也必须是高速硬件，整体成本呈指数级上升，这对于大规模量产的汽车而言是难以接受的。

为了打破这一僵局，本文提出了一种创新的 步进频率PMCW（SF-PMCW） 雷达波形。其核心策略是“以时间换带宽”：在大幅降低单个脉冲的瞬时带宽（例如，降至100 MHz）以适配低成本ADC的同时，通过在连续发射的脉冲序列之间有规律地、步进式地改变载波频率，从而在整个测量周期（相干处理间隔，CPI）内合成一个等效的宽带宽（例如，1 GHz）。这种方法旨在实现一种理想的平衡：既能获得媲美宽带系统的高距离分辨率，又能得到窄带系统带来的低硬件成本优势。

PMCW雷达系统基础模型

先介绍标准PMCW雷达的信号处理流程。

信号的数学表达

PMCW雷达发射的核心是一个经过二进制相位序列调制的连续波。这个二进制序列由长度为 $N_c$ 的码片构成，每个码片代表一个相位（0或$\pi$）。其等效复基带信号 $X_{BB}(t)$ 可以表达为一个由矩形脉冲构成的序列：

$$X_{BB}(t)=\sum _{n=0}^{N_c-1}x[n_c]\cdot \text{rect}\left(\frac{t-n_c{T}_c}{T_c}\right)$$

其中，$x[n_c]$ 是第 $n_c$ 个码片的值（+1或-1），$T_c$ 是码片持续时间。该基带信号随后被调制到载波频率 $f_c$ 上进行发射，射频信号为：

$$x_{RF}(t)=x_{BB}(t)\exp (j2\pi f_{c}t)$$

当电磁波遇到目标并返回后，接收机收到的信号 $y_{RF}(t)$ 是所有目标回波的叠加，并混杂有噪声。经过前端放大和下变频处理后，得到的基带信号 $y_{BB}(t)$ 为：

$$y_{BB}(t)=\sum _{p=0}^{P-1}{\alpha }_p{x}_{BB}(t-{\tau }_p(t))\exp (-j2\pi f_c{\tau }_p(t))$$

该式中的相位项 $\exp (-j2\pi f_c{\tau }_p(t))$ 包含了目标的距离和速度信息，是后续处理的关键。

距离-速度二维处理

在一个CPI内，雷达连续发射 $N_{seq}$ 个序列。接收到的基带信号被ADC以每个码片一个样本的速率采样，形成一个二维数据矩阵 $Y\in {\mathbb{C}}^{N_c\times N_{seq}}$。这个矩阵的两个维度分别被称为“快时间”（沿矩阵的行，对应单个序列内的采样）和“慢时间”（沿矩阵的列，对应不同序列间的变化）。

1. 距离处理（快时间域）：为了从信号中提取目标的距离信息（即时间延迟 ${\tau }_p$），处理的第一步是对矩阵的每一列（代表一个接收序列）与发射的参考序列 $x$ 进行循环互相关运算。这一过程在数学上等效于一个匹配滤波器，可以将信号能量在时间延迟轴上进行压缩，形成尖锐的峰值。其输出是一个相关矩阵 $R$，其中峰值所在的行索引 $k$ 就对应目标的距离。
   $$r[k,n_{seq}]=\sum _{n_c=0}^{N_c-1}{x}^{\ast }[\text{mod}(n_c-k,N_c)]y[n_c,n_{seq}]$$

2. 速度处理（慢时间域）：经过距离处理后，位于同一距离单元 $k$ 的目标，其能量已经汇集到相关矩阵 $R$ 的第 $k$ 行。由于目标在CPI期间的运动，其回波在慢时间维度上会产生一个线性的相位变化，这个相位的变化率即为多普勒频率。因此，对矩阵 $R$ 的每一行数据（沿着慢时间维度）进行离散傅里叶变换（DFT），就可以得到该距离单元上所有目标的多普勒频谱。将所有距离单元的DFT结果组合起来，就形成了一幅距离-多普勒图（Range-Doppler Map），图中的亮点即为探测到的目标。
   $$s[k,m]=\sum _{n_{slow}=0}^{N_{slow}-1}{r}_{acc}[k,n_{slow}]\exp \left(-j2\pi m\frac{n_{slow}}{N_{slow}}\right)$$

创新的步进频率调制方案

本文的核心思想是在上述模型的基础上，引入载波频率 $f_c$ 的时变特性。

线性递增（Up-Only）SF-PMCW波形与耦合问题

最简单的步进频率方案是让载波频率随时间单调递增。例如，每发射一个或多个序列后，载波频率就增加一个固定的步长 $f_{step}$。
$$f_c^{\uparrow }(n_{seq})=f_0+\lfloor \frac{n_{seq}}{N_{acc}}\rfloor f_{step}$$

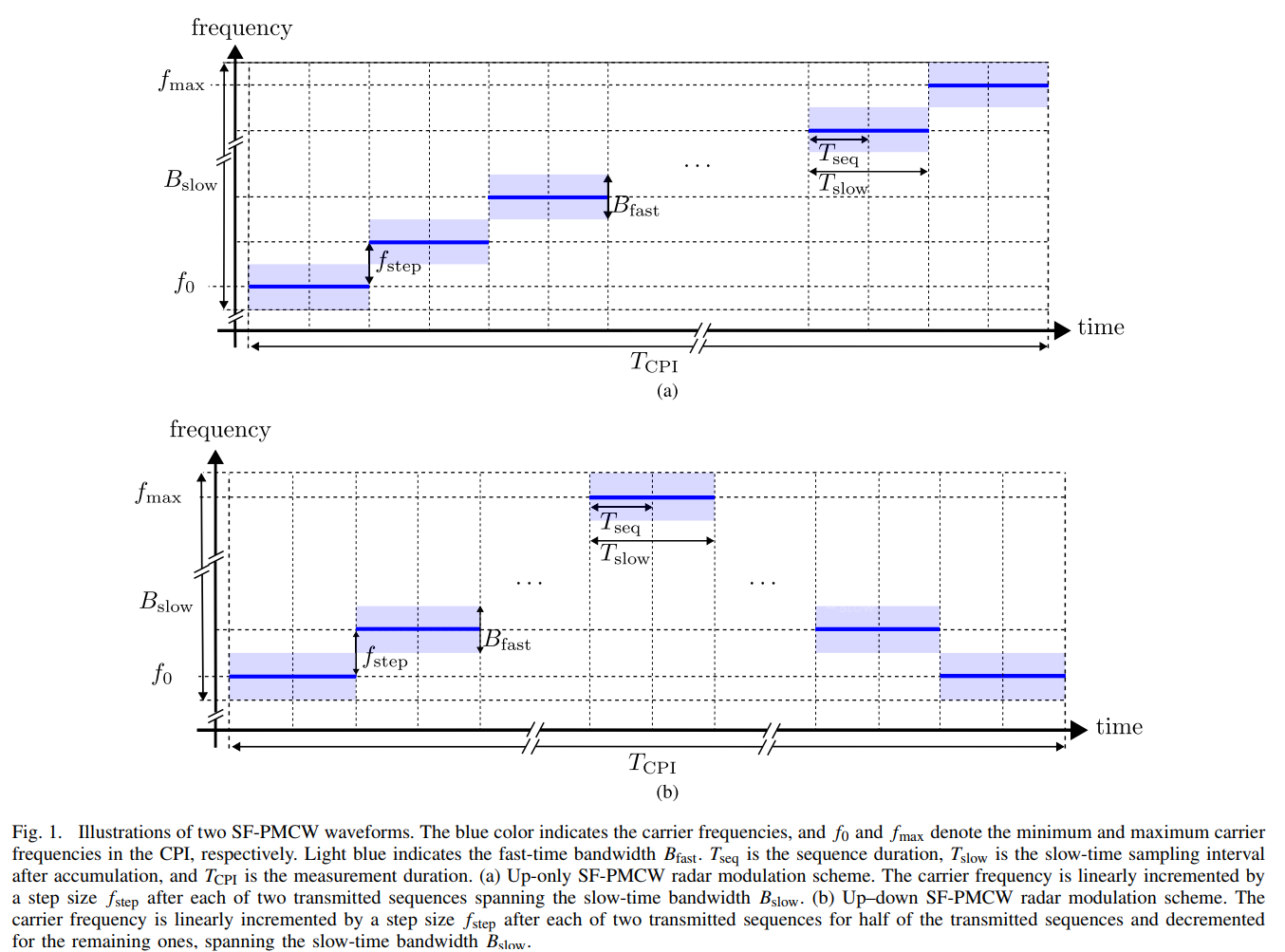
图1(a) 展示了这种“Up-Only”调制方案。图中横轴为时间，纵轴为频率。我们可以看到，载波频率（蓝色粗线）呈阶梯状线性上升。每个阶梯的宽度代表发射若干个序列的时间，高度即为频率步进 $f_{step}$。每个序列自身的瞬时带宽 $B_{fast}$（由浅蓝色区域表示）非常窄，但所有序列覆盖的总频率范围，即合成带宽 $B_{slow}$，则要宽得多。

然而，这种简单的方案却引入了一个副作用：距离-多普勒耦合。在标准PMCW中，载波频率 $f_c$ 恒定，慢时间维度的相位变化仅由速度引起。但在SF-PMCW中，由于 $f_c(n_{seq})$ 自身在变化，导致慢时间相位中额外引入了一个与距离相关的项（详细推导见附录）。最终，测量到的“伪多普勒频率” $f_{\mathcal{D}}$ 变成了真实多普勒频率 $f_D(v_r)$ 和一个由距离 $r_0$ 产生的虚假频率 $f_r(r_0)$ 的线性叠加：
$$f_{\mathcal{D}}(r_0,v_r)=f_r(r_0)+f_D(v_r)=\frac{2B_{slow}{r}_0}{c\cdot T_{CPI}}+\frac{2v_r}{\lambda }$$
这意味着，一个静止的目标（$v_r=0$）也会因为其所在的位置（$r_0$）而在多普勒谱上出现偏移，一个运动的目标其多普勒偏移量也混入了距离信息。要准确估计速度，就必须先知道精确的距离，而精确的距离又需要通过慢时间处理来获得，这就形成了一个无法解开的死循环。这种固有的不确定性使得Up-Only方案在实际应用中几乎不可行。

升降（Up-Down）波形：解耦的精妙之道

为攻克耦合难题，论文提出了一种更为精巧的**“升降（Up-Down）”波形**。其核心是在一个CPI内，将频率步进分为两个阶段：前半段线性升频，后半段线性降频。

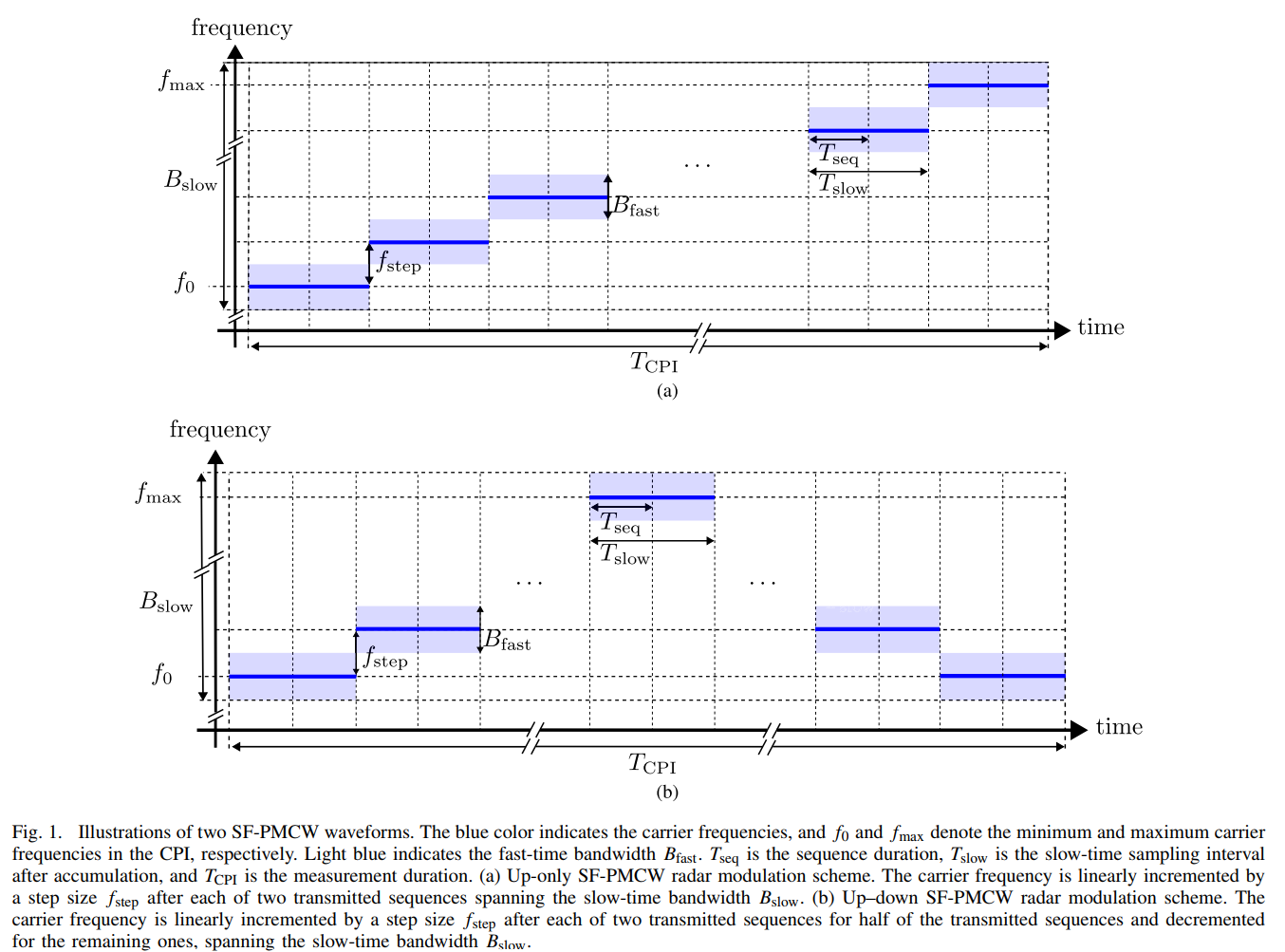
图1(b) 描绘了“Up-Down”调制方案。与图1(a)不同，这里的载波频率（蓝色粗线）在时间轴的中间点发生了转折，形成了一个对称的“V”形或“A”形结构。前半部分频率从 $f_0$ 上升到 $f_{max}$，后半部分则从 $f_{max}$ 下降回 $f_0$。重要的是，整个过程同样扫过了宽阔的合成带宽 $B_{slow}$。

这种对称设计为解耦提供了数学上的解。在信号处理时，需要将升频段和降频段的数据分开，独立进行DFT，从而得到两个不同的多普勒估计结果。对于同一个目标：

• 在升频段，其伪多普勒偏移为：$m_{\uparrow }\propto (+f_r)+f_D$
• 在降频段，由于频率步进的方向相反，距离引入的频率项符号也随之反转：$m_{\downarrow }\propto (-f_r)+f_D$

通过简单的代数运算即可实现解耦：

• 速度估计：将两个多普勒估计值相加（或取平均），距离项 $(+f_r)$ 和 $(-f_r)$ 恰好相互抵消，留下的便是纯净的速度信息：$(m_{\uparrow }+m_{\downarrow })/2\propto f_D$。
• 高精度距离估计：将两个多普勒估计值相减，速度项 $f_D$ 被消除，留下的则是与距离成正比的频率项：$(m_{\uparrow }-m_{\downarrow })/2\propto f_r$。由此可以反算出远比快时间处理精确得多的距离值。

这种Up-Down方案，通过牺牲一半的相干积累时间（导致信噪比理论上损失3dB），解决了距离-多普勒耦合问题，是实现高精度SF-PMCW雷达的关键。

仿真实验与性能验证

论文通过一系列详尽的仿真，系统地评估了所提方案的性能。

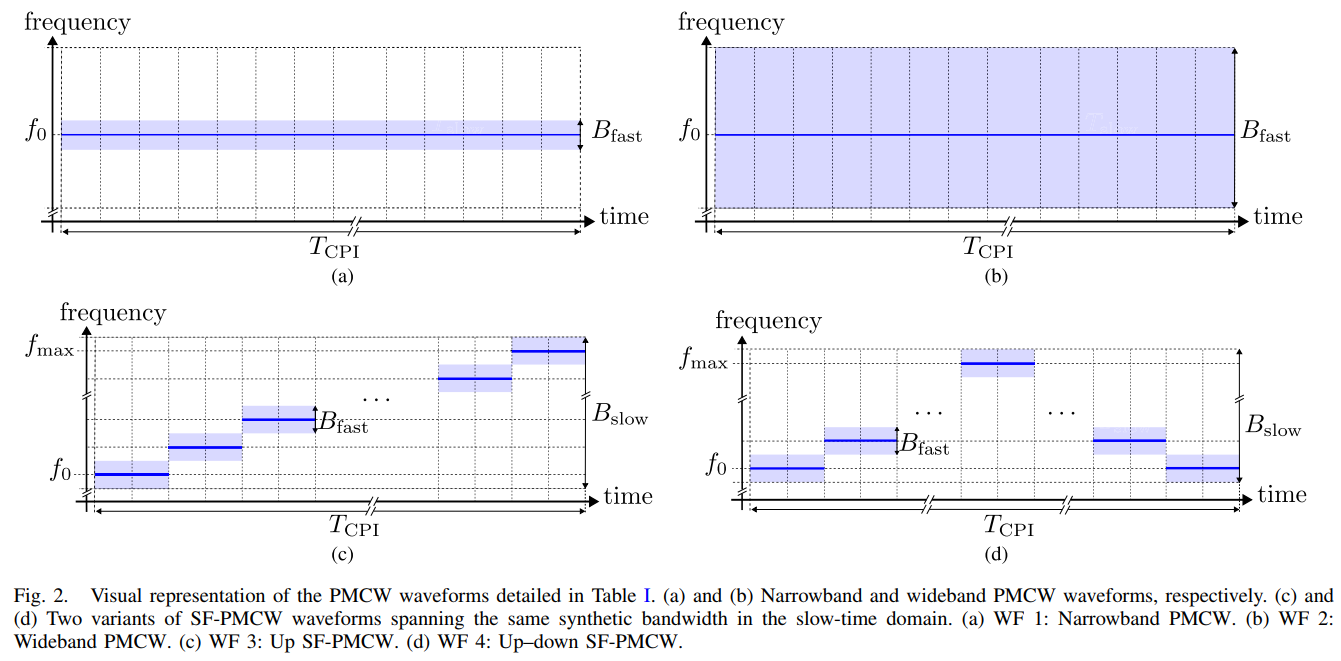
图2 展示了仿真中使用的四种核心波形。(a) WF1是窄带基准（100MHz），(b) WF2是宽带理想性能基准（1000MHz），© WF3是存在耦合问题的Up-Only SF-PMCW，(d) WF4则是本文提出的Up-Down SF-PMCW方案。WF3和WF4的瞬时带宽与WF1相同，但合成带宽与WF2相同。

均方根误差（RMSE）分析

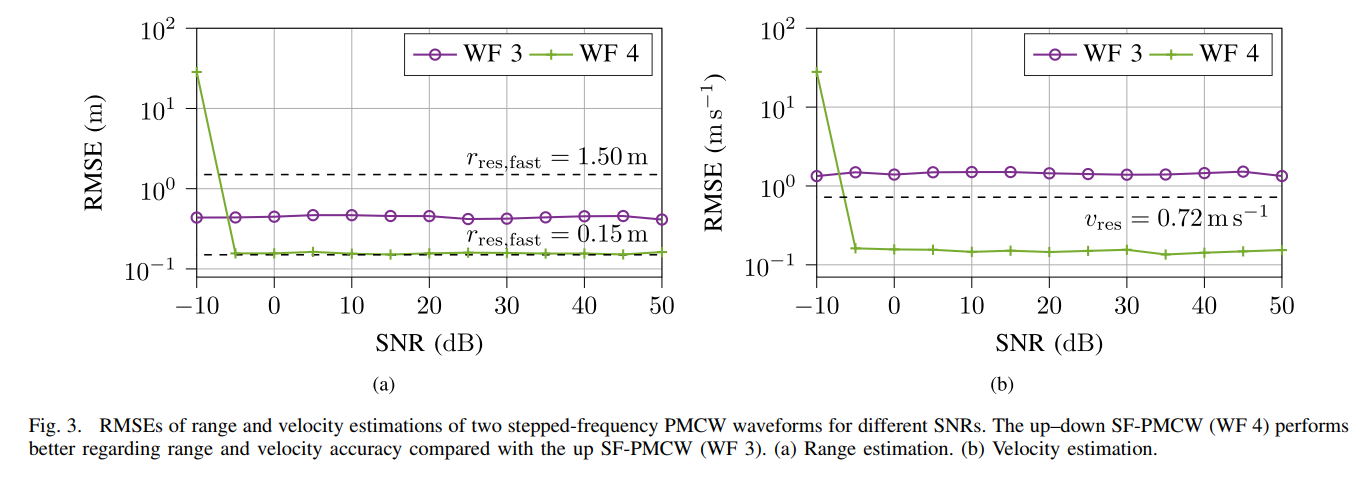
图3 RMSE对比图。图中，横轴为信噪比（SNR），纵轴为估计误差。无论是在(a)距离估计还是(b)速度估计中，代表Up-Down波形（WF4）的曲线都稳定地处于较低的误差水平。相比之下，Up-Only波形（WF3）的误差，尤其是速度误差，高得惊人，验证了理论分析中关于误差传播的判断。

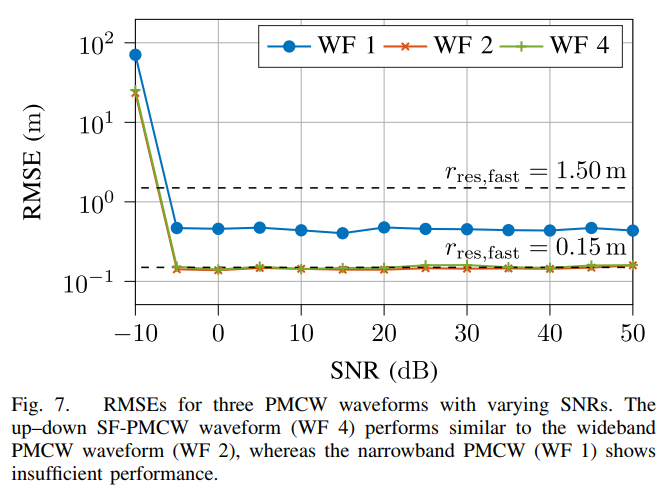
图7 则将WF4与传统方案进行了对比。WF4（星形标记线）的距离估计RMSE曲线与拥有10倍瞬时带宽的WF2（三角形标记线）几乎完全重合，两者都达到了由1000MHz带宽决定的0.15米理论分辨率极限。而与WF4拥有相同瞬时带宽的WF1（圆形标记线），其误差则始终停留在由100MHz带宽决定的1.5米分辨率水平。这一结果证明，SF-PMCW方案用100MHz的硬件成本，实现了1000MHz的系统性能。

目标可分离性验证

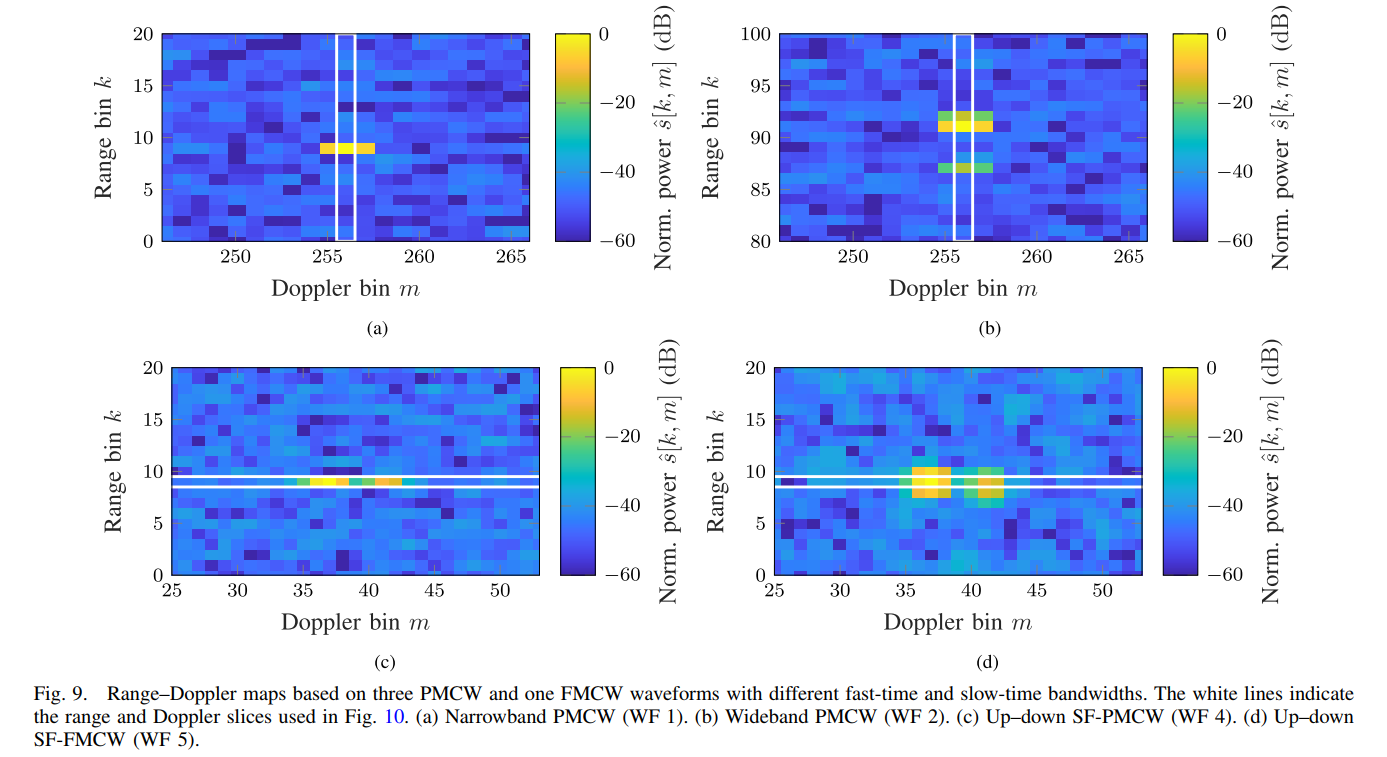
图9的距离-多普勒图展示了SF-PMCW在解决实际问题中的能力。该场景模拟了一个行人站在墙前的棘手情况。

• 在图(a)中，窄带WF1由于分辨率不足，行人和墙的回波在距离上完全重叠，无法区分。
• 在图(b)中，宽带WF2凭借其高距离分辨率，清晰地在两个不同的距离单元（Range bin 91和87）上分开了两个目标。
• 图©展示了WF4。虽然它的快时间分辨率和WF1一样差，但在距离上无法区分目标。然而，由于两个目标处于不同的距离，它们在经过Up-Down处理后，被映射到了不同的（伪）多普勒单元（Doppler bin 41和37）。换言之，WF4利用了（可控的）距离-多普勒耦合效应，将距离上的分离问题转化为了多普勒域上的分离问题，从而成功识别出两个目标。

复杂场景点云生成

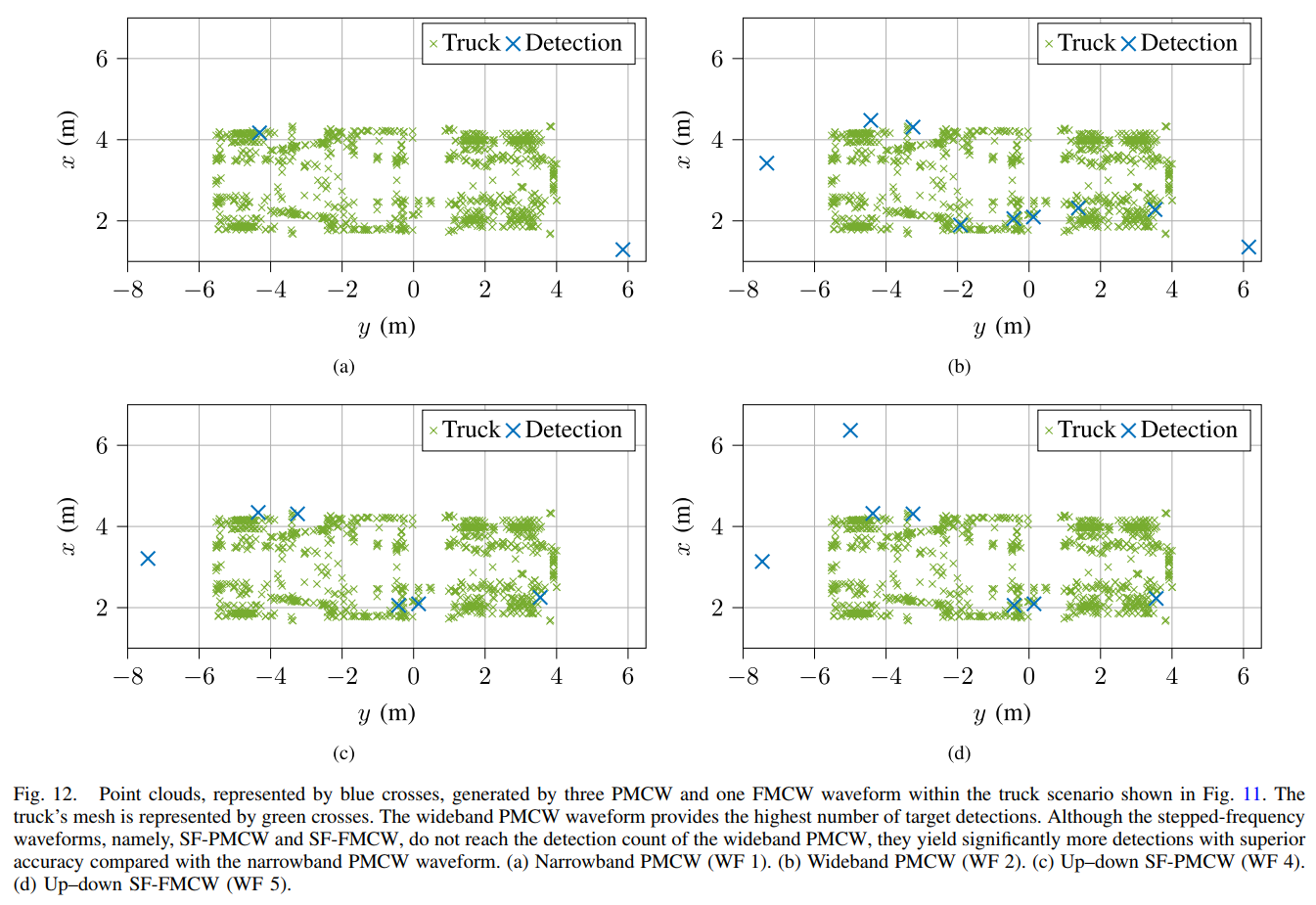
图12展示了在真实的卡车模型场景下，不同波形生成的最终点云。点云的质量直接关系到后续的目标识别、跟踪和场景理解。

• 图(a)的WF1仅能产生零星的几个检测点，无法还原卡车轮廓。
• 图(b)的WF2作为性能标杆，生成了最密集的点云，清晰地勾勒出卡车的侧面和尾部。
• 图©的WF4和图(d)的SF-FMCW（WF5）表现相当出色，虽然点云密度略逊于WF2，但同样生成了足够多的有效检测点来识别卡车的存在和大致轮廓，性能远超WF1。这表明在实际的、复杂的探测任务中，SF-PMCW方案同样具有很强的竞争力。

结论与展望

本研究设计并验证了一种创新的“Up-Down”步进频率PMCW波形。它通过在慢时间维度上合成宽带，并利用对称的升降频结构来解耦距离和速度信息，解决了PMCW雷达在汽车应用中面临的“高分辨率”与“低成本”之间的核心矛盾。

仿真结果证明，一个瞬时带宽仅为100 MHz的SF-PMCW系统，其测距精度、目标分离能力和点云生成质量，均能达到与一个瞬时带宽为1 GHz的传统宽带PMCW系统相媲美的水平。这不仅为PMCW这一先进雷达技术在成本敏感的汽车市场中的大规模商业化应用铺平了道路，同时还完整保留了PMCW在波形灵活性、MIMO应用潜力以及雷达通信一体化方面的固有优势。

---

附录：数学公式推导

1. SF-PMCW中附加相位项的由来

我们从接收基带信号的表达式出发，关注其相位项：$\exp (-j2\pi f_c(n_{seq})\tau (t))$。
在一个CPI中，时间 $t$ 可以表示为慢时间索引 $n_{slow}$ 和快时间 $t^{\prime }$ 的组合，$t=n_{slow}{T}_{slow}+t^{\prime }$，其中 $T_{slow}=N_{acc}{T}_{seq}$。
对于Up-Only波形，$f_c(n_{seq})$ 可以近似为 $f_c(n_{slow})=f_0+n_{slow}{f}_{step}$。
信号的双程延迟 $\tau (t)=\frac{2r(t)}{c}=\frac{2(r_0+v_{r}t)}{c}$。由于在单个 $T_{slow}$ 内目标位移远小于距离，我们可以近似 $\tau (t)\approx \tau (n_{slow})=\frac{2(r_0+v_r{n}_{slow}{T}_{slow})}{c}$。

因此，第 $n_{slow}$ 个慢时间采样点的相位可以写为：
$$\Psi (n_{slow})=-2\pi (f_0+n_{slow}{f}_{step})\left(\frac{2r_0}{c}+\frac{2v_r{n}_{slow}{T}_{slow}}{c}\right)$$
展开后得到：
$$\Psi (n_{slow})=-\frac{4\pi f_0{r}_0}{c}-\frac{4\pi f_0{v}_r}{c}{n}_{slow}{T}_{slow}-\frac{4\pi f_{step}{r}_0}{c}{n}_{slow}-\frac{4\pi f_{step}{v}_r}{c}{n}_{slow}^2{T}_{slow}$$
这个相位表达式包含四项：

1. 常数相位项：不随 $n_{slow}$ 变化。
2. 线性项1（真实多普勒项）：$-\frac{4\pi f_0{v}_r{T}_{slow}}{c}{n}_{slow}=-2\pi \left(\frac{2v_r}{{\lambda }_0}\right)T_{slow}{n}_{slow}$。括号内的项就是真实的多普勒频率 $f_D=\frac{2v_r}{{\lambda }_0}$。这是我们想要测量的项。
3. 线性项2（距离耦合项）：$-\frac{4\pi f_{step}{r}_0}{c}{n}_{slow}$。这是一个由频率步进 $f_{step}$ 和目标距离 $r_0$ 共同引入的、随 $n_{slow}$ 线性变化的附加相位。
4. 二次相位项：这一项会导致多普勒展宽，但在多数汽车场景下影响较小，论文中将其忽略。

在进行DFT时，线性变化的相位会体现为频谱上的一个频移。因此，总的频移由线性项2和线性项3共同决定。

2. 伪多普勒频率的分解

慢时间信号可以模型化为 $s(n_{slow})=A\exp (j\Psi (n_{slow}))$。其瞬时频率 $f_{\mathcal{D}}$ 是相位对时间的导数，在离散时间中，可以看作是相邻采样点间的相位差除以 $2\pi T_{slow}$：
$$f_{\mathcal{D}}=\frac{\Psi (n_{slow})-\Psi (n_{slow}-1)}{-2\pi T_{slow}}$$
只考虑线性项，相位差为：
$$\Delta \Psi =\left(-\frac{4\pi f_0{v}_r{T}_{slow}}{c}\right)-\left(-\frac{4\pi f_{step}{r}_0}{c}\right)$$
因此，伪多普勒频率为：
$$f_{\mathcal{D}}=\frac{1}{-2\pi T_{slow}}\left[\Delta \Psi \right]=\frac{2f_0{v}_r}{c}+\frac{2f_{step}{r}_0}{c{T}_{slow}}$$
注意到 $f_D=\frac{2f_0{v}_r}{c}=\frac{2v_r}{{\lambda }_0}$，以及合成带宽 $B_{slow}=N_{slow}{f}_{step}$ 和 $T_{CPI}=N_{slow}{T}_{slow}$，我们可以将第二项改写为：
$$\frac{2f_{step}{r}_0}{c{T}_{slow}}=\frac{2(B_{slow}/N_{slow})r_0}{c(T_{CPI}/N_{slow})}=\frac{2B_{slow}{r}_0}{c{T}_{CPI}}$$
这个由距离引入的虚假频率就是 $f_r(r_0)$。
最终，我们得到与论文中一致的结论：
$$f_{\mathcal{D}}(r_0,v_r)=f_D(v_r)+f_r(r_0)=\frac{2v_r}{{\lambda }_0}+\frac{2B_{slow}{r}_0}{c{T}_{CPI}}$$
这就从数学上证明了距离-多普勒耦合的来源与形式。对于降频段，频率步进 $f_{step}$ 变为 $-f_{step}$，因此 $f_r(r_0)$ 项的符号也随之变为负，为解耦提供了可能。