当前位置：首页 > news >正文

【数值分析】解线性方程组的迭代法经典算法

news 2025/10/14 9:58:06

1.雅可比迭代法

算法原理

设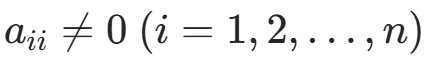，在系数矩阵 A 的分裂 A=D−L−U=M−N 中，选取 M=D，得到解 Ax=b 的雅可比迭代法

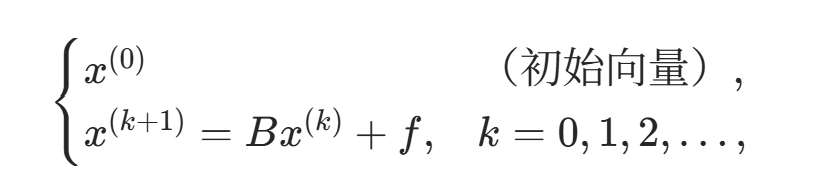
其中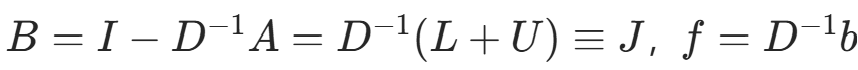。分量公式：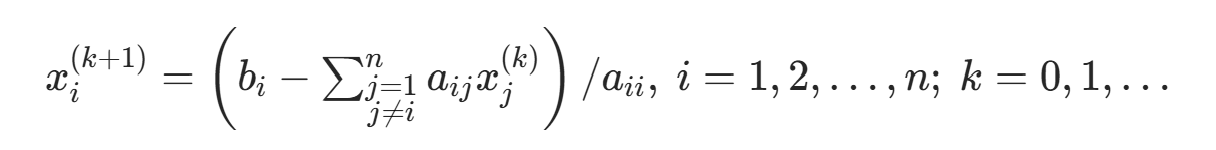

算法步骤：

a. 输入 A,b,ep,it_max；

b. 初始向量 $x_i$ =0 (i=1,…,n)；

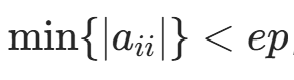c. 若，退出；

d. 对 k=1,…,it_max；

e. 对 i=1,…,n，计算；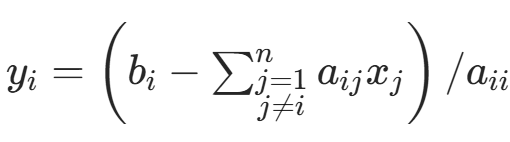

f. 若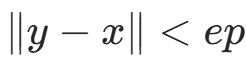，输出 y；否则 x=y，转 e。

MATLAB 程序：

function [x,k] = Jacobi(A,b,ep,it_max)
% A 为系数矩阵，b 为方程组右端，x 为方程组解
% ep 为计算精度，it_max 为最大迭代次数，k 为实际迭代次数
if nargin < 4it_max = 100;
end
if nargin < 3ep = 1e-5;
end
d = diag(A);                % 提取系数矩阵的对角元素
if min(abs(d)) < 1e-10disp('对角矩阵包含零元素'); return;
end
n = length(A);    k = 0;    x = zeros(n,1);    y = zeros(n,1);
while k <= it_maxy = (b - A * x + d .* x) ./ d;if norm(y - x, inf) < epbreak;    endk = k + 1;    x = y;
end

数值实验

例 1：解方程组

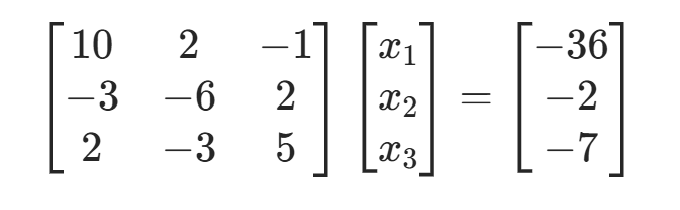
要求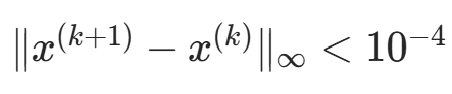时终止。

>> A = [10 2 -1; -3 -6 2; 2 -3 5]; b = [-36 -2 -7]'; ep = 1e-4;
>> [x,k] = Jacobi(A,b,ep)

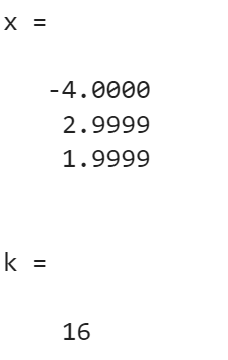
2. 高斯 - 塞德尔迭代法

算法原理：设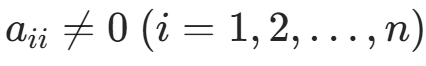，对 A=D−L−U=M−N，取 M=D−L，得迭代法：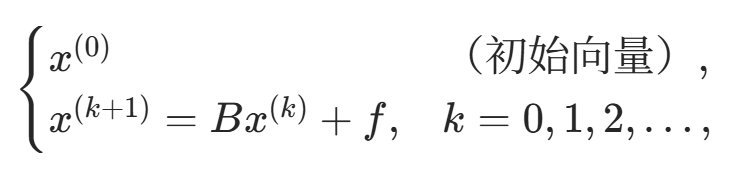

其中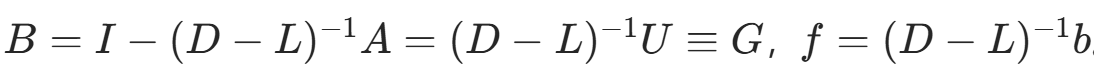

分量公式：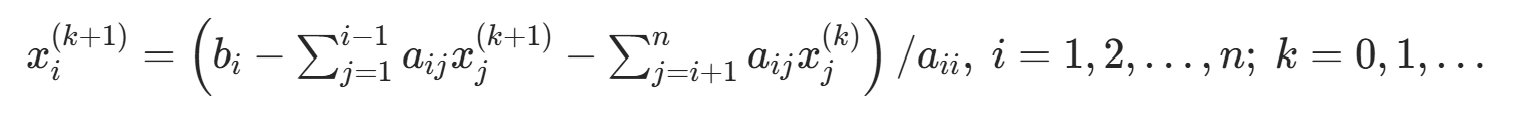

算法步骤：

a. 输入 A,b,ep,it_max；

b. 初始向量 $x_i$ =0 (i=1,…,n)；

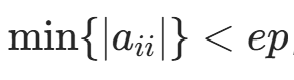c. 若，退出；

d. 对 k=1,…,it_max；

e. 对 i=1,…,n，计算；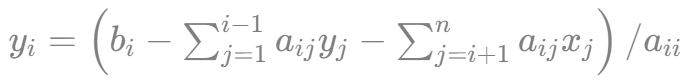

f. 若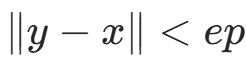，输出 y；否则 x=y，转 e。

与雅可比类似，步骤 e 中 $y_i$ 计算利用了已更新的 $y_j$ (j<i)。

MATLAB 程序：

function [x,k] = Gau_Seid(A,b,ep,it_max)
% A 为系数矩阵，b 为方程组右端，x 为方程组解
% ep 为计算精度，it_max 为最大迭代次数，k 为实际迭代次数
if nargin < 4it_max = 100;
end
if nargin < 3ep = 1e-5;
end
d = diag(A);                % 提取系数矩阵的对角元素
if min(abs(d)) < 1e-10disp('对角矩阵中包含零元素'); return;
end
n = length(A);    k = 0;    x = zeros(n,1);    y = zeros(n,1);
while k <= it_maxy(1) = (b(1) - A(1,2:n) * x(2:n)) / A(1,1);for i = 2:n-1y(i) = (b(i) - A(i,1:i-1) * y(1:i-1) - A(i,i+1:n) * x(i+1:n)) / A(i,i);endy(n) = (b(n) - A(n,1:n-1) * y(1:n-1)) / A(n,n);if norm(y - x, inf) < epbreak;    endk = k + 1;    x = y;
end

数值实验

例 2：解同例 1 的方程组（精度 $10^{-4}$ ）。

>> A = [10 2 -1; -3 -6 2; 2 -3 5]; b = [-36 -2 -7]'; ep = 1e-4;
>> [x,k] = Gau_Seid(A,b,ep)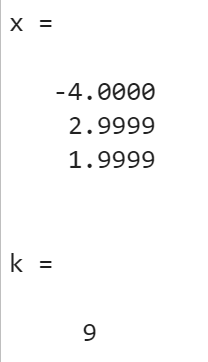

3. 逐次超松弛（SOR）迭代法

算法原理：取分裂矩阵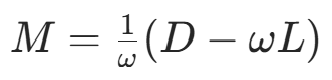（ω>0 为松弛因子），迭代矩阵：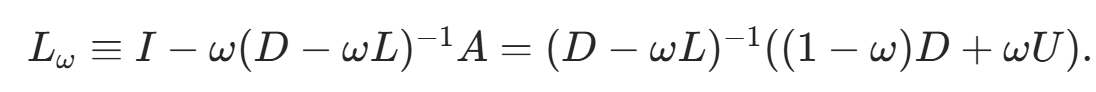

分量公式（ω 为松弛因子）：

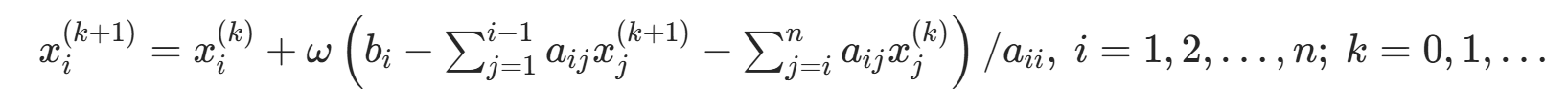
算法步骤：

a. 输入 A,b,ep,it_max；

b. 初始向量 $x_i$ =0 (i=1,…,n)；

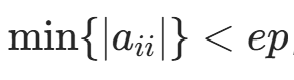c. 若，退出；

d. 对 k=1,…,it_max；

e. 对 i=1,…,n，计算；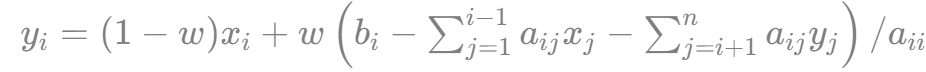

f. 若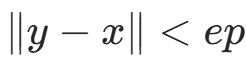，输出 y；否则 x=y，转 e。

MATLAB 程序：

function [x,k] = SOR(A,b,w,ep,it_max)
% A 为系数矩阵，b 为方程组右端，x 为方程组解
% ep 为计算精度，it_max 为最大迭代次数，k 为实际迭代次数，w 为松弛因子
if nargin < 5it_max = 100;
end
if nargin < 4ep = 1e-5;
end
d = diag(A);                % 提取系数矩阵的对角元素
if min(abs(d)) < 1e-10disp('对角矩阵中包含零元素'); return;
end
n = length(A);    k = 0;    x = zeros(n,1);    y = zeros(n,1);
while k <= it_maxy(1) = (1 - w) * x(1) + w * (b(1) - A(1,2:n) * x(2:n)) / A(1,1);for i = 2:n-1y(i) = (1 - w) * x(i) + w * (b(i) - A(i,1:i-1) * y(1:i-1) - A(i,i+1:n) * x(i+1:n)) / A(i,i);endy(n) = (1 - w) * x(n) + w * (b(n) - A(n,1:n-1) * y(1:n-1)) / A(n,n);if norm(y - x, inf) < epbreak;    endk = k + 1;    x = y;
end

数值实验

例 3：解同例 1 的方程组，取 ep= $10^{-4}$ ,it_max=200，松弛因子 ω=0.8,0.9,1.0,1.1,1.2,1.3。

>> A = [10 2 -1; -3 -6 2; 2 -3 5];    b = [-36 -2 -7]';    ep = 1e-4;
>> it_max = 200;    w = 0.8:0.1:1.3;
>> for i = 1:length(w)
>>     [x,k] = SOR(A,b,w(i),ep,it_max)
>> end

x =-4.00002.99991.9999k =15x =-4.00002.99991.9999k =12x =-4.00002.99991.9999k =9x =-4.00003.00002.0000k =7x =-4.00003.00002.0000k =10x =-3.99993.00002.0000k =14

结论：ω=1.1 迭代次数最少，ω=1 为高斯 - 塞德尔迭代。

例 4：讨论迭代法对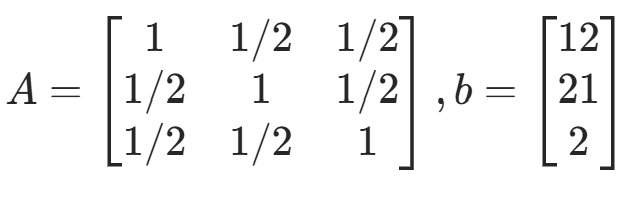

的收敛性。

理论：A 正定，故高斯 - 塞德尔收敛；2D−A 非正定，雅可比不一定收敛；0<ω<2 时 SOR 收敛。
计算（雅可比迭代，结果循环不收敛）：

>> A = [1, 0.5, 0.5; 0.5, 1, 0.5; 0.5, 0.5, 1];    b = [12,21,2]';
>> ep = 1e-5;    it_max = 20:22;    m = length(it_max);
>> for i = 1:m
>> [x,k] = Jacobi(A,b,ep,it_max(i)), z = A * x
>> end

x =12.333330.3333-7.6667k =21z =23.666732.666713.6667x =0.666718.6667-19.3333k =22z =0.33339.3333-9.6667x =12.333330.3333-7.6667k =23z =23.666732.666713.6667

>> ep = 1e-5;    it_max = 100;
>> [x,k] = Gau_Seid(A,b,ep,it_max)

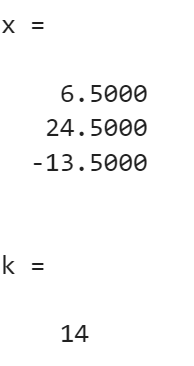
>> w = 0.9:0.05:1.2;    m = length(w);
>> for i = 1:m
>> [x,k] = SOR(A,b,w(i),ep,it_max)
>> end

x =6.500024.5000-13.5000k =17x =6.500024.5000-13.5000k =16x =6.500024.5000-13.5000k =14x =6.500024.5000-13.5000k =14x =6.500024.5000-13.5000k =14x =6.500024.5000-13.5000k =14x =6.500024.5000-13.5000k =15

结论：最佳松弛因子在 ω=1 附近；雅可比不收敛，高斯 - 塞德尔与 SOR 收敛。

4. 共轭梯度法

算法原理：取初始搜索方向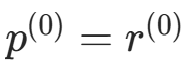，通过 A- 共轭方向迭代，公式：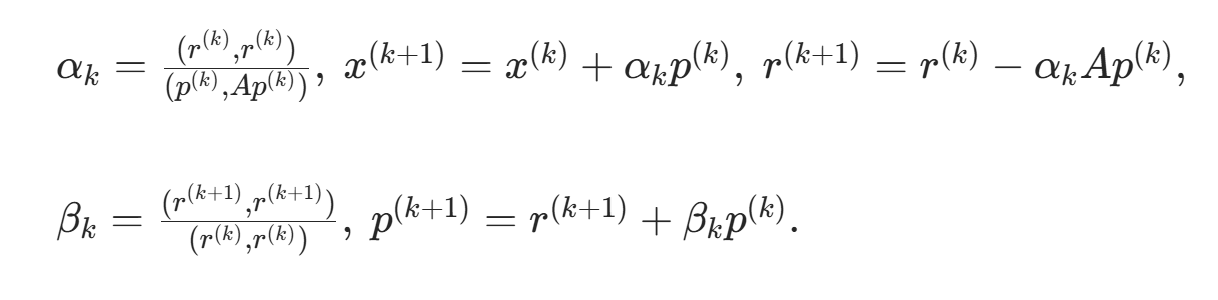

算法步骤：

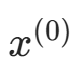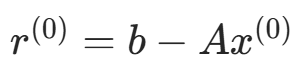(1) 任取，计算，取。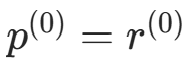

(2) 对 k=1,2,…,n，按上述公式迭代。

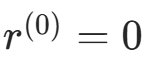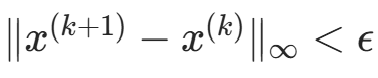(3) 若或，停止。

MATLAB 程序：

function [x,k] = CG(A,b,ep)
[m,n] = size(A);
if m ~= ndisp('系数矩阵非方阵');    return;
elseif m ~= length(b)disp('系数矩阵和右端向量维数不匹配');    return;
end
if A - A' ~= 0disp('系数矩阵非对称');    return;
end
x = zeros(n,1);    r0 = b - A * x;    r0n2 = r0' * r0;    p0 = r0;
for k = 1:nAp = A * p0;    alf = r0n2 / (p0' * Ap);    x1 = x + alf * p0;    r1 = r0 - alf * Ap;if norm(r1, inf) < epx = x1;    return;endif norm(x1 - x, inf) < epx = x1;    return;endr1n2 = r1' * r1;    beta = r1n2 / r0n2;    p1 = r1 + beta * p0;x = x1;    r0 = r1;    p0 = p1;    r0n2 = r1n2;
end

数值实验

例 5：解方程组

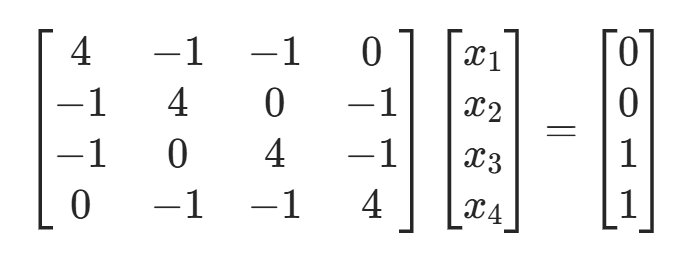
要求。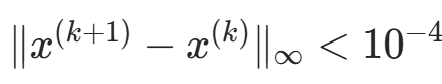

>> A = [4,-1,-1,0; -1,4,0,-1; -1,0,4,-1; 0,-1,-1,4];    b = [0,0,1,1]';    ep = 1e-4;
>> [x,k] = CG(A,b,ep)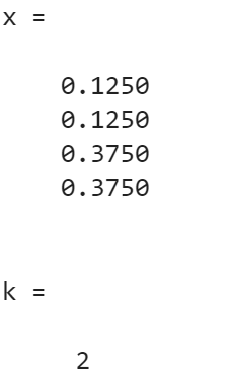

对比其他迭代法：

雅可比迭代（it_max=100,ep=1e−4）：

>> A = [4,-1,-1,0; -1,4,0,-1; -1,0,4,-1; 0,-1,-1,4];    b = [0,0,1,1]';    ep = 1e-4;
>> [x,k] = Jacobi(A,b,ep,it_max)

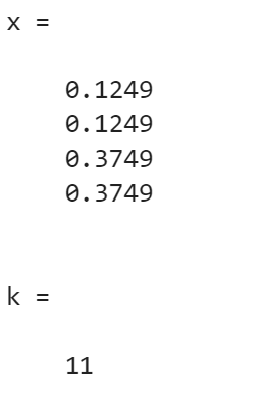
高斯 - 塞德尔迭代：

>> A = [4,-1,-1,0; -1,4,0,-1; -1,0,4,-1; 0,-1,-1,4];    b = [0,0,1,1]';    ep = 1e-4;
>> [x,k] = Gau_Seid(A,b,ep,it_max)

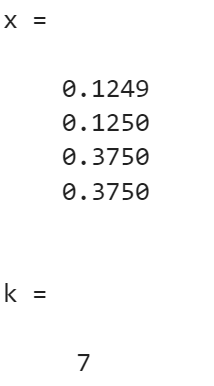
SOR 迭代（w=1.072）：

>> A = [4,-1,-1,0; -1,4,0,-1; -1,0,4,-1; 0,-1,-1,4];    b = [0,0,1,1]';    ep = 1e-4;
>> w = 1.072;
>> [x,k] = SOR(A,b,w,ep,it_max)

结论：共轭梯度法收敛最快，效率最高。

总结

本文介绍了四种求解线性方程组的迭代法：雅可比迭代法、高斯-塞德尔迭代法、逐次超松弛（SOR）迭代法和共轭梯度法。详细阐述了各算法的原理、分量公式及MATLAB实现步骤，并通过数值实验对比了其收敛性能。结果表明：雅可比法简单但收敛性较差；高斯-塞德尔法通过即时更新变量提高了效率；SOR法通过引入松弛因子（ω=1.1时最优）进一步加速收敛；共轭梯度法对对称正定矩阵收敛最快。实验数据验证了各方法的适用条件，为线性方程组求解提供了有效的迭代方案选择依据。

查看全文

http://www.dtcms.com/a/478716.html