条件概率、全概率、贝叶斯

概率的定义

• 描述性定义：将随机事件A发生的可能性大小（非负值）称为事件A发生的概率，记为。
• 统计性定义：在相同条件下做重复试验，事件A出现的次数K 和总的试验次数n 之比称为事件A在这n 次试验中出现的频率。当试验次数n 充分大时，频率将“稳定”于某常数p 。n 越大，频率偏离这个常数p 的可能性 越小 ，常数p 就称为事件A的概率。

条件概率

设A , B为任意事件，若P ( A ) > 0，在已知事件A发生的条件下，事件B发生的概率称为条件概率记为P ( B ∣ A ) ，即

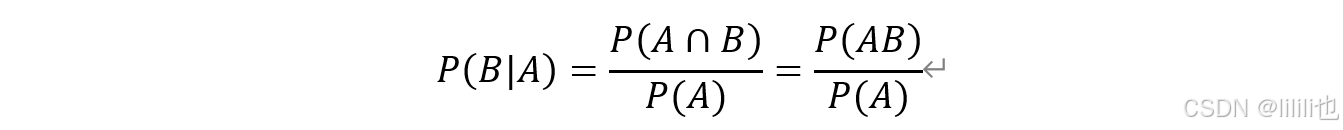
P ( B ∣ A ) 和P ( A ∣ B ) 代表的含义是不一样的，如下图所示

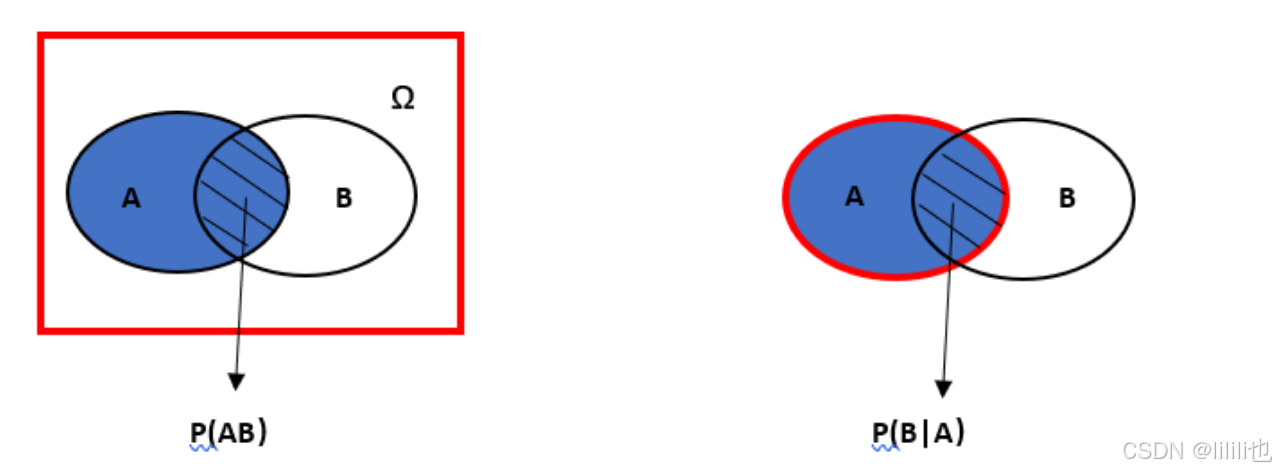
全概率

完备事件组：如果有限个事件满足，满足，且，则称有限个事件构成了一个完备事件组。

条件概率得乘法公式可得

对乘法公式进行推广，即对于任何正整数时，时，有。

全概率公式的意义在于执因索果，在于分解事件。

贝叶斯

贝叶斯的思想是执果索因，在知道结果的情况下去推断原因的可能性。