数据结构------二叉查找树

目录

什么是二叉查找树？

应用场景

二叉查找树参考实现

基本结构

插入结点过程

插入结点实现

初始化BST

查找结点过程

查找结点实现

查找最大值实现

查找最小值实现

---

什么是二叉查找树？

二叉查找树（Binary Search Tree），也称二叉排序树（Binary Sort Tree），简称BST。它是一种特殊的二叉树，具备以下特点：

• 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
• 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
• 左、右子树也分别为二叉排序树；

应用场景

叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛。
例如：在文件系统、数据库系统的索引等应用场景会采用这种数据结构进行高效率的排序与检索操作。

二叉查找树参考实现

基本结构

public class BinarySortTree {// 根节点TreeNode root;// 树节点内部类static class TreeNode {Integer data; // 节点数据TreeNode left; // 左子节点TreeNode right; // 右子节点TreeNode parent; // 父节点// 无参构造方法public TreeNode() {}// 有参构造方法public TreeNode(Integer val) {this.data = val;}}
}

插入结点过程

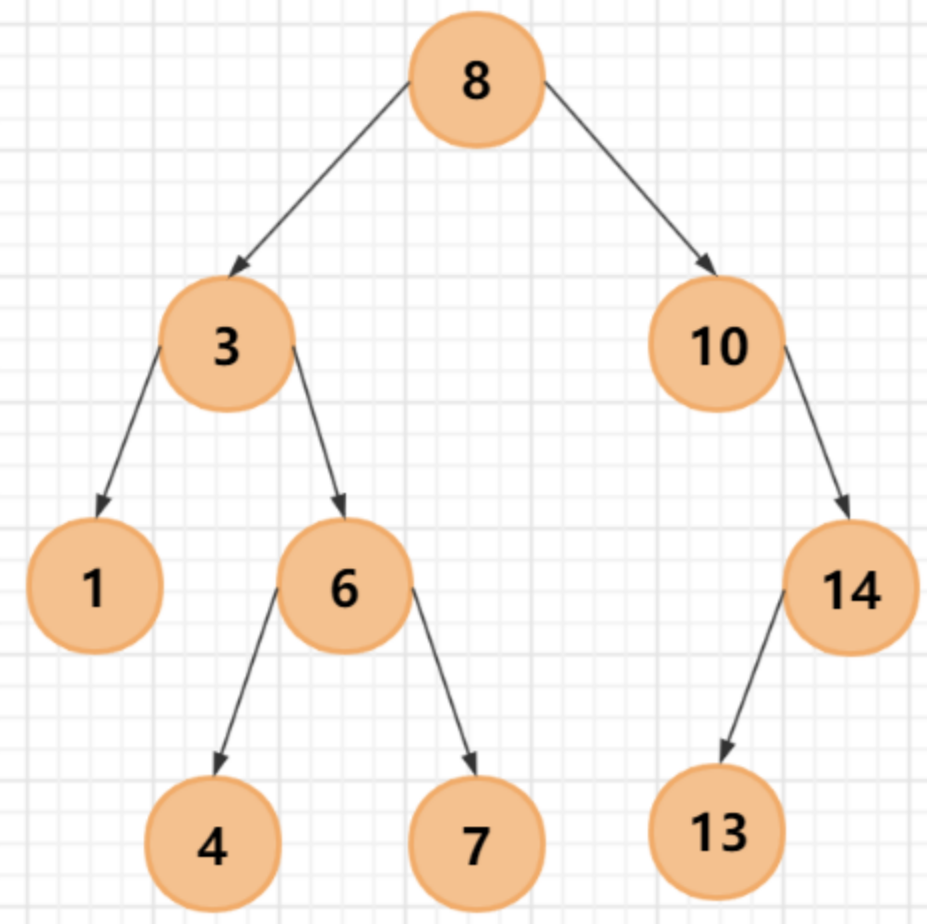
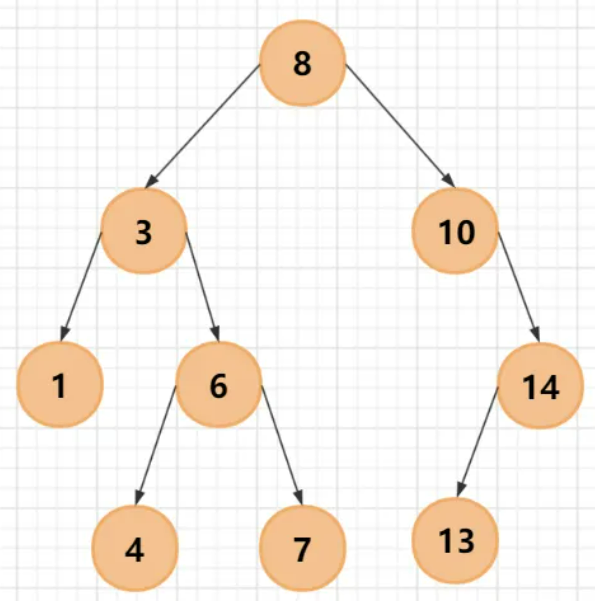
假设有无序数组：8、3、 10 、1、 6、 14、4、7、13，需要按照二叉查找树的方式进行存储。
结点插入过程如下：

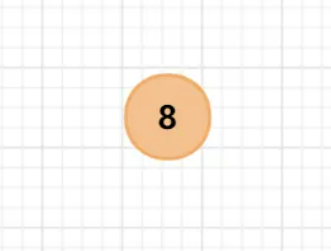
第一步：插入 8 作为根结点；

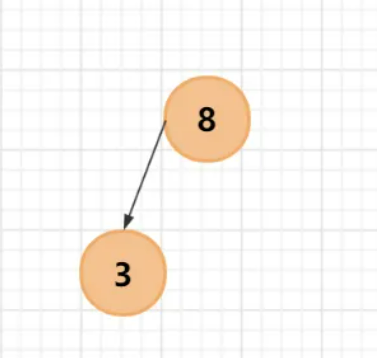
第二步：插入 3 ，与根结点 8 进行比较，发现比8小，且根结点没有左孩子，则将 3 插入到 8 的左孩子；

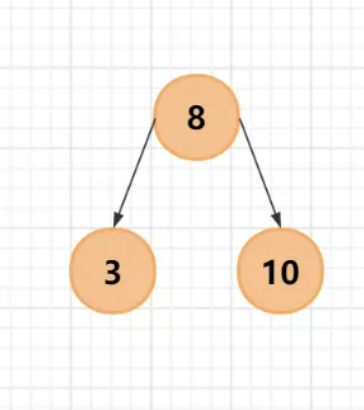
第三步：插入10，首先与根结点比较，发现比 8 大，则要将 10 插入根结点的右子树；根结点 8 的右子树为空，则将 10 作为 8 的右孩子；

插入 1，首先与根结点比较，比根结点小，则应插入根结点的左子树。再与根结点的左孩子 3 比较，发现比 3 还小，则应插入 3 的左孩子。

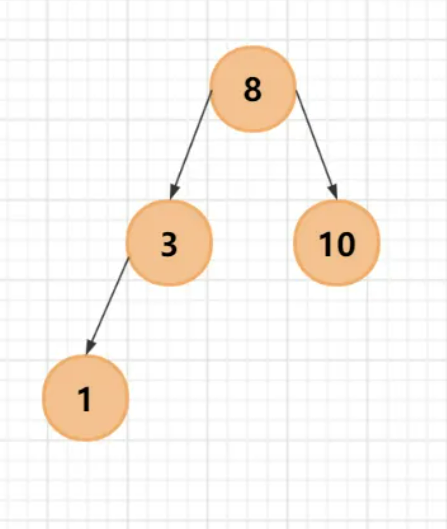
第五步：插入 6，先与根结点8比较，小于 8，向左走；再与 3 比较，大于 3，向右走，没有结点，则将6 作为3的右孩子；

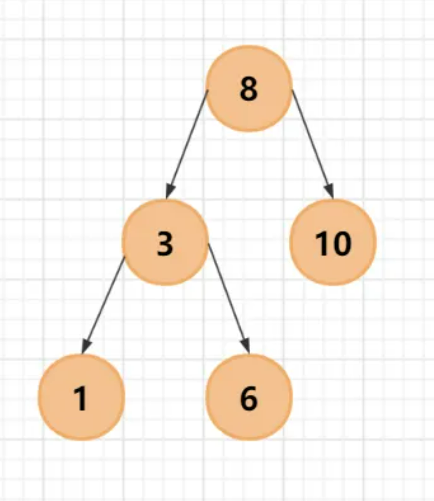
依此类推，二叉查找树最终完成初始化。

插入结点实现

// 插入新节点
public void insert(TreeNode newNode) {TreeNode currentNode = this.root; // 查找过程中的当前节点TreeNode parent = null;  // 新节点的父节点// 查找新节点的插入位置while (currentNode != null) {parent = currentNode;if (newNode.data < currentNode.data) {currentNode = currentNode.left;}else {currentNode = currentNode.right;}}// 设置新节点的父节点newNode.parent = parent;// 通过父节点的左右子节点属性，保存新节点if (parent == null) {this.root = newNode;} else {if (newNode.data < parent.data) {parent.left = newNode;}else {parent.right = newNode;}}
}

初始化BST

public void init(Integer[] numberArray) {for (int i = 0; i < numberArray.length; i++) {insert(new TreeNode(numberArray[i]));}
}

BinarySortTree bst = new BinarySortTree();
bst.init(new Integer[] { 8, 3, 10, 1, 6, 14, 4, 7, 13 });
bst.inOrder(bst.root);

• 数组中元素的原始顺序：8、3、10 、1、6、14、4、7、13
• 二叉排序树的中序遍历：1、3、4、6、7、8、10、13、14

查找结点过程

二叉排序树的查找操作基于二分查找，
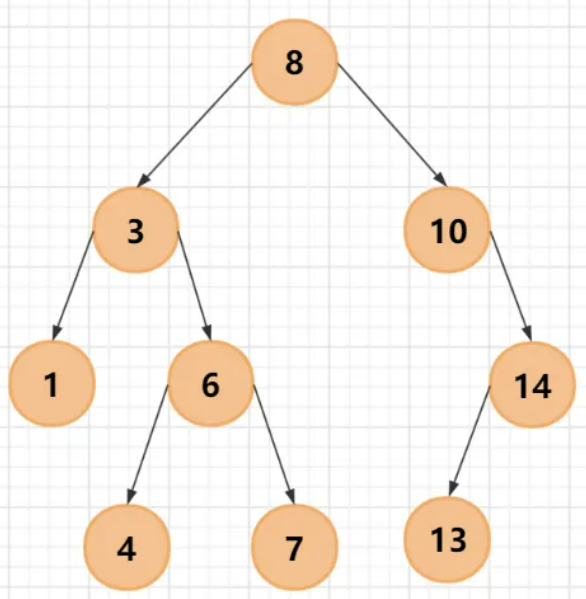
例如：在下面这颗二叉查找树中，查找值为13的结点的过程如下：

• 第一步：访问根结点 8
• 第二步：根据二叉排序树的左子树均比根结点小，右子树均比根结点大的性质， 13 > 8，因此值为13的结点可能在根结点 8 的右子树当中，我们查看根结点的右子结点 10
• 第三步：与第二步相似， 13 > 10，因此查看结点 10的右孩子 14
• 第四步：根据二叉排序树的左子树均比根结点小，右子树均比根结点大的性质， 13 < 14，因此查看 14的左孩子 13，找到目标结点

查找结点实现

private TreeNode search(TreeNode currentNode,Integer data) {if (currentNode == null) {return currentNode;}if (data < currentNode.data) {return search(currentNode.left, data);} else if (data > currentNode.data) {return search(currentNode.right, data);} else {return currentNode;}
}public TreeNode find(Integer data) {TreeNode resultNode = search(this.root, data);return resultNode;
}

查找最大值实现

public TreeNode findMax(TreeNode currentNode) {if(currentNode == null) {return currentNode;}TreeNode parent = null;  // 新节点的父节点// 查找新节点的插入位置while (currentNode != null) {parent = currentNode;currentNode = currentNode.right;}return parent;
}

查找最小值实现

// 查找最小值
public TreeNode findMin(TreeNode currentNode)  {if(currentNode == null) {return currentNode;}TreeNode parent = null;  // 新节点的父节点// 查找新节点的插入位置while (currentNode != null) {parent = currentNode;currentNode = currentNode.left;}return parent;
}