三大数学工具在深度学习中的本质探讨：从空间表示到动态优化

摘要

深度学习的强大泛化能力并非源于单一技术突破，而是线性代数、概率论与微积分三大数学工具协同作用的结果。本文从数学本质出发，剖析三者在深度学习中的核心定位——线性代数构建“空间表示与变换的骨架”，概率论提供“不确定性的量化标尺”，微积分赋予“动态优化的动力源”，并通过可视化流程与实例，揭示三者如何形成闭环，支撑从数据输入到模型收敛的全链路。

引言：深度学习的数学基石

当我们谈论深度学习时，往往聚焦于CNN、Transformer等网络结构，却忽略了其底层的数学逻辑：所有复杂模型都是三大数学工具的具象化载体。线性代数解决“数据如何被结构化表示”，概率论解决“模型如何量化不确定性与定义目标”，微积分解决“模型如何迭代优化”。三者并非孤立存在，而是通过“表示→评估→优化”的闭环，让深度学习具备处理图像、文本、语音等复杂任务的能力。

一、线性代数：深度学习的“空间骨架”

1.1 本质定位：结构化表示与维度变换

线性代数的核心是用向量/矩阵构建高维空间，并通过线性变换实现特征的层级提取。在深度学习中，原始数据（如图像、文本）必须先转化为线性代数可处理的结构化形式，才能被模型“理解”。

• 数据表示的本质：一张28×28的MNIST手写数字图像，本质是784维列向量（将像素按行/列展开）；一段文本的BERT Embedding，是768维向量（用数值编码语义信息）。这些向量并非随机排列，而是对应“像素空间”“语义空间”等特定高维空间的坐标。
• 特征变换的本质：卷积层、全连接层的核心是线性变换（矩阵乘法）。以全连接层为例，输入向量$\mathbf{x}\in {\mathbb{R}}^n$通过权重矩阵$\mathbf{W}\in {\mathbb{R}}^{m\times n}$与偏置$\mathbf{b}\in {\mathbb{R}}^m$，转化为输出$\mathbf{y}=\mathbf{W}\mathbf{x}+\mathbf{b}$，本质是将数据从$n$维输入空间映射到$m$维特征空间，实现“低阶特征（像素）→高阶特征（边缘、纹理、语义）”的提取。

1.2 深度学习中的典型应用

网络组件	线性代数操作	作用
卷积层	卷积核（小矩阵）与特征图（大矩阵）的互相关运算	提取局部空间特征
全连接层	权重矩阵与输入向量的乘法	整合全局特征
Batch Normalization	均值归一化与方差缩放（向量的线性变换）	加速训练收敛

1.3 可视化：数据的空间变换过程

上图展示MNIST分类任务中，数据通过线性变换从“像素空间”逐步映射到“类别特征空间”，最终输出10个类别的特征向量。

二、概率论：深度学习的“不确定性标尺”

2.1 本质定位：量化不确定性与定义优化目标

现实世界的信息存在天然不确定性（如传感器噪声、数据标注误差），概率论的核心是用数学模型描述不确定性，并将模糊的“任务需求”转化为可量化的优化目标。

• 不确定性的量化：深度学习模型的输出并非确定值，而是概率分布。例如，分类任务中Softmax层输出$\mathbf{p}=[p_1,p_2,...,p_{10}]$，其中$p_i=\frac{e^{y_i}}{{\sum }_{j=1}^{10}{e}^{y_j}}$，表示样本属于第$i$类的概率，本质是将输出向量转化为符合概率公理的分布。
• 优化目标的定义：损失函数是概率论在深度学习中的直接体现。以交叉熵损失为例，对于真实标签$\mathbf{y}$（独热向量）与预测分布$\mathbf{p}$，损失$L=-{\sum }_{i=1}^C{y}_i\log p_i$，本质是衡量“预测分布与真实分布的KL散度”，量化模型预测的“不合理程度”。

2.2 深度学习中的典型应用

任务类型	概率论工具	作用
分类任务	Softmax+交叉熵损失	输出类别概率并量化误差
目标检测	锚框的概率回归（Sigmoid）	判断锚框是否为目标
生成模型（GAN）	生成分布与真实分布的JS散度	衡量生成样本的真实性

三、微积分：深度学习的“动态优化动力源”

3.1 本质定位：求解梯度与驱动参数更新

深度学习模型的参数（如权重矩阵$\mathbf{W}$、偏置$\mathbf{b}$）初始时是随机值，需要通过迭代调整实现收敛。微积分的核心是通过链式法则计算损失函数对参数的梯度，为参数更新提供“方向与幅度”。

• 梯度的物理意义：对于损失函数$L(\mathbf{W},\mathbf{b})$，梯度$\nabla L=\left(\frac{\partial L}{\partial \mathbf{W}},\frac{\partial L}{\partial \mathbf{b}}\right)$表示“损失函数在当前参数点的最陡上升方向”。因此，参数更新需沿梯度反方向（$\mathbf{W}=\mathbf{W}-\eta \cdot \frac{\partial L}{\partial \mathbf{W}}$，$\eta$为学习率），即“梯度下降”。
• 反向传播的本质：深层网络的梯度计算依赖链式法则。以两层全连接网络为例，损失对第一层权重${\mathbf{W}}_1$的梯度$\frac{\partial L}{\partial {\mathbf{W}}_1}={\mathbf{x}}^T\cdot \frac{\partial L}{\partial {\mathbf{y}}_1}\cdot {\mathbf{W}}_2^T$，本质是将输出层的误差“反向传递”到输入层，逐层计算参数的梯度。

3.2 深度学习中的典型应用

优化场景	微积分工具	作用
参数更新	梯度下降（一阶导数）	调整权重以降低损失
学习率自适应（Adam）	一阶动量+二阶动量（梯度的统计特性）	平衡收敛速度与稳定性
网络剪枝	权重的梯度敏感性（二阶导数）	识别冗余参数

四、三大工具的协同机制：从数据到模型的闭环

三大数学工具并非独立工作，而是通过“数据表示→概率评估→梯度优化→参数更新→表示迭代”的闭环，支撑深度学习的端到端学习。其协同逻辑可通过以下流程图清晰呈现：

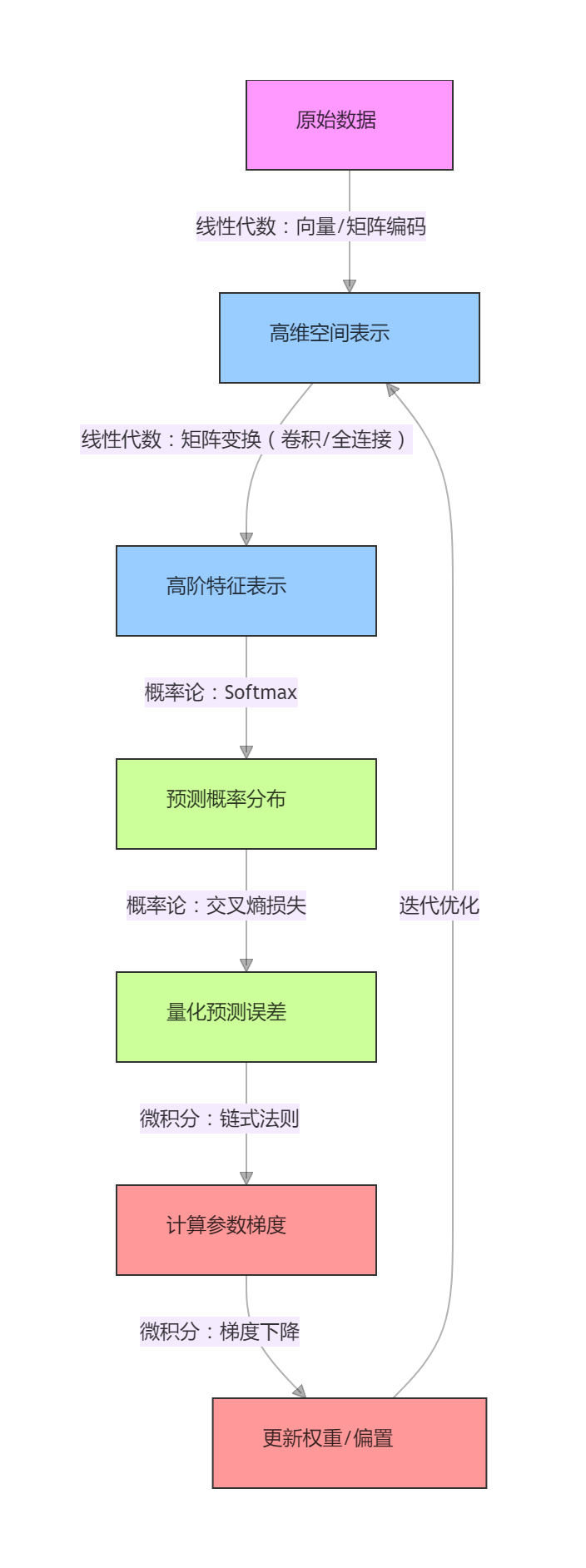
协同逻辑解析：

1. 线性代数将原始数据转化为可处理的特征表示，并通过层级变换提取有效信息；
2. 概率论将特征表示转化为概率分布，用损失函数量化模型性能，定义优化目标；
3. 微积分根据损失函数计算梯度，驱动参数更新，让线性代数的特征变换更贴合任务需求；
4. 更新后的参数重新作用于线性代数的特征表示，形成迭代闭环，直至模型收敛。

五、总结与展望

线性代数、概率论与微积分共同构成了深度学习的“数学三角”：线性代数是“骨架”，决定了数据的表示能力；概率论是“标尺”，量化了模型的不确定性与目标；微积分是“动力”，驱动了模型的迭代优化。三者的协同，让深度学习从“黑箱”走向“可解释的数学系统”。

未来，随着拓扑学（处理空间结构）、优化理论（提升求解效率）等数学工具的融入，深度学习的数学基础将进一步完善，为更复杂的自主智能任务（如机器人控制、通用人工智能）提供更强的理论支撑。理解三大工具的本质，是掌握深度学习核心逻辑、推动技术创新的关键第一步。