INT301 Bio-computation 生物计算(神经网络)Pt.1 导论与Hebb学习规则
文章目录
- 1. 导论
- 1.1 人工神经网络(ANN)
- 1.1.1 生物神经网络(Biological Neural Networks)
- 1.1.2 人工神经元(abstract neuron)
- 1.1.3 简单神经网络(Simple Neural Network)
- 1.1.4 人工神经网络(ANN)
- 1.1.5 机器学习
- 2. 人工神经网络
- 2.1 McCulloch-Pitts神经元(1943年)
- 2.2 人工神经网络(ANN)的学习规则
- 2.2.1 Hebb规则
1. 导论
生物计算是一个致力于使用模仿自然界原理的计算方法来解决复杂问题的领域。其目标是开发出具有更强鲁棒性、可扩展性、灵活性和可靠性的信息处理工具。
它是一个多学科交叉领域,主要基于生物学、计算机科学、信息学、认知科学和机器人学。而本课程主要内容是人工神经网络。
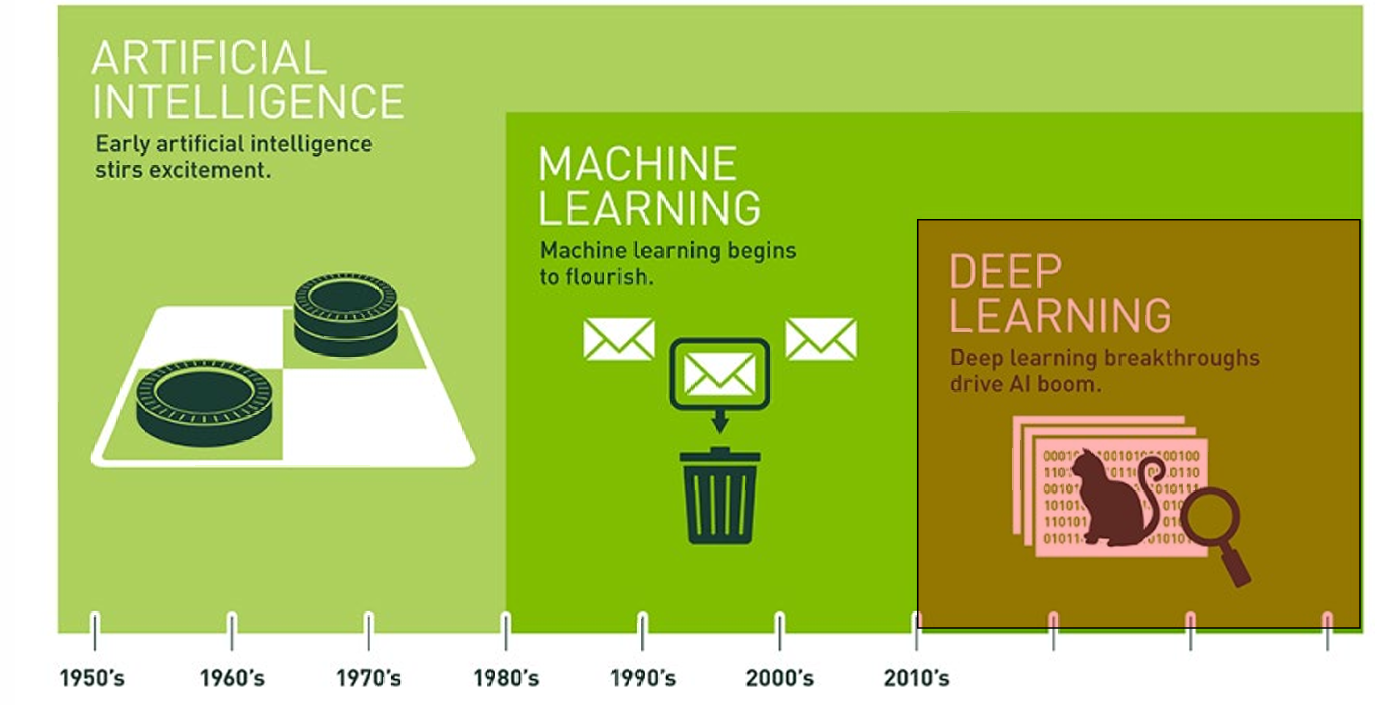
深度学习是机器学习的一部分,机器学习是人工智能的一部分。
人工智能是一个广义的概念,泛指所有让计算机表现出“智能”的技术,比如语音识别、图像识别、下棋、对话等。
机器学习是AI的一部分,核心思想是让机器从数据中学习规律,而不是靠人一条条编程规则。比如通过大量图片训练模型识别猫和狗。
神经网络——也称为“人工”神经网络——是一种机器学习方式,粗略地(loosely)模仿了大脑中神经元的工作方式。
深度学习——机器学习的一个子集,使得多层神经网络的计算变得可行。
1.1 人工神经网络(ANN)
早期一些研究者曾尝试用“神经元模型”来做人工智能。当经典 AI(符号推理)的局限性暴露后,采用新模型、新算法的 ANN 开始显现价值。70-80 年代,专家系统遇冷(知识获取瓶颈、组合爆炸)。同期,反向传播(BP, 1986)被重新发现,多层感知机可解决非线性问题,ANN 迎来第一次复兴。
ANN 诞生 50 多年前,人们对真实神经元如何工作几乎一无所知。最早的 ANN 只是借用“神经元”这个名词和极粗略的“输入-加权-求和-阈值-输出”概念,并未依据真实生物机制。此后,神经科学在解剖和生理层面取得巨大进展,但 ANN 的基本结构却几乎没变。今天我们已经知道:生物神经元有树突棘、轴突初始段、脉冲发放、离子通道、可塑性规则(STDP、Hebb 等),而主流 ANN 仍是“连续值输入→矩阵乘法→非线性激活”这一 1950 年代框架。
因此,尽管名字叫“神经网络”,ANN 的设计与真实神经元几乎毫无共同之处。但ANN 的重点不再追求“生物逼真”,而是追求“从数据里学习”。
因此,简单神经网络相比经典 AI 的最大优势就是:它们从数据里学,不需要人类专家一条条写规则。
如今 ANN 只是机器学习这个大篮子里的一个工具,其它还有大量数学/统计方法。
包括 ANN 在内的机器学习技术,都是看海量数据、提取统计规律、然后把结果做分类/预测。
机器学习的三步骤可以概括为:1.大数据 → 2. 统计/优化 → 3. 模型输出(分类、回归、聚类、生成等)。
ANN 只是用“可微分网络”这种方式完成第 2 步。
人脑是一个智能系统。通过研究脑如何运作,我们能弄清“智能”究竟是什么,以及任何智能系统都必须具备哪些脑特性。
目前的研究指出:
记忆本质上是模式序列(而非随机存取的地址);
行为/动作是所有学习不可或缺的环节;
学习必须是连续、在线的,而非批量一次性。
此外,生物神经元远比简单神经网络里用的“神经元”复杂得多。
1.1.1 生物神经网络(Biological Neural Networks)
人脑的内部运作通常被建模为“神经元”以及由神经元组成的网络,这些网络被称为生物神经网络。
据估计,人脑大约包含1000亿个神经元,它们在这些网络中通过路径互相连接。
神经元之间通过一个接口进行通信:一个神经元的轴突末梢与另一个神经元的树突之间有一个间隙(称为突触)。
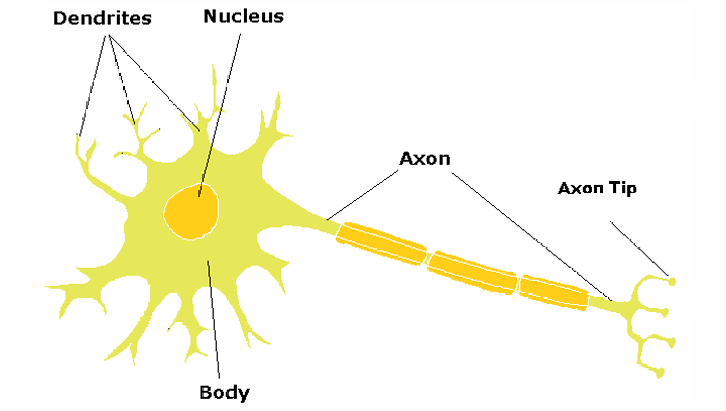
轴突(axon):像电缆一样把信号传出去;
轴突末梢(axon terminal):信号输出端;
树突(dendrite):接收信号的部分;
突触(synapse):两个神经元之间的“间隙”,信号通过化学物质(神经递质)在这里传递。
1.1.2 人工神经元(abstract neuron)
一个神经元会把“消息”传给下一个神经元。
前提条件是:前面所有神经元传过来的信号,各自先乘一个权重(weight),再加总(summation);如果加起来的值超过某个门槛值(threshold),才算“够格”。
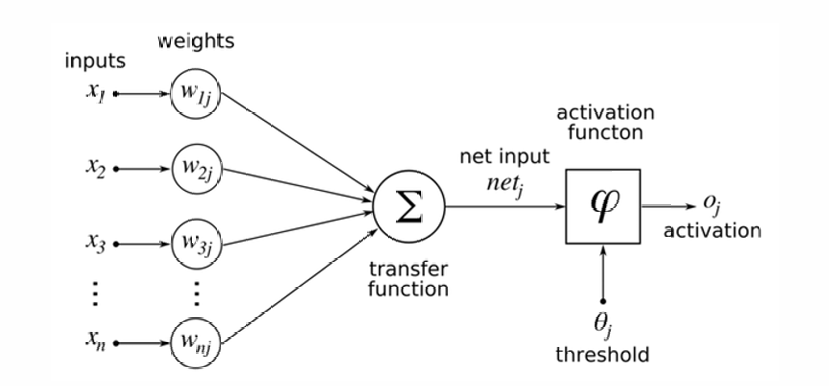
一旦超过门槛,就触发激活(activation),消息继续往下一层传;否则就“沉默”,不往外发信号。
1.1.3 简单神经网络(Simple Neural Network)
神经网络是受人类大脑启发而设计出来的数学模型,其工作流程可以分成两个截然不同的阶段。
第一阶段是学习/训练阶段:模型通过喂给它的数据,自动调节内部权重,学会完成某项具体任务。
第二阶段是应用/推理阶段:训练好的模型被部署到实际场景,接受新输入并给出结果,不再(或极少)更新权重。
1.1.4 人工神经网络(ANN)
在生物系统中,学习涉及到神经元之间突触连接的调整。人工神经网络(ANN)也是如此,通过调整网络中“人工神经元”之间的连接权重来进行学习。
神经网络可以通过训练来执行各种任务,例如:
- 预测或预报(如股票价格预测、天气预报)
- 模式识别(如图像识别、语音识别)
- 数据分类(如垃圾邮件过滤、疾病诊断)
1.1.5 机器学习
这里也可以参考INT305。
学习:通过学习、指导或经验获得知识、理解或技能。
机器学习:机器学习指的是系统的变化,这些变化是适应性的,因为它们使系统能够在下一次更有效地完成相同的任务或从相同人群中抽取的任务。(系统通过适应性变化来提高处理相同或相似任务的效率。)
机器学习的优势如下:
- 可以用于人类专业知识不存在的领域。
- 可以用于人类无法解释其专业知识的复杂任务。
- 可以用于解决方案随时间变化的动态问题。
- 可以用于需要个性化解决方案的特定情况。
机器学习主要有两个阶段:
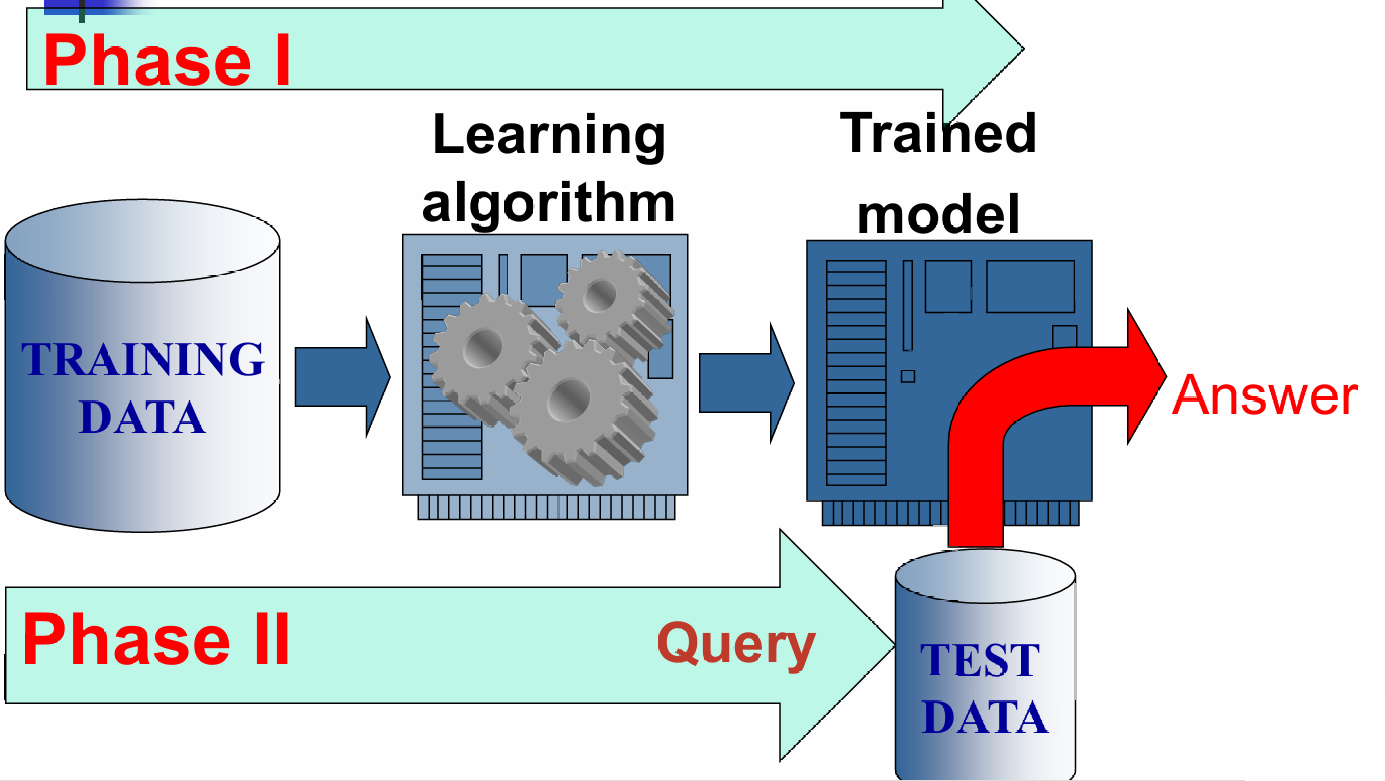
- 训练阶段,使用训练数据通过学习算法来训练模型。
- 测试阶段,使用测试数据来评估训练好的模型的性能。
2. 人工神经网络
前文提过人工神经网络的基本组成:
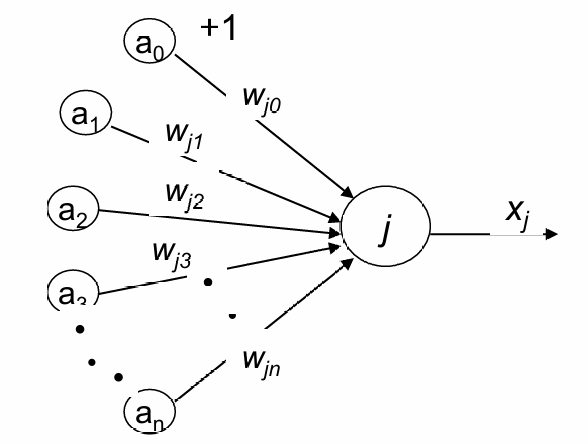
- 输入(Inputs):
每个输入iii传递一个实数值aia_iai。
这些输入可以代表不同的特征或信号。 - 权重(Weights):
每个连接被赋予一个权重 wijw_{ij}wij,其中iii是输入的索引,jjj是神经元的索引。
权重决定了每个输入对神经元输出的影响程度。 - 偏置(Bias):
偏置项a0a_0a0(通常加1表示)允许模型在没有输入信号时也能激活。
偏置与权重wj0w_{j0}wj0相乘,影响神经元的激活。 - 总输入(Total Input):
总输入SSS是所有输入与对应权重乘积的和,即S=∑i=0nwji⋅aiS = \sum_{i=0}^{n} w_{ji} \cdot a_iS=∑i=0nwji⋅ai。
这个总和与阈值进行比较。 - 阈值(Threshold):
在这个模型中,阈值被设定为0。
总输入SSS与阈值比较,决定是否激活神经元。 - 输出(Output):
如果总输入SSS超过阈值,神经元被激活,产生输出XjX_jXj。
输出可以是激活函数的结果,如阶跃函数、Sigmoid函数等。
2.1 McCulloch-Pitts神经元(1943年)
1943年,Warren Sturgis McCulloch和Walter Pitts提出的McCulloch-Pitts神经元模型将神经元建模为一个二进制离散时间元素,其具有兴奋性和抑制性输入以及一个兴奋阈值。由这样的元素组成的网络是第一个将神经网络研究与现代意义上的计算概念联系起来的模型。
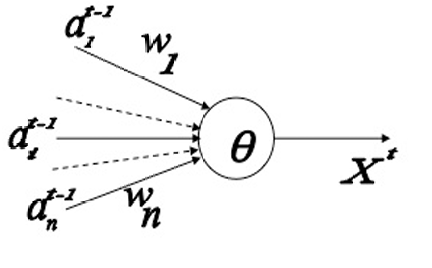
来自第iii个突触前神经元的输入值aita_i^tait在任何时刻ttt只能取两个值:0 或 1。
连接的权重wiw_iwi有两种类型:
+1 表示兴奋性(excitatory)连接,即这种连接会增加神经元激活的可能性。
−1 表示抑制性(inhibitory)连接,即这种连接会减少神经元激活的可能性。
与神经元相关联的有一个兴奋阈值θθθ。
只有当加权输入的总和超过这个阈值时,神经元才会激活并产生输出XtX^tXt。
神经元在下一个时刻t+1t+1t+1的输出xt+1x ^{t+1}xt+1根据以下规则定义:
xt+1=1x^{t+1} = 1 \quadxt+1=1当且仅当St=∑iwiait≥θ\quad S^t = \sum_i w_i a_i^t \geq \thetaSt=∑iwiait≥θ
总输入StS^tSt是所有输入aita_i^tait与其对应权重wiw_iwi 的乘积之和:St=∑iwiaitS^t = \sum_i w_i a_i^tSt=∑iwiait
在MP神经元中,我们将时刻ttt的总输入StS^tSt称为神经元的即时状态(instant state)。
MP神经元的状态StS^tSt不依赖于神经元自身的先前状态,而是简单地由当前输入决定。
St=∑iwiait=f(t)S^t = \sum_i w_i a_i^t=f(t)St=∑iwiait=f(t)
神经元的输出xt+1x^{t+1}xt+1是其状态StS^tSt的函数,因此输出也可以表示为离散时间的函数:x(t)=g(St)=g(f(t))x(t) = g(S^t) = g(f(t))x(t)=g(St)=g(f(t))
这里ggg是阈值激活函数(threshold activation function),StS^tSt是神经元在时刻ttt的总输入,f(t)f(t)f(t)是总输入的函数。
阈值激活函数g(St)g(S^t)g(St)可以表示为:g(St)=H(St−θ)={1,if St≥θ;0,if St<θ.g(S^t) = H(S^t - \theta) = \begin{cases} 1, & \text{if } S^t \geq \theta; \\ 0, & \text{if } S^t < \theta. \end{cases}g(St)=H(St−θ)={1,0,if St≥θ;if St<θ.
这里,HHH是Heaviside(单位阶跃)函数,θθθ是阈值。
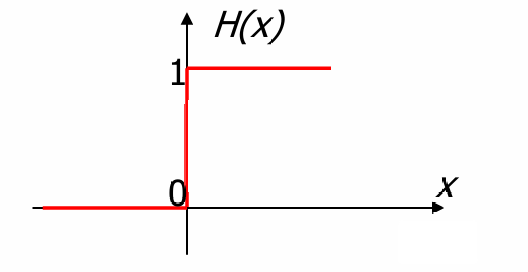
Heaviside函数 H(X) 定义为:H(X)={1,if X≥0;0,if X<0.H(X) = \begin{cases} 1, & \text{if } X \geq 0; \\ 0, & \text{if } X < 0. \end{cases}H(X)={1,0,if X≥0;if X<0.
这个函数在X≥0X≥0X≥0时输出1,在X<0X<0X<0时输出0。
M-P神经元为一种机器(单元网络)奠定了基础,这种机器能够存储信息,并且执行逻辑和算术运算。
2.2 人工神经网络(ANN)的学习规则
在模拟了大脑存储信息和执行逻辑/算术运算的能力之后,ANN的下一个发展目标是模拟大脑通过经验学习新知识的能力。
学习意味着根据经验而改变。在前面,由McCulloch-Pitts(M-P)神经元组成的网络中,连接的二进制权重和阈值是固定的。
唯一可能的改变是连接模式的改变,这在技术上是昂贵的。需要一些容易改变的自由参数。
因此变为我们前文所提到的样子。

理想的自由参数是连接权重 wjiw_{ji}wji,通过调整这些权重,可以在不改变连接模式的情况下实现学习。
总输入SjS_jSj是所有输入aia_iai与其对应权重wjiw_{ji}wji的乘积之和:
Sj=∑i=0nwjiaiS_j = \sum_{i=0}^{n} w_{ji} a_iSj=∑i=0nwjiai
神经元的输出xjx_jxj取决于总输入SjS_jSj是否超过阈值:
xj={0,if Sj≤01,if Sj>0x_j = \begin{cases} 0, & \text{if } S_j \leq 0 \\ 1, & \text{if } S_j > 0 \end{cases}xj={0,1,if Sj≤0if Sj>0
学习规则的核心目的,即通过调整网络中神经元之间连接的权重来优化网络的输出,使其达到预期的效果。
人工神经网络中的许多工作都集中在定义如何改变神经元之间连接的权重的学习规则上,以更好地使网络适应并服务于某些整体功能。
在实验神经科学有限的时期,这些学习规则的经典定义并非来自生物学,而是来自Donald Hebb和Frank Rosenblatt的心理研究。Hebb提出,突触连接强度的特定类型使用依赖性修改可能是神经系统学习的基础。
2.2.1 Hebb规则
Hebb规则,也被称为“一起发射就一起连接”(fire together, wire together),是神经科学中关于学习和记忆形成的基本理论之一。根据Hebb的假设,如果两个神经元经常同时被激活,它们之间的突触连接就会加强。这种连接的加强被认为是学习和记忆的神经基础。
具体来说,当神经元A的轴突足够接近神经元B,并且反复参与激发B时,会导致A和/或B发生一些生长或代谢变化,从而增加A激发B的效率。这种效率的增加被认为是学习和记忆形成过程中的关键机制。
Hebb规则的基本思想是,如果两个神经元经常一起激活,它们之间的连接权重应该增加。这种权重的增加可以通过以下数学公式来实现:
wjik+1=wjik+Δwjikw_{ji}^{k+1} = w_{ji}^k + \Delta w_{ji}^kwjik+1=wjik+Δwjik
其中:wjik+1w_{ji}^{k+1}wjik+1是在随后时刻k+1k+1k+1的连接权重。
wjikw_{ji}^{k}wjik是在时刻kkk的连接权重。
Δwjik\Delta w_{ji}^kΔwjik是权重的变化量,通过如下公式进行计算:
Δwjik=Caikxjk\Delta w_{ji}^k = C a_i^k x_j^kΔwjik=Caikxjk
其中:CCC是一个常数,用于控制学习速率。
aika_i^kaik是是在时刻kkk来自突触前神经元的输入值。
xjkx_j^kxjk是神经元jjj在第kkk次迭代时的输出。
因此,只有在通过该连接的先前输入和由此产生的输出同时不为0的情况下,连接的权重才会在下一个时刻发生变化。
方程强调了Hebbian突触的关联性。
Hebb的原始学习规则专门针对兴奋性突触,它只能增加权重,而不能减少权重。因此会网络中神经元之间的差异性减小,因为所有权重都会趋向于增加。当权重增加到一定程度时,它们可能会达到饱和点,这意味着进一步增加权重对神经元的激活没有额外的影响。
然而,当Hebb规则通过一个形式化规则扩展时,例如,保持给定神经元上所有突触的总强度不变,它倾向于即使没有外部指导(如监督学习中的标签),神经元也能通过这种规则自我调整,以更好地响应某些输入模式。由于这个原因,Hebb规则在许多人工神经网络算法的研究中扮演着重要角色,例如无监督学习或自组织,我们将在后面学习这些内容。
我们看一个例子。
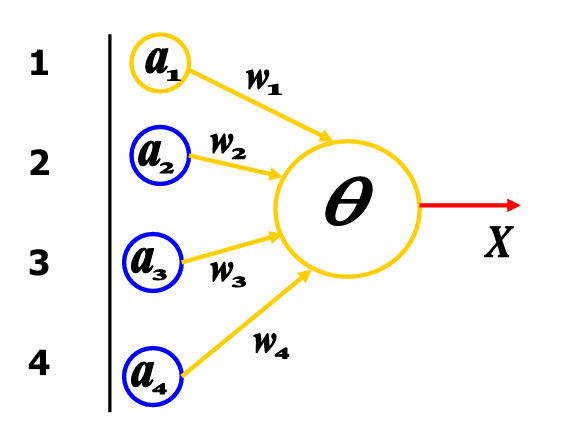
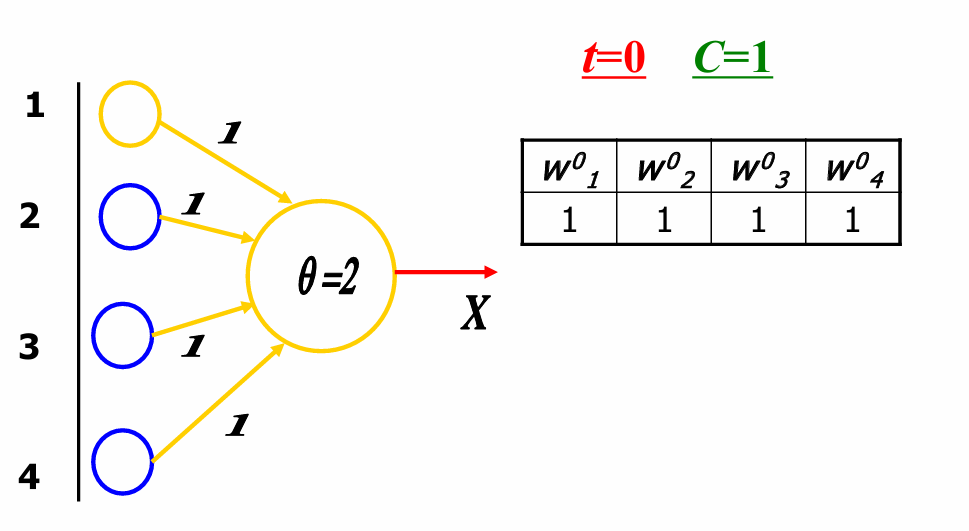
权重矩阵W0W^0W0在t=0t=0t=0时初始化为全1,即wj10=wj20=wj30=wj40=1w_{j1}^0=w_{j2}^0=w_{j3}^0=w_{j4}^0=1wj10=wj20=wj30=wj40=1。学习率CCC设置为1。阈值θθθ设置为2。神经元的输出XXX取决于总输入SjS_jSj是否超过阈值。
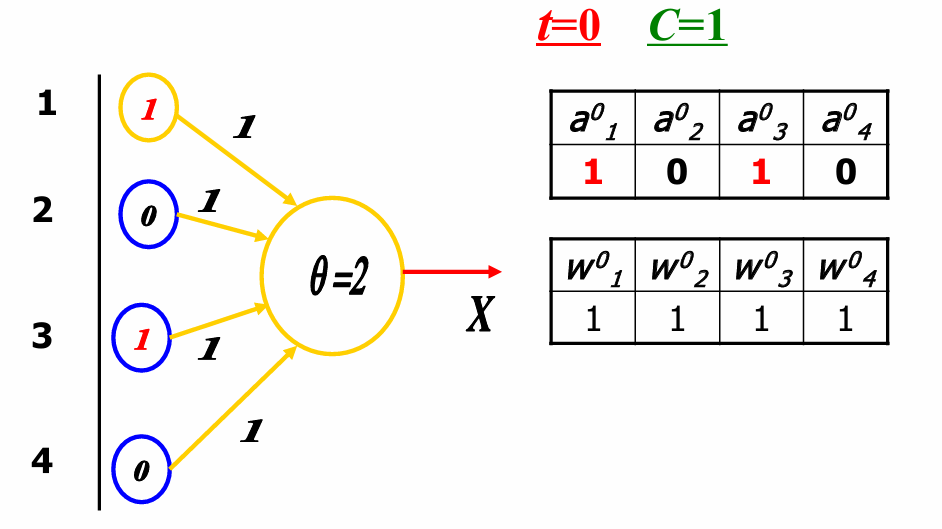
现在输入单元的值分别为1, 0, 1, 0。
权重矩阵W0W^0W0在t=0t=0t=0时初始化为全1。
总输入S0S^0S0的计算公式为:S0=∑i=14ai0×wi0=a10×w10+a20×w20+a30×w30+a40×w40=1×1+0×1+1×1+0×1=2≥θS^0 = \sum_{i=1}^{4} a_i^0 \times w_i^0 = a_1^0 \times w_1^0 + a_2^0 \times w_2^0 + a_3^0 \times w_3^0 + a_4^0 \times w_4^0 = 1 \times 1 + 0 \times 1 + 1 \times 1 + 0 \times 1 = 2 ≥ θS0=∑i=14ai0×wi0=a10×w10+a20×w20+a30×w30+a40×w40=1×1+0×1+1×1+0×1=2≥θ
这里总输入的结果大于阈值。因此神经元的输出X0=1X^0=1X0=1
现在根据Hebb学习规则,权重更新如下:
Δwi0=Cai0X0\Delta w_i^0 = C a_i^0 X^0Δwi0=Cai0X0
代入具体数值:
Δw10=1×1×1=1,Δw20=1×0×1=0,Δw30=1×1×1=1,Δw40=1×0×1=0\Delta w_1^0=1×1×1=1,\Delta w_2^0=1×0×1=0,\Delta w_3^0=1×1×1=1,\Delta w_4^0=1×0×1=0Δw10=1×1×1=1,Δw20=1×0×1=0,Δw30=1×1×1=1,Δw40=1×0×1=0
更新后的权重:
w11=w10+Δw10=1+1=2,w21=w20+Δw20=1+0=1,w31=w10+Δw30=1+1=2,w41=w40+Δw40=1+0=1w_1^1=w_1^0+\Delta w_1^0=1+1=2,w_2^1=w_2^0+\Delta w_2^0=1+0=1,w_3^1=w_1^0+\Delta w_3^0=1+1=2,w_4^1=w_4^0+\Delta w_4^0=1+0=1w11=w10+Δw10=1+1=2,w21=w20+Δw20=1+0=1,w31=w10+Δw30=1+1=2,w41=w40+Δw40=1+0=1
然后我们准备开始新的一轮迭代。
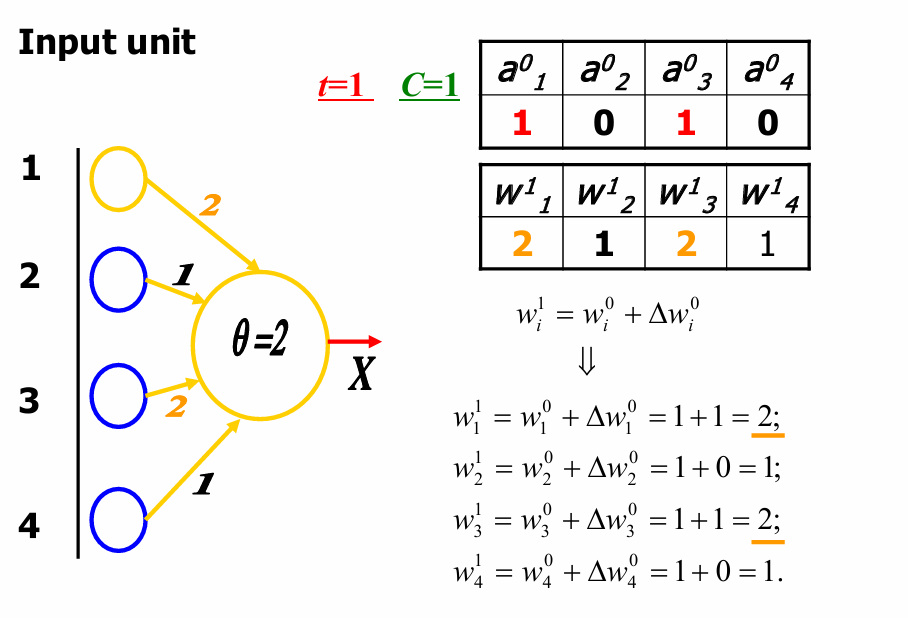
这时候t=1t=1t=1,权重矩阵变为W1W^1W1,现在我们要计算新的总输入S1S^1S1和相应的输出X1X^1X1。
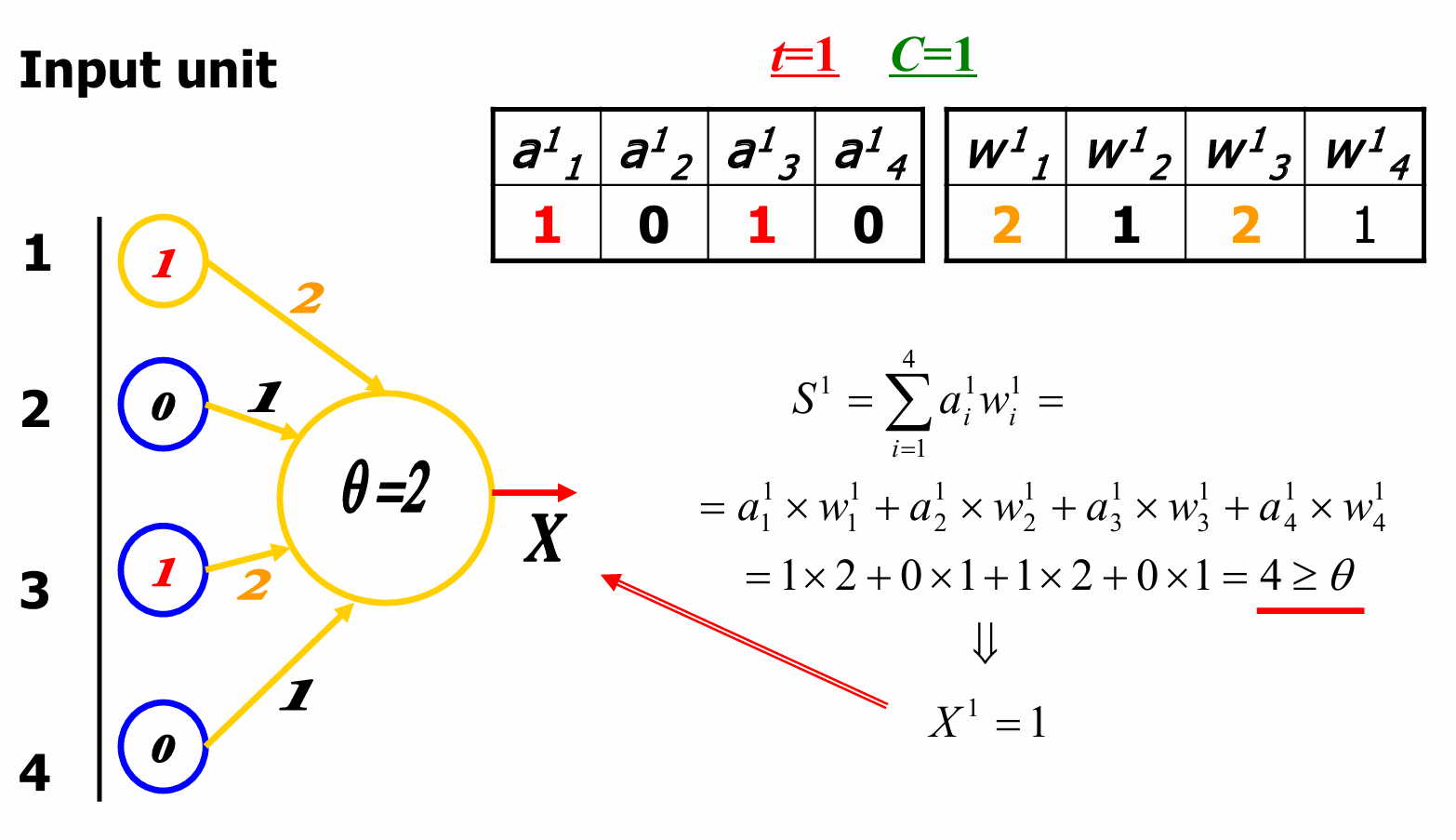
我们根据原来的输入单元的值和新的权重矩阵进行计算:
S1=∑i=14ai1wi1=a11×w11+a21×w21+a31×w31+a41×w41=1×2+0×1+1×2+0×1=4≥θS^1 = \sum_{i=1}^{4} a_i^1 w_i^1 = a_1^1 \times w_1^1 + a_2^1 \times w_2^1 + a_3^1 \times w_3^1 + a_4^1 \times w_4^1=1×2+0×1+1×2+0×1=4 ≥ θS1=∑i=14ai1wi1=a11×w11+a21×w21+a31×w31+a41×w41=1×2+0×1+1×2+0×1=4≥θ
这里总输入的结果大于阈值。因此神经元的输出X1=1X^1=1X1=1
现在根据Hebb学习规则,权重更新如下:
Δwi1=Cai1X1\Delta w_i^1 = C a_i^1 X^1Δwi1=Cai1X1
代入具体数值:
Δw11=1×1×1=1,Δw21=1×0×1=0,Δw31=1×1×1=1,Δw41=1×0×1=0\Delta w_1^1=1×1×1=1,\Delta w_2^1=1×0×1=0,\Delta w_3^1=1×1×1=1,\Delta w_4^1=1×0×1=0Δw11=1×1×1=1,Δw21=1×0×1=0,Δw31=1×1×1=1,Δw41=1×0×1=0
更新后的权重:
w12=w11+Δw11=2+1=3,w22=w21+Δw21=1+0=1,w32=w11+Δw31=2+1=3,w42=w41+Δw41=1+0=1w_1^2=w_1^1+\Delta w_1^1=2+1=3,w_2^2=w_2^1+\Delta w_2^1=1+0=1,w_3^2=w_1^1+\Delta w_3^1=2+1=3,w_4^2=w_4^1+\Delta w_4^1=1+0=1w12=w11+Δw11=2+1=3,w22=w21+Δw21=1+0=1,w32=w11+Δw31=2+1=3,w42=w41+Δw41=1+0=1
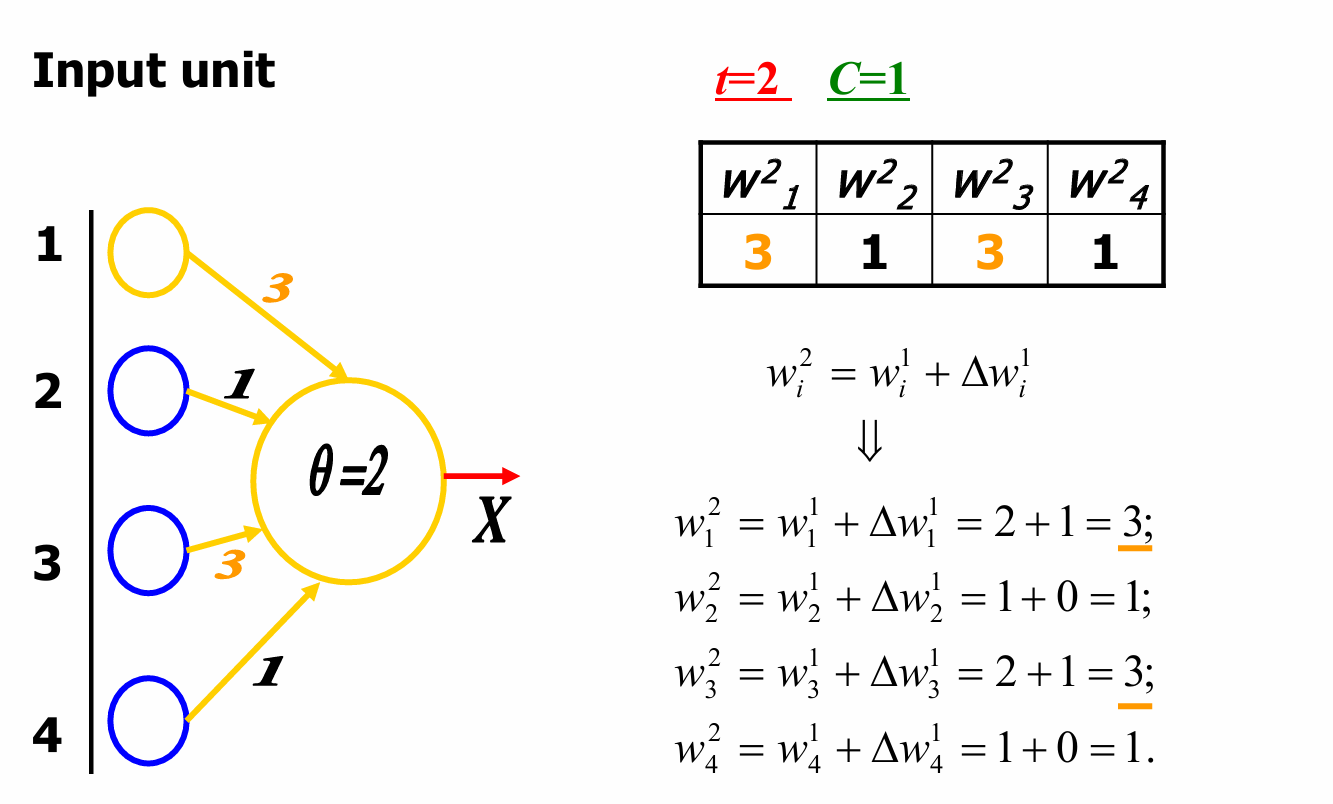
我们现在进入下一轮迭代。
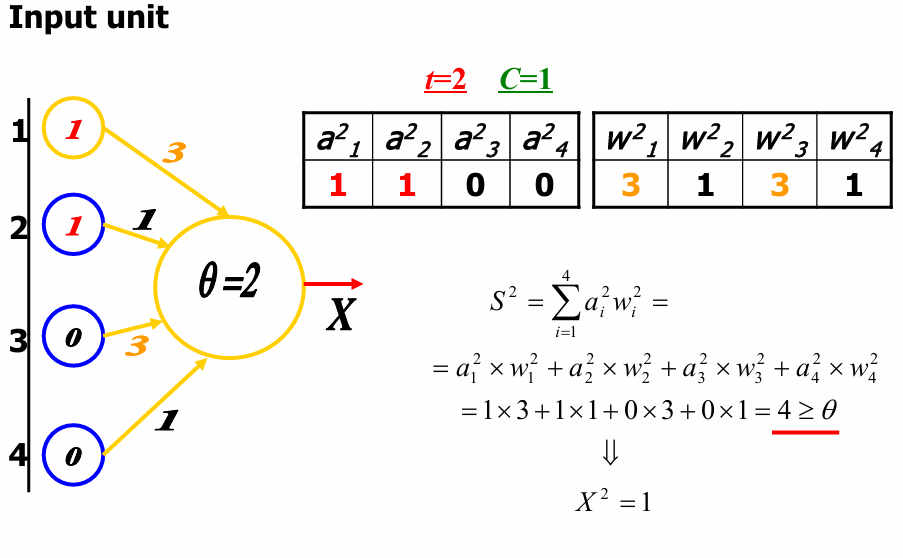
现在输入单元的值分别为1, 1, 0, 0。
权重矩阵W2W^2W2更新为:w12=3,w22=1,w32=3,w42=1w_1^2=3,w_2^2=1,w_3^2=3,w_4^2=1w12=3,w22=1,w32=3,w42=1
所以总输入S2S^2S2的计算如下:S2=∑i=14ai2wi2=a12×w12+a22×w22+a32×w32+a42×w42=1×3+1×1+0×3+0×1=4≥θS^2 = \sum_{i=1}^{4} a_i^2 w_i^2 = a_1^2 \times w_1^2 + a_2^2 \times w_2^2 + a_3^2 \times w_3^2 + a_4^2 \times w_4^2=1×3+1×1+0×3+0×1=4≥ θS2=∑i=14ai2wi2=a12×w12+a22×w22+a32×w32+a42×w42=1×3+1×1+0×3+0×1=4≥θ
这里总输入的结果大于阈值。因此神经元的输出X2=1X^2=1X2=1
现在根据Hebb学习规则,权重更新如下:
Δwi2=Cai2X2\Delta w_i^2 = C a_i^2 X^2Δwi2=Cai2X2
代入具体数值:
Δw12=1×1×1=1,Δw22=1×1×1=1,Δw32=1×0×1=0,Δw42=1×0×1=0\Delta w_1^2=1×1×1=1,\Delta w_2^2=1×1×1=1,\Delta w_3^2=1×0×1=0,\Delta w_4^2=1×0×1=0Δw12=1×1×1=1,Δw22=1×1×1=1,Δw32=1×0×1=0,Δw42=1×0×1=0
更新后的权重:
w13=w12+Δw12=3+1=4,w23=w22+Δw22=1+1=2,w33=w12+Δw32=3+0=3,w43=w42+Δw42=1+0=1w_1^3=w_1^2+\Delta w_1^2=3+1=4,w_2^3=w_2^2+\Delta w_2^2=1+1=2,w_3^3=w_1^2+\Delta w_3^2=3+0=3,w_4^3=w_4^2+\Delta w_4^2=1+0=1w13=w12+Δw12=3+1=4,w23=w22+Δw22=1+1=2,w33=w12+Δw32=3+0=3,w43=w42+Δw42=1+0=1
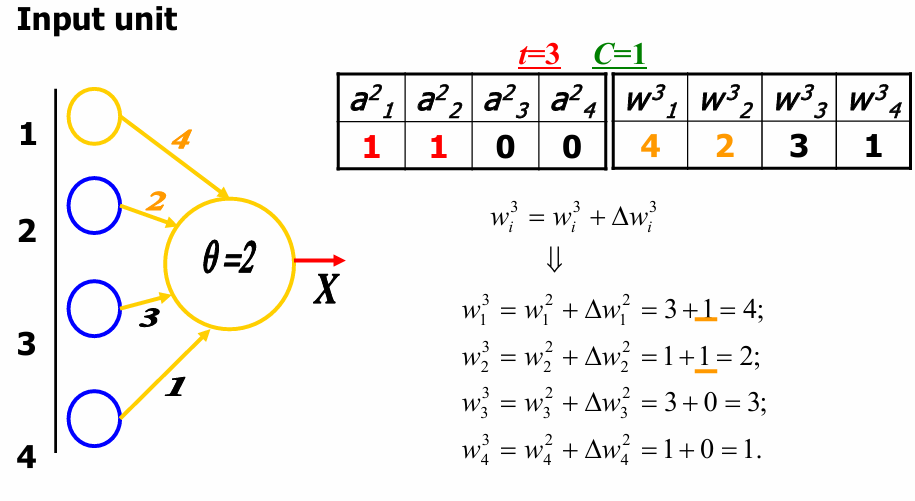
以此继续往下。
这便是Hebb学习规则。
