算法基础 典型题 堆

算法基础练习总结入口：我的算法地图

一、基本概念

1、堆（Heap）：是一种基于完全二叉树的数据结构，核心特性是 “堆序性”。 最大堆（或大顶堆） 父节点值 ≥ 子节点值；最小堆（或小顶堆）父节点值 ≤ 子节点值。堆的优势在于能高效获取和维护 “极值”（最大值或最小值），插入、删除操作的时间复杂度为 O (log n)，是解决 “优先级处理、Top K 问题、动态中位数” 等场景的核心工具。
典型结构：完全二叉树（除最后一层外，每层节点全满；最后一层节点靠左排列），通常用数组实现（节省空间，便于索引计算）。索引关系（数组下标i）：左孩子：2i + 1，右孩子：2i + 2，父节点：(i - 1) // 2。

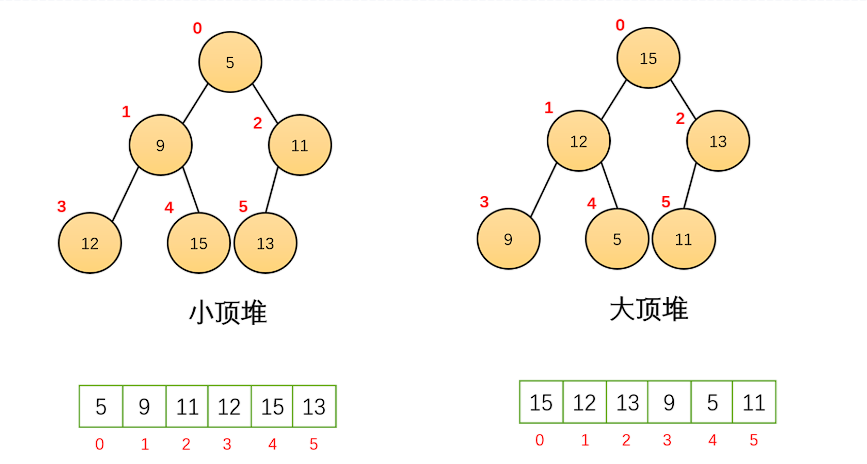
2、堆排序：一种基于堆（Heap） 数据结构的高效排序算法，核心利用堆的 “堆序性”（最大堆的根节点是最大值，最小堆的根节点是最小值），通过 “建堆→提取堆顶→调整堆” 的循环，将无序数组逐步转换为有序数组。其时间复杂度稳定为O(n log n)，且是原地排序（仅需 O (1) 额外空间），在需要稳定高效排序的场景中广泛应用。和几个典型快排算法比较：

二、场景分析

1、典型题目类型总结

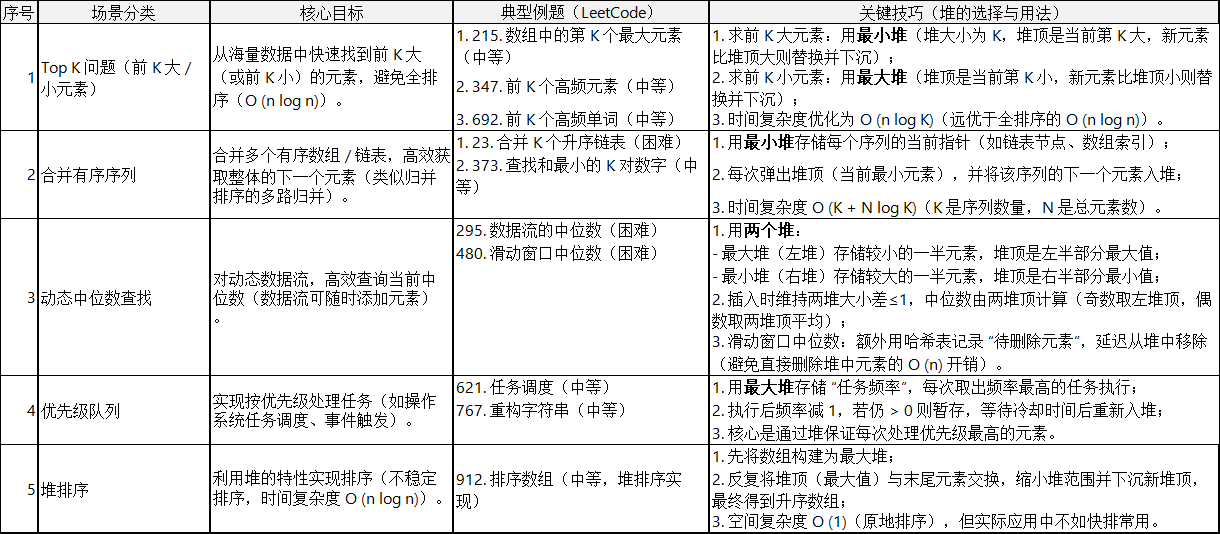
2、技巧与注意事项总结
1）堆的选择（最大堆 vs 最小堆）：
需频繁获取 “最大值”→ 最大堆（如任务调度）；
需频繁获取 “最小值”→ 最小堆（如合并 K 个有序链表）；
平衡场景（如中位数）→ 大小堆结合。
2）处理 “动态删除非堆顶元素”：
堆不支持高效删除任意元素（需 O (n) 查找），实际中常用 “延迟删除” 技巧：
用哈希表记录 “待删除元素” 的次数；
当堆顶元素是待删除元素时，才将其弹出并减少计数，避免提前处理。
3）堆的实现方式：
语言内置结构：C++ 的priority_queue（默认最大堆，最小堆需用greater<>）、Python 的heapq（默认最小堆，最大堆需取负）；
自定义堆：通过数组 + 上浮 / 下沉函数实现，适合特殊场景（如带索引的堆）。
4）与其他数据结构的对比：
堆 vs 二叉搜索树（BST）：堆获取极值 O (1)，但不支持范围查询；BST 支持范围查询，但获取极值 O (log n)；
堆 vs 哈希表：堆适合有序场景（如 Top K），哈希表适合快速查找但无序。

三、典型题目

215. 数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
示例 :输入: [3,2,1,5,6,4] 和 k = 2；输出: 5

    int findKthLargest(vector<int>& nums, int k) {priority_queue<int,vector<int>,greater<int>> small_heap;for(auto num:nums){if(small_heap.size() < k) {small_heap.push(num);            } else {if (num > small_heap.top()) {small_heap.pop();small_heap.push(num);}}}return small_heap.top();}

347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

public:static bool cmp(pair<int, int>& m, pair<int, int>& n) {return m.second > n.second;}vector<int> topKFrequent(vector<int>& nums, int k) {// 思路：hash统计频次，然后用堆得到频次最高的K个// 1、hash统计频次, key为num值，value为次数unordered_map<int, int> freqhash;for (auto &num : nums) {freqhash[num]++;}//２、构建小顶堆 维持总数为K个, 元素1为值，元素2为次数priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(&cmp)> freqheap(cmp);for (auto &[num, count] : freqhash) {if (freqheap.size() == k) {if (freqheap.top().second < count) {freqheap.pop();freqheap.emplace(num, count);}} else {freqheap.emplace(num, count);}}// 3、构建结果vector <int> result;while (!freqheap.empty()) {result.emplace_back(freqheap.top().first);freqheap.pop();}return result;}

373. 查找和最小的 K 对数字
给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。

class Solution {
public:vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {// 思路：初始筛选出 “最可能是小和” 的候选数对，用最小堆动态维护这些候选// 简化技巧，利用数组 “越往后越大” 的特性，先抓最可能小的组合// 每次选完最小的，只扩展它的 “下一个可能”，既高效又不遗漏。// 最小堆的比较器,auto cmp = [&nums1, &nums2](const pair<int, int> & a, const pair<int, int> & b) {return nums1[a.first] + nums2[a.second] > nums1[b.first] + nums2[b.second];};int m = nums1.size();int n = nums2.size();vector<vector<int>> ans;// 最小堆：存储索引对(i,j)，按数对和从小到大排序priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);for (int i = 0; i < min(k, m); i++) {pq.emplace(i, 0); // (nums1[i], nums2[0])是nums1[i]能形成的最小和数对}while (k-- > 0 && !pq.empty()) {// 每次从堆顶取出和最小的数对索引(x, y)auto [x, y] = pq.top(); pq.pop();ans.emplace_back(initializer_list<int>{nums1[x], nums2[y]});// 补充新候选：当前数对是(x,y)，下一个可能的候选是(x, y+1)// 无需补充(x+1, y)，因为(x+1, 0)已在初始化时加入堆中，后续会逐步处理y递增的情况if (y + 1 < n) {pq.emplace(x, y + 1);}}return ans;}

295. 数据流的中位数
中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。
例如，[2,3,4] 的中位数是 3；[2,3] 的中位数是 (2 + 3) / 2 = 2.5；设计一个支持以下两种操作的数据结构：void addNum(int num) - 从数据流中添加一个整数到数据结构中。double findMedian() - 返回目前所有元素的中位数。

     /* 大顶堆 放小的一半，堆顶为最大值 */priority_queue<int, vector<int>, less<int>> low_heap;/* 小顶堆 放大的一半，堆顶为最小值 */priority_queue<int, vector<int>, greater<int>> high_heap;
public:// Adds a number into the data structure.void addNum(int num){if (low_heap.empty() == true) {low_heap.push(num);return;}if (low_heap.size() == high_heap.size()) {/* 两堆数量一样多，按实际大小判断放哪一堆里面 */if (num > low_heap.top()) {high_heap.push(num);} else {low_heap.push(num);               }} else if (high_heap.size() > low_heap.size()) {/* 大的数比较多，优先放low堆，放不进去就把high的top换过来 */if (num <= high_heap.top()) {low_heap.push(num);} else {low_heap.push(high_heap.top());high_heap.pop();high_heap.push(num);}} else {/* 小的数比较多，优先放high堆，放不进去就把low的top换过来 */if (num >= low_heap.top()) {high_heap.push(num);} else {high_heap.push(low_heap.top());low_heap.pop();low_heap.push(num);}}}double findMedian(){if (low_heap.size() == high_heap.size()) {return (low_heap.top() + high_heap.top()) / 2.0;} else if (low_heap.size() > high_heap.size()) {return low_heap.top();} else {return high_heap.top();}}

767. 重构字符串
给定一个字符串 s ，检查是否能重新排布其中的字母，使得两相邻的字符不同。返回 s 的任意可能的重新排列。若不可行，返回空字符串 “” 。

class Solution {
public:string reorganizeString(string s) {// 思路：贪心+最大堆// 如果某个字符出现次数过多（超过 (总长度+1)/2），则必然无法避免相邻重复// 如何获得字串，利用优先队列（最大堆）每次取出出现次数最多的两个字符，交替放置（避免相邻重复）// 减少计数后将剩余次数的字符重新入队，直到所有字符排列完成。if (s.length() < 2) {return s;}vector<int> counts(26, 0);int maxCount = 0;int length = s.length();// 可行性判断：若最大次数超过 (length+1)/2，必然有相邻重复for (int i = 0; i < length; i++) {char c = s[i];counts[c - 'a']++;maxCount = max(maxCount, counts[c - 'a']);}if (maxCount > (length + 1) / 2) {return "";}// 定义比较器：按字符出现次数降序排列（次数多的优先级高）auto cmp = [&](const char& letter1, const char& letter2) {return counts[letter1 - 'a']  < counts[letter2 - 'a'];};// 优先队列（最大堆）：存储字符，按上述比较器排序priority_queue<char, vector<char>,  decltype(cmp)> queue{cmp};for (char c = 'a'; c <= 'z'; c++) {if (counts[c - 'a'] > 0) {queue.push(c);}}string sb = "";while (queue.size() > 1) {// 每次取两个不同的字符排列（避免相邻重复）char letter1 = queue.top(); queue.pop();char letter2 = queue.top(); queue.pop();sb += letter1;sb += letter2;int index1 = letter1 - 'a', index2 = letter2 - 'a';// 减少计数后，若仍有剩余，重新入队counts[index1]--;counts[index2]--;if (counts[index1] > 0) {queue.push(letter1);}if (counts[index2] > 0) {queue.push(letter2);}}// 若队列中剩余1个字符（字符串长度为奇数时），直接拼接（此时它的计数为1，且前一个字符与它不同）if (queue.size() > 0) {sb += queue.top();}return sb;}
};

912. 排序数组
给你一个整数数组 nums，请你将该数组升序排列。你必须在 不使用任何内置函数 的情况下解决问题，时间复杂度为 O(nlog(n))，并且空间复杂度尽可能小。

class Solution {// 调整堆：确保以i为根的子树满足最大堆性质void maxHeapify(vector<int>& nums, int i, int len) {for (; (i << 1) + 1 <= len;) {int lson = (i << 1) + 1;  // 左孩子索引：2*i + 1int rson = (i << 1) + 2;  // 右孩子索引：2*i + 2int large;                // 记录当前节点、左孩子、右孩子中最大值的索引if (lson <= len && nums[lson] > nums[i]) {large = lson;} else {large = i;}if (rson <= len && nums[rson] > nums[large]) {large = rson;}// 如果最大值不是当前节点，需要交换并继续下沉if (large != i) {swap(nums[i], nums[large]);i = large;} else {break;}}}// 构建最大堆，将无序数组转换为最大堆。void buildMaxHeap(vector<int>& nums, int len) {// 从最后一个非叶子节点开始，向前遍历并调整每个节for (int i = len / 2; i >= 0; --i) {maxHeapify(nums, i, len);}}void heapSort(vector<int>& nums) {int len = (int)nums.size() - 1;buildMaxHeap(nums, len);         // 第一步：构建最大堆for (int i = len; i >= 1; --i) {swap(nums[i], nums[0]);      // 交换堆顶（最大值）和当前堆尾（i位置），最大值归位len -= 1;                    // 堆的范围缩小（排除已归位的最大值）maxHeapify(nums, 0, len);    // 调整新堆顶，恢复最大堆性质}}
public:vector<int> sortArray(vector<int>& nums) {heapSort(nums);return nums;}
};