2024年ASOC SCI2区TOP，费马-韦伯定位粒子群算法+无人机协同路径规划，深度解析+性能实测

---

1.摘要

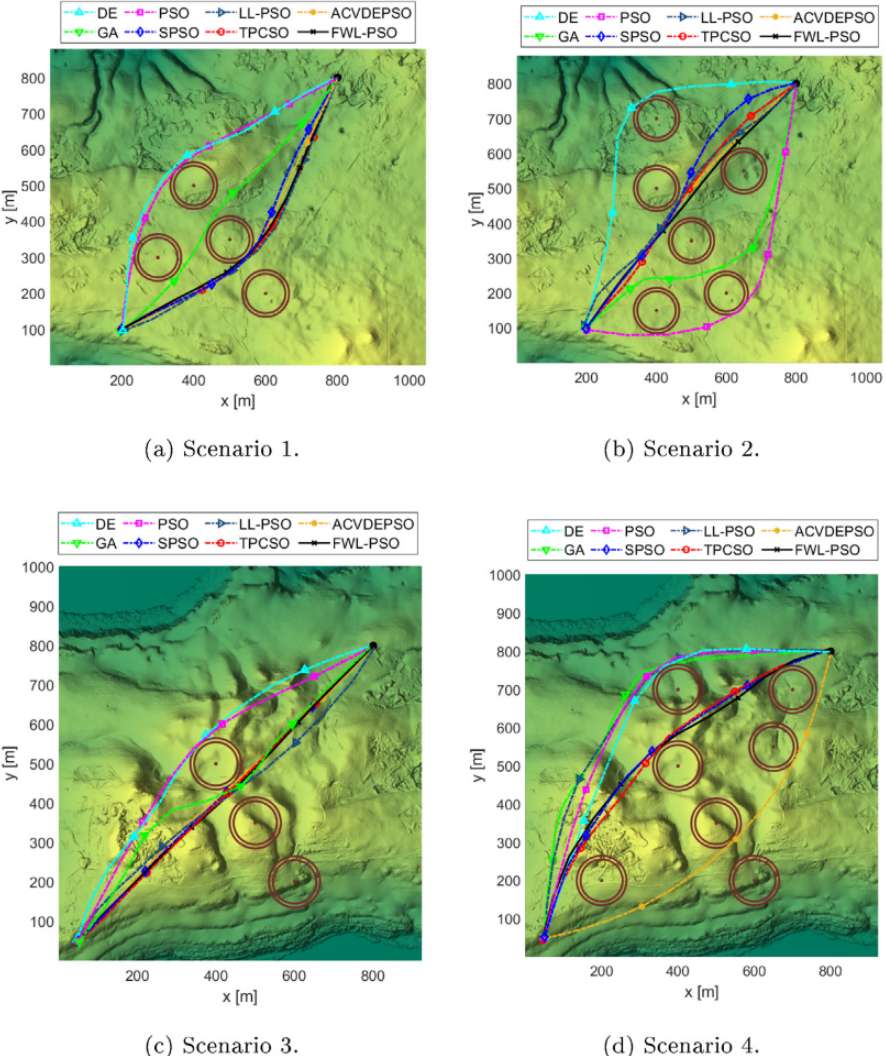
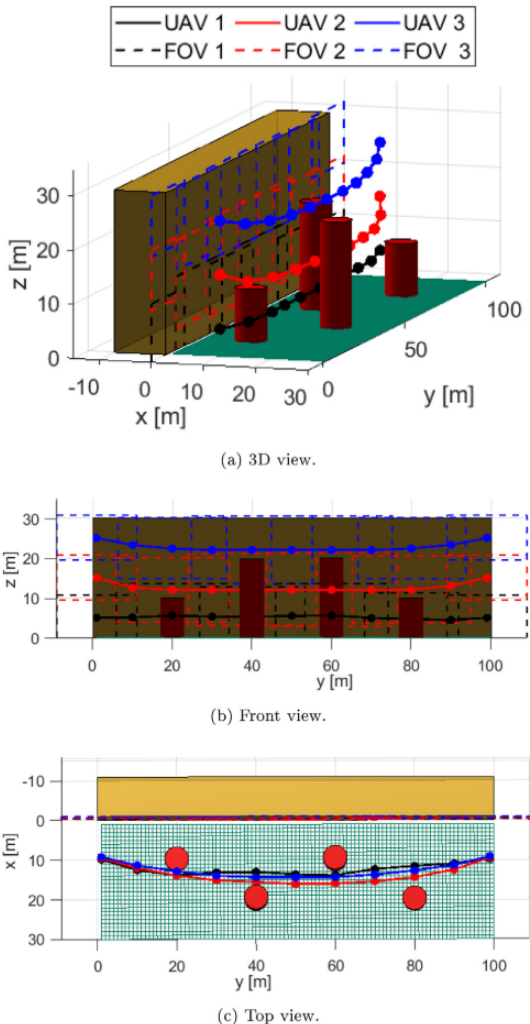
本文提出了一种基于费马-韦伯定位粒子群算法（FWL-PSO），FWL-PSO通过引入费马-韦伯最优点来识别潜在解空间，并在算法框架内构建由适应度评分筛选的优质粒子集合。通过计算精英粒子的费马-韦伯定位点替代传统全局最优解，有效增强了标准粒子群算法的学习机制，在促进搜索多样性的同时实现信息协同进化。在多无人机协同应用方面，本文将集群路径规划建模为包含协同约束与安全条件的纳什博弈问题，并采用FWL-PSO算法求解该优化问题的纳什均衡解。

2.费马-韦伯定位粒子群算法

给定${\mathbb{R}}^n$空间中的$p$个顶点$X_1,X_2,\dots ,X_p$及与之关联的权重${\eta }_i>0$ ($i=1,\dots ,p$)，费马-韦伯定位点（几何中位数），被定义为最小化从任意点$Y\in {\mathbb{R}}^n$ 到各顶点$X_i$ 的加权距离和的点：
$$\hat{Y}=\underset{Y\in {\mathbb{R}}^n}{\mathrm{argmin}}\left\{f(Y)=\sum _{i=1}^p{\eta }_i\Vert X_i-Y{\Vert }_2\right\}$$

公式采用欧几里得范数，在费马-韦伯定位点满足：
$$\nabla f(\hat{Y})=\sum _{i=1}^p\frac{{\eta }_i(X_i-\hat{Y})}{\Vert X_i-\hat{Y}{\Vert }_2}=0$$

由于没有显示解，采用Weiszfeld迭代算法，通过不断计算加权平均点来逐步逼近该几何中位数。

FWL-PSO 算法在初始化后，会筛选出表现最优的约5%粒子组成精英池，并将其中排名第一的粒子直接设为全局最优解。FWL-PSO算法会计算这些精英粒子的费马-韦伯定位点——这个几何中心点是使其与各精英粒子之间总距离最小的点，有效地概括了它们的空间分布。它作为精英粒子集体影响的参考点，将群体引导向更具潜力的区域，其定义为：
$$\hat{F}=\underset{F\in {\mathbb{R}}^D}{\mathrm{argmin}}\sum _{i=1}^p{\eta }_i\Vert X_p^e(i,;)-F{\Vert }_2$$

粒子速度更新：
$$V(t+1)=c_0\times V(t)+c_1\times R_1\circ (X_P(t)-X(t))+c_2\times R_2\circ (1_N\times F(t)-X(t))$$

3.结果展示

4.参考文献

[1] Van Nguyen L, Kwok N M, Ha Q P. Fermat-Weber location particle swarm optimization for cooperative path planning of unmanned aerial vehicles[J]. Applied Soft Computing, 2024, 167: 112269.

5.代码获取

xx

6.算法辅导·应用定制·读者交流

xx