MATLAB构造10 阶幻方（Strachey 方法）

1.Strachey 方法

Strachey 方法（斯特雷奇法）的原理，它是构造偶数阶幻方的一种经典方法，尤其适用于n ≡ 2 (mod 4) 的情况（也就是 n = 2, 6, 10, 14, …）。

2.MATLAB代码

function main()
clc;close all;clear all;warning off;%清除变量
rand('seed', 100);
randn('seed', 100);
format long g;n = 10;
if mod(n, 4) ~= 2error('本算法只适用于 n ≡ 2 (mod 4) 的情况，例如 2, 6, 10, 14...');
endm = n / 2;
M = zeros(n);% 步骤1：构造左上 A 和右下 D
A = siamese(m);
D = siamese(m);% 步骤2：构造右上 B 和左下 C
B = siamese(m);
C = siamese(m);% 步骤3：填充大矩阵
M(1:m, 1:m) = A;
M(1:m, m+1:n) = B;
M(m+1:n, 1:m) = C;
M(m+1:n, m+1:n) = D;% 步骤4：交换中间部分元素
k = (m - 1) / 2; % 对于 m=5, k=2
% 交换 A 和 C 的中间 k×k
temp = M(1:k, 1:k);
M(1:k, 1:k) = M(m+1:m+k, 1:k);
M(m+1:m+k, 1:k) = temp;% 交换 B 和 D 的中间 k×(m-1)
temp = M(1:k, m-k+2:m);
M(1:k, m-k+2:m) = M(m+1:m+k, m-k+2:m);
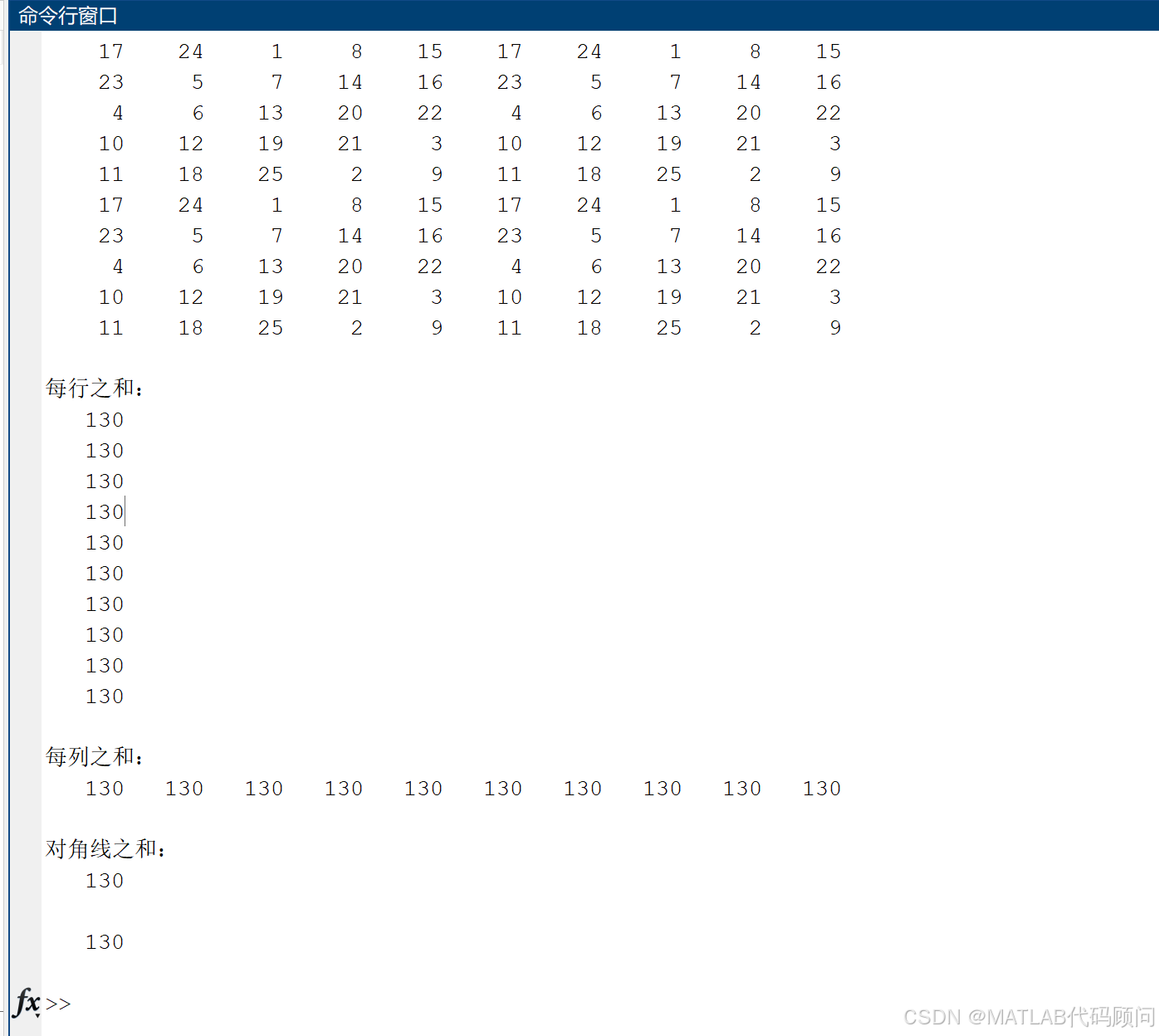
M(m+1:m+k, m-k+2:m) = temp;disp(M);
disp('每行之和：');
disp(sum(M, 2));
disp('每列之和：');
disp(sum(M, 1));
disp('对角线之和：');
disp(sum(diag(M)));
disp(sum(diag(flipud(M))));endfunction S = siamese(m)
% 生成 m×m 的暹罗法幻方（适用于奇数阶）
S = zeros(m);
i = 1;
j = (m + 1) / 2;
for num = 1:m^2S(i, j) = num;% 上移右移ni = i - 1;nj = j + 1;if ni < 1ni = m;endif nj > mnj = 1;endif S(ni, nj) == 0i = ni;j = nj;else% 冲突则下移i = i + 1;if i > mi = 1;endend
end
end

3.程序结果