[优选算法专题三.二分查找——NO.23搜索旋转排序数组中的最⼩值]

题目链接

153. 寻找旋转排序数组中的最小值

题目描述

题目解答

• 时间复杂度：代码使用了二分查找算法，每次循环都会将搜索范围缩小一半，因此时间复杂度为 O (log n)，其中 n 是数组 nums 的长度。
• 空间复杂度：代码中只使用了 left、right、mid 和 x 等几个常量级别的变量，没有使用额外的与数组长度相关的空间，所以空间复杂度为 O (1)。

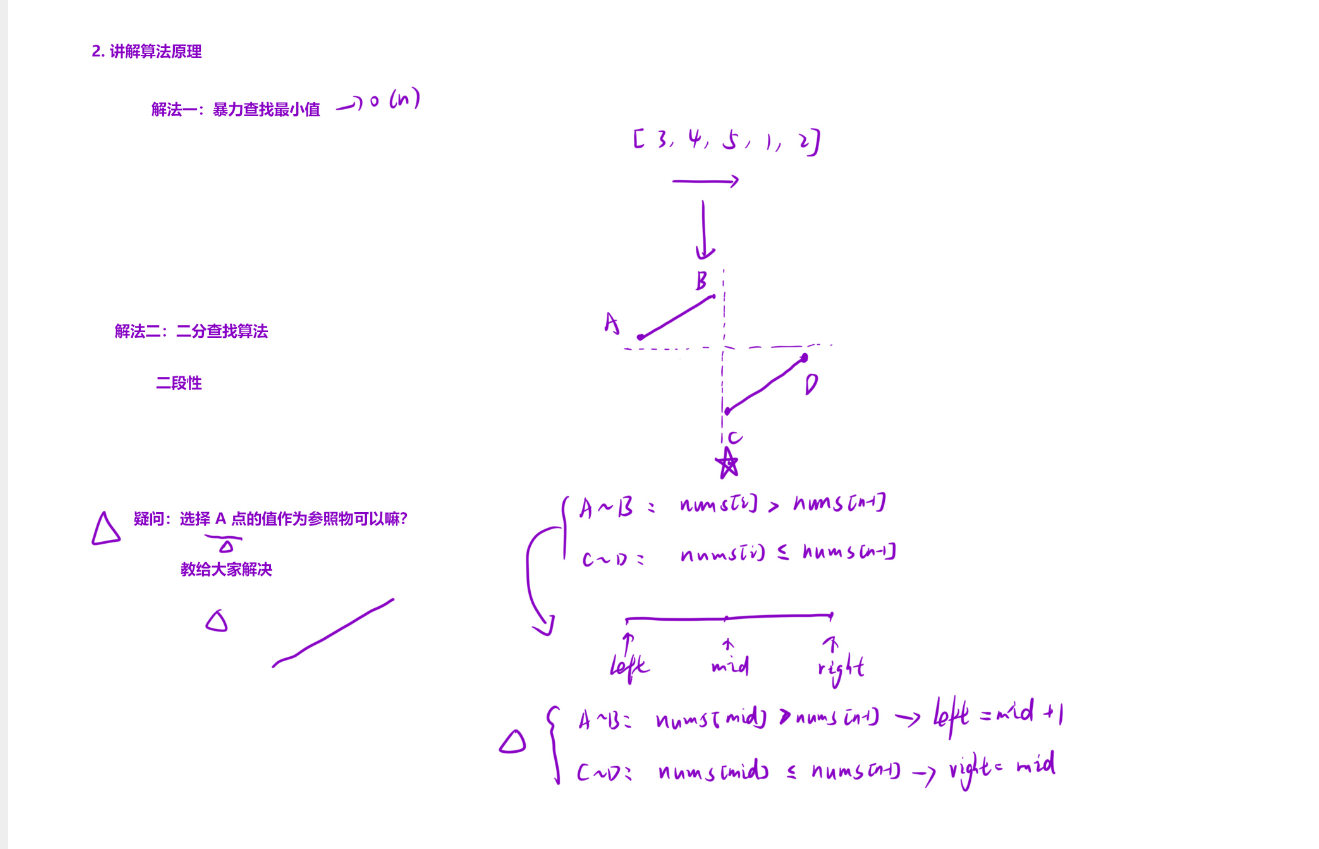
• 功能：输入一个原本升序，在某个位置旋转后得到的整数数组nums，通过二分查找算法，返回数组中的最小值。
• 代码逻辑：
  • 初始化：int left = 0, right = nums.size() - 1;定义了左右指针，分别指向数组的起始和末尾位置。int x = nums[right];获取数组的最后一个元素，用于后续比较。
  • 二分查找循环：while (left < right)确保查找区间内至少有两个元素。循环内通过int mid = left + (right - left) / 2;计算中间位置，避免了left + right可能产生的整数溢出问题。
  • 判断与更新区间：如果nums[mid] > x，说明最小值在mid的右侧，因此将左指针left更新为mid + 1；否则，说明最小值在mid及其左侧，将右指针right更新为mid。
  • 返回结果：当循环结束时，left和right会指向同一个位置，该位置即为最小值所在的位置，所以返回nums[left]。

例如，对于数组[4, 5, 6, 7, 0, 1, 2]，第一次二分mid指向6，nums[mid]>x成立，left更新为mid+1即4；第二次二分mid指向0，nums[mid]>x不成立，right更新为mid即4；此时left和right相等，循环结束，返回nums[left]，也就是0，成功找到最小值。