深度学习（十二）：多种激活函数

在深度学习模型中，激活函数（Activation Function）扮演着至关重要的角色。它决定了神经网络的非线性建模能力。若无激活函数，深层神经网络仅能退化为线性变换的堆叠，即使网络再深，最终也只能表示线性映射，无法有效地拟合复杂的非线性问题。因此，激活函数不仅是神经网络区别于传统线性模型的关键，而且直接影响训练的收敛速度、梯度传播情况以及模型的最终性能。

常见激活函数

Sigmoid 函数

定义：

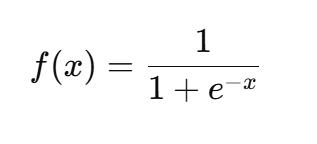
特点：

• 输出范围在 (0,1)，可看作概率。
• 在 0 附近较为敏感，两端趋于饱和。

优点：

• 直观，输出值稳定在区间内。
• 适合二分类任务的最后一层。

缺点：

• 容易出现梯度消失问题，大的正负输入梯度接近 0。
• 非零均值，可能导致训练收敛慢。

应用：早期神经网络（如BP网络）、逻辑回归输出层。

Tanh 函数

定义：

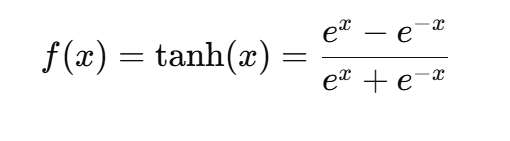
特点：

• 输出范围 (-1,1)，零均值。

优点：

• 相比 Sigmoid，数据分布更居中，收敛更快。
• 对负输入也有激活效果。

缺点：

• 同样存在梯度消失问题。
• 饱和区会使参数更新停滞。

应用：RNN 等循环神经网络中常用。

ReLU 函数

定义：

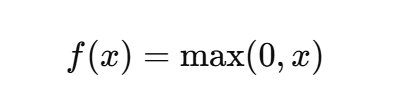
特点：

• 简单高效，非线性显著。

优点：

• 计算简单，加速训练收敛。
• 避免梯度消失（正区间梯度恒为1）。

缺点：

• “神经元死亡”问题：若长期输入为负，梯度为 0，权重无法更新。
• 输出非零均值。

应用：CNN、MLP 中最常用的激活函数。

Leaky ReLU

定义：

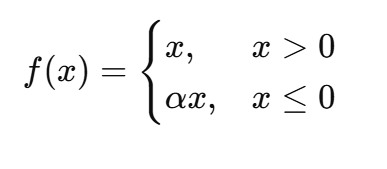
其中 α 是一个小常数（如0.01）。

优点：

• 缓解了 ReLU 神经元死亡问题。
• 保留了负区间的微弱梯度。

缺点：

• 超参数 α 需要手动设定。

应用：目标检测、图像分类等深度 CNN 模型。

Parametric ReLU (PReLU)

定义：与 Leaky ReLU 类似，但 α\alphaα 作为可学习参数。

优点：

• 自适应地调整负区间斜率。
• 在某些图像识别任务中能提升精度。

缺点：

• 增加了参数量，可能过拟合。

Exponential Linear Unit (ELU)

定义：

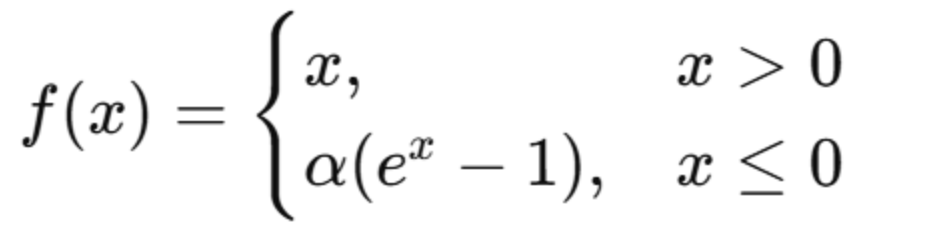
优点：

• 输出均值更接近零。
• 负区间平滑，有助于梯度流动。

缺点：

• 计算比 ReLU 更复杂。
• α 超参数需调节。

Swish

定义：

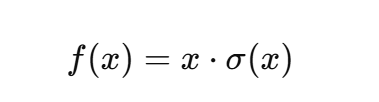
特点：由 Google 提出，兼具平滑性与非线性。

优点：

• 无硬拐点，梯度流动更稳定。
• 在深层模型中往往优于 ReLU。

缺点：

• 计算开销稍大。

应用：BERT、EfficientNet 等大型模型。

Gaussian Error Linear Unit (GELU)

定义：

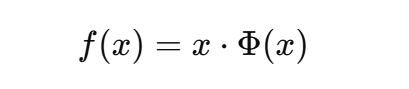
其中 Φ(x) 是标准正态分布的累积分布函数。

特点：

• 与 Swish 类似，但来源于概率建模。
• 近似形式为：

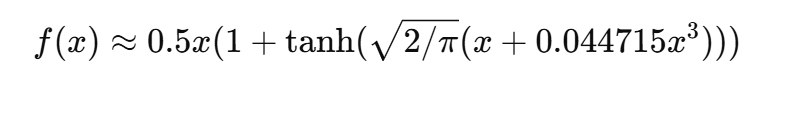
优点：

• 在 Transformer 等模型中效果优异。
• 平滑且自带概率特性。

缺点：

• 计算比 ReLU 复杂。

应用：GPT、BERT、Vision Transformer 等现代大模型。

Softmax

定义：

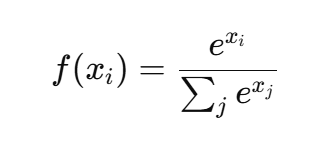
特点：

• 将向量映射为概率分布。

优点：

• 多分类任务输出必不可少。
• 与交叉熵损失结合自然。

缺点：

• 容易数值溢出，需要做数值稳定处理。
• 不适合作为隐藏层激活。

激活函数比较

函数	输出范围	是否零均值	梯度消失	主要问题	典型应用
Sigmoid	(0,1)	否	是	饱和、梯度消失	二分类输出层
Tanh	(-1,1)	是	是	饱和	RNN
ReLU	[0,∞)	否	否	神经元死亡	CNN/MLP
Leaky ReLU	(-∞,∞)	否	较少	超参数	改进 CNN
PReLU	(-∞,∞)	否	较少	过拟合风险	图像识别
ELU	(-α,∞)	近似是	较少	计算复杂	深层网络
Swish	(-∞,∞)	近似是	否	计算复杂	NLP/CNN
GELU	(-∞,∞)	近似是	否	计算复杂	Transformer
Softmax	(0,1)	否	-	数值稳定性	分类输出层

总结

激活函数是深度学习网络的“非线性引擎”。从 Sigmoid 到 ReLU，再到 Swish 与 GELU，激活函数的演化体现了深度学习对梯度消失、收敛速度和表达能力的持续优化。当前主流模型多采用 ReLU 及其改进型，而在自然语言处理和计算机视觉的前沿任务中，Swish 与 GELU 已逐渐成为标配。