机器学习——线性回归详解

一、线性回归定义

房子价格根据房子面积、房子位置、房子楼层、房子朝向四个特征来预测

1. 线性回归(Linear regression)是利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。
2. 数学公式：$h(w)=w_1{x}_1+w_2{x}_2+w_3{x}_3+...+b=w^{T}x+b$

二、损失函数

1. 误差概念：用预测值y – 真实值y就是误差

显然我们希望误差越小越好，而所有的点加起来的误差我们称之为损失函数

2. 损失函数：衡量每个样本预测值与真实值效果的函数

• 均方误差 (Mean-Square Error, MSE)：$J(w,b)=\frac{1}{m}{\sum }_{i=0}^m(h(x{)}^{(i)}-y^{(i)}{)}^2$
• 平均绝对误差 (Mean Absolute Error , MAE)：$J(w,b)=\frac{1}{m}{\sum }_{i=0}^m|h(x{)}^{(i)}-y^{(i)})|$

显然这是一个二元二次方程组，包含w和b两个参数，当我们希望求得误差最小，即损失函数最小时，就需要求得w和b在什么情况下是的$J(w,b)$最小，那么只需要对两个变量求偏导

2.1 正规方程

事实上，我们可以将b看做$x_0$，那么$（b,x_1,x_2.,..,x_d）$可以看做$（x_0,x_1,x_2.,..,x_d）$，而$w_1{x}_1+w_2{x}_2+w_3{x}_3+....+b$可以看做$w_1{x}_1+w_2{x}_2+w_3{x}_3+...+w_0$，写矩阵即
$$\left[\begin{array}{ccccc}{x}_1& x_2& x_3& ...& 1\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\\ ...\\ w_0\end{array}\right]$$

1. 矩阵的正规方程为：
   $$J(w)=(h(x_1)-y_1{)}^2+(h(x_2)-y_2{)}^2+...+(h(x_m)-y_m{)}^2=\sum _{i=1}^m(h(x_i)-y_i{)}^2=||Xw-y|{|}_2^2$$
   求解W：
   

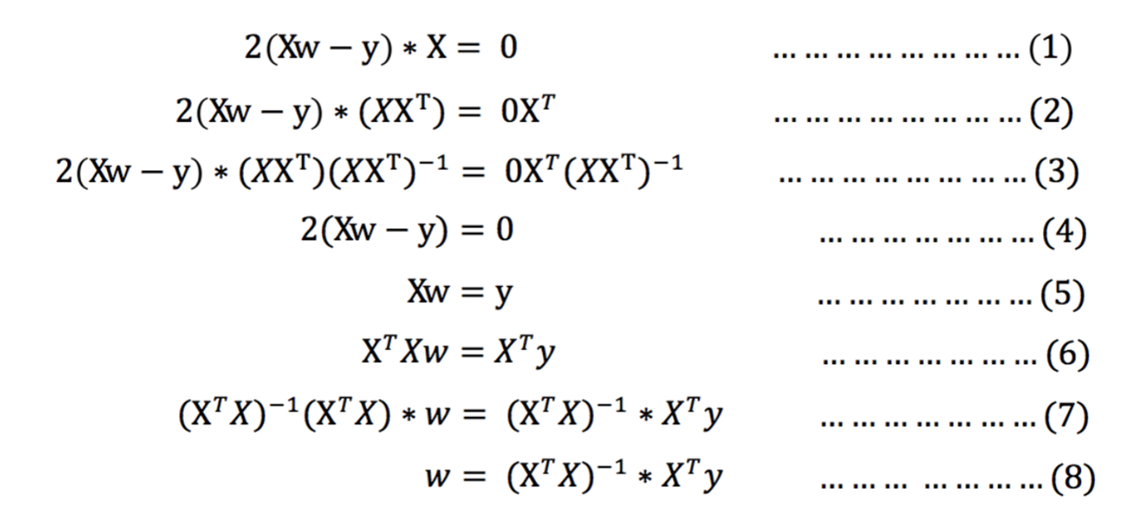
2. 正规方程的API：

from sklearn.linear_model import LinearRegression
estimator = LinearRegression(fit_intercept=True)

2.2 梯度下降

1. 梯度的定义：

• 单变量中，梯度就是某一点切线斜率（某一点的导数）；有方向为函数增长最快的方向
• 多变量函数中，梯度就是某一个点的偏导数；有方向：偏导数分量的向量方向

2. 梯度下降公式：

• 循环迭代求当前的梯度，更新当前的权重参数${\theta }_{i+1}={\theta }_i-\alpha \frac{\partial }{\partial {\theta }_i}J(\theta )$
• $\alpha$：学习率（步长），不能太大，也不能太小，机器学习中：0.001 ~ 0.01
• 梯度是上升最快的方向，我们需要的是下降最快的方向，所以需要加符号
  

事实上，在图形上看，$\alpha$就是将导数进行以其原点进行旋转，$\alpha$越大，旋转的力度越强，迈的步子就越长；$\alpha$越小，旋转的力度越弱，迈的步子就越短

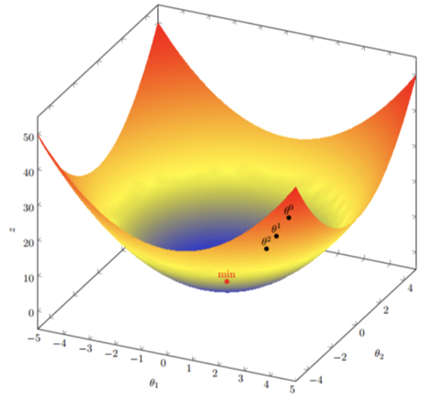
3. 对于多维梯度下降，假设函数为$J(\theta )={\theta }_1^2+{\theta }_2^2$，那么其梯度为$(2{\theta }_1,2{\theta }_2)$
   

4. 梯度下降API：

from sklearn.linear_model import SGDClassifier
estimator = SGDClassifier(learning_rate="constant", eta0=0.01)

2.3 例子

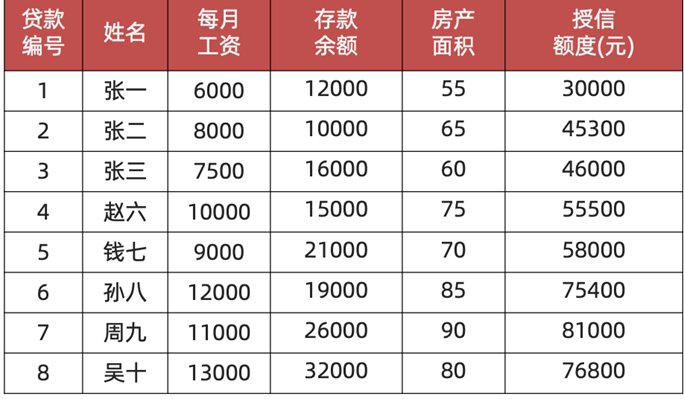
已知8个信贷人的数据，求线性回归模型

• 求线性回归模型的本质就是求各个参数对应的权重

我们已知参数的特征为每月工资、存款余额、房产面积，希望预测授信额度

1. 假设线性回归模型为：$h(\theta )={\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+{\theta }_0{x}_0$，其中$x_0$为1,
   将其化简$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
2. 带入损失函数：${\theta }_{i+1}={\theta }_i-\alpha \frac{\partial }{\partial {\theta }_i}J(\theta )$
   $$\frac{\partial \mathbf{J}(\mathbf{\theta })}{\partial \mathbf{\theta }}=\frac{\partial \frac{1}{2m}{\sum }_{i=1}^m(h_{\mathbf{\theta }}(x^{(i)})-y^{(i)}{)}^2}{\partial \mathbf{\theta }}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^{(2-1)}(h_{\mathbf{\theta }}(x^{(i)})-y^{(i)}{)}_{\mathbf{\theta }}^{\prime }=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{\theta }}(x^{(i)})-y^{(i)})\frac{\partial ({\mathbf{\theta }}_0{x}_0+{\mathbf{\theta }}_1{x}_1+{\mathbf{\theta }}_2{x}_2+{\mathbf{\theta }}_3{x}_3-...)}{\partial ({\mathbf{\theta }}_0,{\mathbf{\theta }}_1,{\mathbf{\theta }}_2,...,{\mathbf{\theta }}_d)}=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{\theta }}\left(x^{(i)}\right)-y^{(i)}){\mathrm{x}}^{\mathrm{i}}$$
3. 化简得：${\theta }_{\mathrm{j}}:={\theta }_{\mathrm{j}}-\alpha \frac{1}{m}{\sum }_{i=1}^m(\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)x_{\mathrm{j}}^{(i)})$
4. 将特征参数带入，求得${\theta }_1、{\theta }_2、{\theta }_3$等

2.4 梯度下降分类

2.4.1 全梯度下降算法 FGD

1. 每次迭代时，使用全部样本的梯度值，有m个样本，求梯度时用了所以m个样本
2. 公式：${\theta }_{i+1}={\theta }_i-\alpha {\sum }_{i=0}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)x_i^{(j)}$
3. 特点：由于使用全部数据集，训练速度较慢

2.4.2 随机梯度下降算法 SGD

1. 每次迭代时，随机选择并使用一个样本梯度值
2. 公式：${\theta }_{i+1}={\theta }_i-\alpha {\sum }_{i=0}^m(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)x_i^{(j)}$
3. 特点：简单,高效,不稳定；SG每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解

2.4.3 小批量梯度下降算法 mini-bantch

1. 每次迭代时，随机选择并使用小批量的样本梯度值，从m个样本中，选择x个样本进行迭代（1<x<m）
2. 公式：${\theta }_{i+1}={\theta }_i-\alpha {\sum }_{i=t}^{t+x-1}(h_{\theta }(x_0^{(j)},x_1^{(j)},\cdots ,x_n^{(j)})-y_j)x_i^{(j)}$
3. 若batch_size=1，则变成了SG；若batch_size=n，则变成了FGD
4. 特点：结合了SG的胆大和FG的心细，它的表现也正好居于SG和FG二者之间。目前使用最多，正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点

2.4.4 随机平均梯度下降算法 SAG

1. 每次迭代时，随机选择一个样本的梯度值和以往样本的梯度值的平均值
2. 公式：${\theta }_{i+1}={\theta }_i-\frac{\alpha }{n}{\sum }_{j=1}^n(h_{\theta }(x_0^{(j)},x_1^{(j)},\dots x_n^{(j)})-y_j)x_i^{(j)}$
3. 流程：

• 随机选择一个样本，假设选择D样本，计算其梯度值并存储到列表：[D]，然后使用列表中的梯度值均值，更新模型参数
• 随机再选择一个样本，假设选择G样本，计算其梯度值并存储到列表：[D,G],然后使用列表中的梯度值均值，更新模型参数
• 随机再选择一个样本，假设又选择了D样本，重新计算该样本梯度值，并更新列表中D样本的梯度值，使用列表中梯度值均值,更新模型参数
• 以此类推，直至收敛

4. 特点：训练初期表现不佳，优化速度较慢。这是因为我们常将初始梯度设为0，而SAG每轮梯度更新都结合了上一轮梯度值

2.5 正规方程与梯度下降的对比

	梯度下降	正规方程
学习率	需要选择学习率	不需要学习率
迭代	需要迭代求解	一次运算得出
应用场景	特征数量较大可以使用	小数据量场景、精准的数据场景
缺点	学习率未知、只能无限逼近不能求得最优解	计算量大、容易收到噪声、特征强相关性的影响
注意	梯度下降在各种损失函数求解中大量使用	$X^{T}X$的逆矩阵不存在时,无法求解
	深度学习模型参数很轻松就上亿	计算$X^{T}X$的逆矩阵非常耗时
	只能通过迭代的方式求最优解	如果数据规律不是线性的,无法使用或效果不好

三、回归评估方法

3.1 平均绝对误差 Mean Absolute Error (MAE)

1. 公式：$MAE=\frac{1}{n}{\sum }_{i=1}^n|y_i-{\hat{y}}_i|$
2. n 为样本数量，y 为实际值，MAE 越小模型预测约准确

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_predict)

3.2 均方误差 Mean Squared Error (MSE)

1. 公式：$MSE=\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2$
2. n 为样本数量，y 为实际值，MSE 越小模型预测约准确

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)

3.3 均方根误差 Root Mean Squared Error (RMSE)

1. 公式：$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}$
2. n 为样本数量，y 为实际值，RMSE 越小模型预测约准确
3. 注：由于RMSE的计算公式中有一个平方项，因此RMSE 会放大预测误差较大的样本对结果的影响，当有较大误差项，但异常点极少，可以使用MAE

4. 波士顿房价预测案例

# 0.导包
# from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error# 1.加载数据
# boston = load_boston()
# print(boston)
import pandas as pd
import numpy as npdata_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]# 2.数据集划分
# x_train,x_test,y_train,y_test =train_test_split(boston.data,boston.target,test_size=0.2,random_state=22)
x_train,x_test,y_train,y_test =train_test_split(data,target,test_size=0.2,random_state=22)# 3.标准化
process=StandardScaler()
x_train=process.fit_transform(x_train)
x_test=process.transform(x_test)# 4.模型训练
# 4.1 实例化(正规方程)
# model =LinearRegression(fit_intercept=True)
model = SGDRegressor(learning_rate='constant',eta0=0.01)
# 4.2 fit
model.fit(x_train,y_train)# print(model.coef_)
# print(model.intercept_)
# 5.预测
y_predict=model.predict(x_test)print(y_predict)# 6.模型评估print(mean_squared_error(y_test,y_predict))

5. 欠拟合和过拟合

1. 过拟合：一个假设 在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据 (体现在准确率下降)，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

2. 欠拟合：一个假设 在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据 ，此时认为这个假设出现了欠拟合的现象。(模型过于简单)
   

5.1 欠拟合

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x = np.random.uniform(-3,3,size = 100)
# 线性回归模型需要二维数组
X = x.reshape(-1,1)y = 0.5* x**2 + x+2 +np.random.normal(0,1,size = 100)from sklearn.linear_model import LinearRegression
estimator = LinearRegression()
estimator.fit(X,y)
y_predict = estimator.predict(X)plt.scatter(x,y)
plt.plot(x,y_predict,color = 'r')
plt.show()

1. 欠拟合产生原因： 学习到数据的特征过少

2. 解决办法：

• 1）添加其他特征项，有时出现欠拟合是因为特征项不够导致的，可以添加其他特征项来解决

• 2）添加多项式特征，模型过于简单时的常用套路，例如将线性模型通过添加二次项或三次项使模型泛化能力更强

5.2 过拟合

X5 = np.hstack([X,X**2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10])estimator3 = LinearRegression()
estimator3.fit(X5,y)
y_predict5 = estimator3.predict(X5)plt.scatter(x,y)
plt.plot(np.sort(x),y_predict5[np.argsort(x)],color = 'r')
plt.show()error = mean_squared_error(y, y_predict5)
error#1.0508466763764157

1. 过拟合产生原因： 原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾所有测试样本

2. 解决办法：

• 1）重新清洗数据，导致过拟合的一个原因有可能是数据不纯，如果出现了过拟合就需要重新清洗数据。

• 2）增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。

5.3 正则化

5.3.1 L1正则化

1. L1范数：$x^T=(1,2,-3)\Vert \mathrm{x}{\Vert }_1=|1|+|2|+|-3|=6$
2. L1正则化，在损失函数中添加L1正则化项：$J(w)=\mathrm{MSE}(w)+\alpha {\sum }_{i=1}^n|w_i|$
3. α叫做惩罚系数，该值越大则权重调整的幅度就越大，即：表示对特征权重惩罚力度就越大
4. L1正则化会使得权重趋向于0，甚至等于0，使得某些特征失效，达到特征筛选的目的

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
np.random.seed(666)
x = np.random.uniform(-3,3,size = 100)
# 线性回归模型需要二维数组
X = x.reshape(-1,1)y = 0.5* x**2 + x+2 +np.random.normal(0,1,size = 100)
X5 = np.hstack([X,X**2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10])estimator = Lasso(alpha = 0.1)
estimator.fit(X5,y)
y_predict = estimator.predict(X5)plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color = 'r')
plt.savefig("Lasso.png")
plt.show()

上图为未正则化，下图为L1正则化

5.3.2 L2正则化

1. L2范数：$x^T=(1,2,-3)\Vert \mathrm{x}{\Vert }_2=\sqrt[2]{1^2+2^2+(-3{)}^2}=\sqrt{12}$
2. L2正则化：在损失函数中添加L2正则化项：$J(w)=\mathrm{MSE}(w)+\alpha {\sum }_{i=1}^n{w}_i^2$
3. α叫做惩罚系数，该值越大则权重调整的幅度就越大，即：表示对特征权重惩罚力度就越大
4. L2正则化会使得权重趋向于0，一般不等于0，所以L2正则化用的比较多

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
np.random.seed(666)
x = np.random.uniform(-3,3,size = 100)
# 线性回归模型需要二维数组
X = x.reshape(-1,1)y = 0.5* x**2 + x+2 +np.random.normal(0,1,size = 100)
X5 = np.hstack([X,X**2,X**3,X**4,X**5,X**6,X**7,X**8,X**9,X**10])estimator = Ridge(alpha = 0.1)
estimator.fit(X5,y)
y_predict = estimator.predict(X5)plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color = 'r')
plt.savefig("Ridge.png")
plt.show()

上图为未正则化，下图为L2正则化