LeetCode算法日记 - Day 50: 汉诺塔、两两交换链表中的节点
目录
1. 汉诺塔
1.1 题目解析
1.2 解法
1.3 代码实现
2. 两两交换链表中的节点
2.1 题目解析
2.2 解法
2.3 代码实现
1. 汉诺塔
https://leetcode.cn/problems/hanota-lcci/
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例 1:
输入:A = [2, 1, 0], B = [], C = [] 输出:C = [2, 1, 0]
示例 2:
输入:A = [1, 0], B = [], C = [] 输出:C = [1, 0]
提示:
- A 中盘子的数目不大于 14 个。
1.1 题目解析
题目本质
把 n 个盘子从柱 A 按规则搬到柱 C,允许借助柱 B。问题的“骨架”就是一个标准分治:先处理 n−1,再处理最大盘,再处理 n−1。
常规解法
直观上想“能搬就搬”,但只许搬顶盘且小盘必须在大盘之上,贪心或简单循环很难保证全局次序与合法性。
问题分析
每次只能移动一个盘子,且必须保持合法叠放;为了把第 n 个(最大)盘从 A 挪到 C,必须先把上面的 n−1 个临时腾到 B——这天然形成递归子结构。最少移动步数满足 T(n)=2T(n−1)+1,指数级。
思路转折
采用分递归,把 “ n 个盘从 from 移到 to,借助 aux”作为基本子问题:A→B(n−1),A→C(1),B→C(n−1)。这既简单又能保证约束不被破坏。
1.2 解法
算法思想(递推原理):
-
若 n≤0:空操作(终止)
-
若 n>0:先把 n−1 个从 from→aux;再把最大盘 from→to;再把那 n−1 个从 aux→to
-
递推式:T(n)=T(n−1)+1+T(n−1)=2ⁿ−1
i)定义函数 move(from, aux, to, n) 表示按规则把 from 顶部的 n 个盘搬到 to,aux 为辅助。
ii)终止条件:n <= 0 直接返回,表示没有盘子可搬。
iii)递归一:move(from, to, aux, n-1),把上面 n−1 个先挪到辅助柱。
iv)核心一步:把当前层的“最大盘”从 from 顶部弹出并压入 to 顶部(栈顶是 List 的最后一个元素)。
v)递归二:move(aux, from, to, n-1),把暂存于辅助柱的 n−1 个盘再搬到目标柱。
易错点:
-
终止条件写错:n==1 不能空返回;要么用 n<=0 空操作,要么在 n==1 时搬一次再返回。
-
用了不可变/固定大小的列表:Arrays.asList(...)、List.of(...) 无法 remove/add,请用 new ArrayList<>(...)。
-
栈顶索引:from 顶盘是 list.size()-1,不要写成 0。
-
递归参数顺序:两次递归时辅助柱与目标柱会交换,注意顺序别写反。
-
空栈越界:若误让 n==0 继续执行 remove(size()-1) 会抛异常。
1.3 代码实现
import java.util.List;class Solution {public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {move(A, B, C, A.size()); // 把 A 的 n 个盘借助 B 移到 C(原地修改)}private void move(List<Integer> from, List<Integer> aux, List<Integer> to, int n) {if (n <= 0) return; // 终止:没有盘子可搬move(from, to, aux, n - 1); // 1) 先把 n-1 从 from -> auxmoveTop(from, to); // 2) 再把最大盘 from -> tomove(aux, from, to, n - 1); // 3) 最后把 n-1 从 aux -> to}// 栈顶移动:List 的最后一个元素为“顶盘”private void moveTop(List<Integer> from, List<Integer> to) {to.add(from.remove(from.size() - 1));}
}
复杂度分析:
-
时间复杂度:T(n)=2T(n−1)+1 → T(n)=2ⁿ−1,为 O(2ⁿ)。
-
空间复杂度:递归深度为 n,辅助调用栈 O(n);除输入三栈外,无额外结构。
2. 两两交换链表中的节点
https://leetcode.cn/problems/swap-nodes-in-pairs/
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
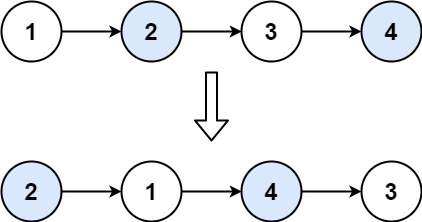
输入:head = [1,2,3,4] 输出:[2,1,4,3]
示例 2:
输入:head = [] 输出:[]
示例 3:
输入:head = [1] 输出:[1]
2.1 题目解析
题目本质
把链表按“每 2 个一组”做原地节点交换,本质是一个局部 2 节点变换 + 与后半段拼接的问题。
常规解法
最直观会想到遍历链表,把相邻两点 a,b 对调;也有人想“直接交换 val 值”。
问题分析
本题禁止改值,只能改指针;递归写法要先设计好“函数返回什么”和“基线”,很容易 NPE 或丢链。
思路转折
设计递归函数 swap(head) 的契约:返回“从 head 开始这一段两两交换后的新头”。
-
要想不丢链 → 先处理“后半段”(从第 3 个开始),拿到已交换好的新头,再把当前这对 a,b 翻转并把 a.next 接到“后半段新头”。
-
基线:head == null || head.next == null,分别兜住偶数结尾传入 null与奇数结尾单节点两种情况。
2.2 解法
算法思想(递推原理):
-
步长 = 2:递归调用 swap(head.next.next),获得“后半段交换后的新头”。
-
当前层把 a=head、b=head.next 交换成 b→a,让 a.next 指向“后半段新头”。
-
返回 b 作为这一段的新头。
-
基线:head == null || head.next == null 直接返回 head(空/单节点无需交换)。
i)若 head == null 或 head.next == null,返回 head。
ii)递归处理从第 3 个节点起的子链:tmp = swap(head.next.next),tmp 是“后半段交换后的新头”。
iii)设 cur = head.next,将当前一对翻转:先 cur.next = head(或写成 head.next.next = head)。
iv)把 head.next 指向 tmp,与后半段拼接。
v)返回 cur 作为这一段的新头。
易错点:
-
少写基线的任一条件都会出错:只判 head.next==null 会在偶数长度时递归到 null 触发 NPE;只判 head==null 会在奇数长度的尾部留下单节点未处理。
-
把 head.next 接回去时应当接递归返回的 tmp,而不是接 cur.next(注意顺序变化后 cur.next 的含义已变)。
-
修改指针次序要一致:先确定后半段、再翻当前一对、最后拼接,避免成环或断链。
2.3 代码实现
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {return swap(head);}private ListNode swap(ListNode head){// 基线:空链或单节点,原样返回(同时兜住奇偶两种结尾)if (head == null || head.next == null) return head;// 先处理后半段(从第 3 个开始),拿到已交换好的新头ListNode tmp = swap(head.next.next);// 当前一对:a=head, b=head.nextListNode cur = head.next; // bhead.next.next = head; // b -> a(翻转当前一对)head.next = tmp; // a -> 后半段新头return cur; // 返回当前段的新头(b)}
}
复杂度分析:
-
时间度分析:O(n),每个节点访问常数次。
-
空间度分析:O(n)(递归栈深 ~ n/2 层,量级 O(n))。
