力扣每日一刷Day24
Practice Day twenty-four:Leetcode T204

今天来一些数论基础吧。
先看一眼题目吧,乍一看超级简单吧,题目描述就一句话,很明了了,甚至不需要拆解。
好吧——好吧,是的,可视化还是交给我吧,我已经做了好多期的可视化了,没办法,网上没别的资源了。按照惯例,我会把他放到文章最后面。
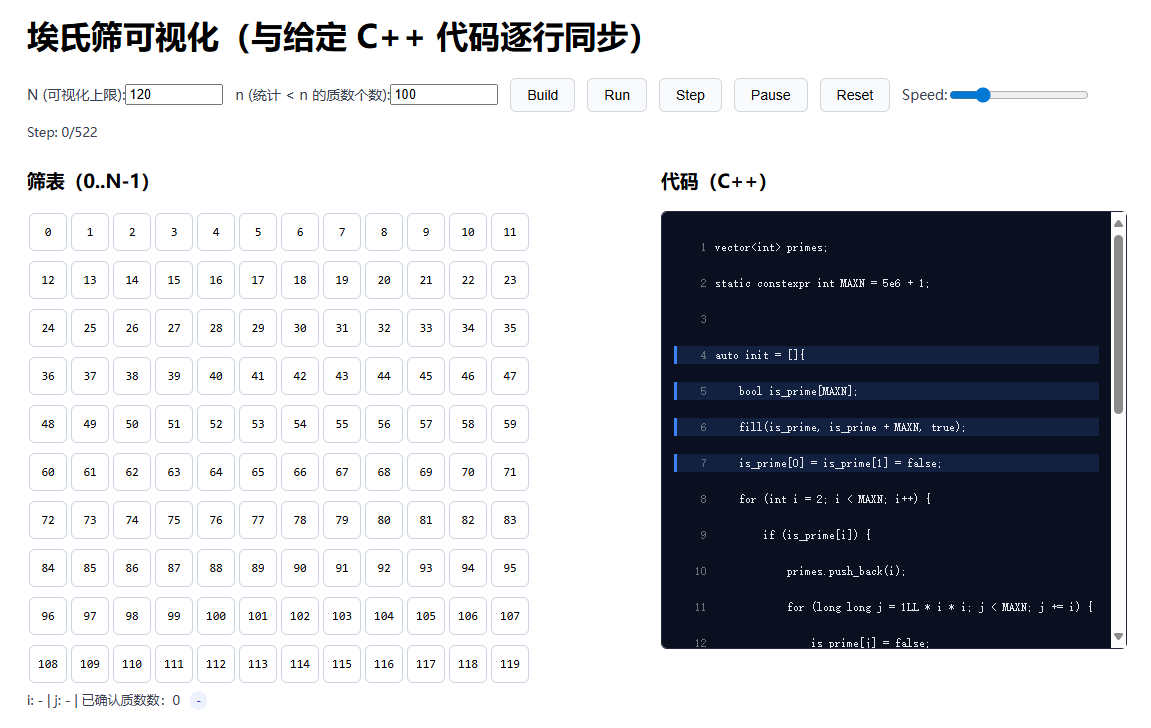
来吧,直接看代码吧。这里我先讲讲这份代码是怎么做到查找质数个数的吧。
代码使用的是 埃拉托斯特尼筛法(Sieve of Eratosthenes) 预处理素数列表,并结合 二分查找(Binary Search) 快速统计小于 n 的素数数量。
二分查找指的是我们直接把除了2以外的偶数全部杀掉了,因为我们知道偶数除2以外不会是质数。
我认为补充一些数学知识也是必要的
质数(Prime Number)是指大于 1 的自然数,且仅能被 1 和自身整除的数。换句话说,若一个数 n>1,且没有除了 1 和 n 之外的因数,则 n 是质数。
听起来不赖,再看看什么是埃拉托斯特尼筛法(Sieve of Eratosthenes)
核心逻辑
- 假设所有数都是质数,然后通过标记排除非质数。
- 从最小的质数 2 开始,将它的所有倍数(如 4, 6, 8...)标记为合数。
- 重复这个过程,对下一个未被标记的数(即质数)进行倍数标记。
- 最终未被标记的数就是质数。
好了,我们直接来代码实现吧
1 首先来些准备工作
vector<int> primes;
static constexpr int MAXN = 5e6 + 1;
vector<int> primes;
表示定义了一个名为primes的 动态数组(vector),其中每个元素是 整数类型(int)。- 用途:这个
primes数组用于保存通过筛法(如埃拉托斯特尼筛法)找到的所有质数。
对于定义的MAXN而言,这是我们定义的最大搜索范围,因为题目规定最大范围为5e6,我们设MAXN为5e6+1,加1总是可以避免很多麻烦
static:表示这个变量是静态的,在程序启动时就分配内存,并且在整个程序生命周期内有效。constexpr:表示这是一个编译时常量,可以在编译时被计算和优化。int MAXN = 5e6 + 1;:定义了一个整数常量MAXN,其值为5,000,001(即 5e6 + 1)。
2 下面,我们来实现埃拉托斯特尼筛法(Sieve of Eratosthenes)
为了逻辑的连贯,我先放出完整代码,再逐步讲解
auto init = []
{bool is_prime[MAXN];fill(is_prime, is_prime + MAXN, true);is_prime[0] = is_prime[1] = false;for (int i = 2; i < MAXN; i++){if (is_prime[i]){primes.push_back(i);for (long long j = 1LL * i * i; j < MAXN; j += i){is_prime[j] = false;}}}return 0;
}();显而易见的是,在这里,我们使用了lambda表达式,主要原因是为了在程序启动时自动执行初始化代码,并且避免污染全局命名空间或避免定义额外的函数。
bool is_prime[MAXN];- 定义一个长度为
MAXN的布尔数组is_prime。 - 每个元素的初始值为
false(未显式赋值时)。 - 这个数组用来表示从
0到MAXN - 1的所有数是否为质数。
这里我先解释一下fill函数的原型,虽然之前的讲解有描述过fill函数,但我还是希望可以再巩固一遍
template< class ForwardIt, class T >
void fill( ForwardIt first, ForwardIt last, const T& value );
ForwardIt: 一个前向迭代器类型(例如vector<int>::iterator)。first: 要填充的范围的起始迭代器。last: 要填充的范围的结束迭代器。value: 要赋给范围内每个元素的值。
fill(is_prime, is_prime + MAXN, true);- 使用
std::fill函数将is_prime数组的所有元素初始化为true。 - 表示:假设所有数都是质数(这是筛法的第一步)。
is_prime[0] = is_prime[1] = false;- 明确将
0和1标记为非质数。 - 因为根据定义,0 和 1 不是质数。
好了,完成这些必要的准备工作后,我们来进入正式的处理阶段,筛选出所有小于所给数字的素数
for (int i = 2; i < MAXN; i++){if (is_prime[i]){primes.push_back(i);for (long long j = 1LL * i * i; j < MAXN; j += i){is_prime[j] = false;}}}好了,我们来看一些新奇的东西,就比如说,这个1LL。
1LL 是 C++ 中的类型转换写法,用于表示一个 长整型(long long)类型的字面量。
现在我们知道1LL和1的数值是相同的,那么,1LL*i*i和1*i*i有什么不同呢?
1LL * i * i 和 1 * i * i 的区别在于数据类型,这会导致计算结果和行为完全不同,尤其是在处理大数时。
1LL是long long类型。i是int,但long long会自动将i提升为long long。- 所以整个表达式是
long long * long long * long long = long long,不会溢出。
| 表达式 | 数据类型 | 是否溢出? | 举例说明 |
|---|---|---|---|
1 * i * i | int(默认) | 可能溢出 | 当 i > 46340 时,i*i 超过 int 范围 |
1LL * i * i | long long | 不溢出 | 适用于更大的数值范围 |
你可能会疑惑:
“
j是long long类型了,为什么还要写1LL * i * i?”
核心原因:运算类型决定结果
在 C++ 中,表达式的类型由参与运算的变量类型决定,而不是最终赋值给哪个变量。
关键点:
- 表达式
i * i的类型是int(因为i是int)。 - 即使后面把结果赋值给
long long j,如果i * i已经溢出,那结果已经是错误的了!
哈哈,很有意思吧,我也是第一次见噢
接下来,我们以表格的形式分类代码的效用
| 代码 | 说明 |
|---|---|
for (int i = 2; i < MAXN; i++) | 遍历从 2 到 MAXN - 1 的所有整数。 |
if (is_prime[i]) | 如果当前数 i 没有被标记为非质数(即 is_prime[i] == true),说明它是质数。 |
primes.push_back(i); | 将这个质数 i 加入全局的 primes 列表中。 |
for (long long j = 1LL * i * i; j < MAXN; j += i) | 从 i*i 开始,将 i 的所有倍数(即 i*2, i*3, ...)标记为非质数。 |
is_prime[j] = false; | 标记 j 为非质数(即不是质数)。 |
你可能只是一眼扫去觉得合理,觉得也没必要深究,但是:为什么循环是从2开始,而不是什么其他别的数字?
在埃拉托斯特尼筛法中,从 2 开始是必须的,因为:
2是最小的质数。- 所有偶数(除了
2)都是合数,所以必须从2开始标记所有偶数为非质数。 - 如果从
4或更大的数开始,就会漏掉所有比它小的质数。
所以说素数的定义真是很美好啊,他没有让2之前的数字0,1也成为质数,否则事情不会这么简单
我们还有另外一个问题:怎么保证这个方法筛选后的数字是一定是质数,不多也不少呢?
| 原因 | 说明 |
|---|---|
| 所有合数都有一个小于它本身的质因数 | 所以它们一定会被前面的质数标记 |
| 如果一个数没有被标记 | 说明它没有这样的质因数 → 它只能是质数 |
好了,埃拉托斯特尼筛法(Sieve of Eratosthenes)的实现到此为止。
3 我们进入题目所给函数的实现
public:int countPrimes(int n){auto it = lower_bound(primes.begin(), primes.end(), n);return it - primes.begin();}1. lower_bound 函数的作用:
lower_bound(primes.begin(), primes.end(), n)是 C++ 标准库中的算法。- 它在已排序的数组
primes中查找第一个大于等于n的元素的位置,这是因为我们已经在primes数组中计算了达到5e6数值的质数,所以我们只需要查询即可
2. it - primes.begin() 的作用:
- 这是计算从
primes开始到it的距离(即下标差)。 - 因为
primes是按升序排列的 - 且
vector<int> primes;是一个未初始化的std::vector - 初始状态:长度为 0,容量也为 0。
- 内容:没有任何元素。
- 我们利用push把元素塞入primes数组,塞入多少个元素,数组就有多少个元素
- 所以这个差值就是小于
n的质数个数。
真是一个十分简单的题目呢,今天的文章不废多少劲就可以轻易理解与应用
现在,我把可视化代码献给各位
<!DOCTYPE html>
<html lang="zh-CN">
<head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>埃氏筛可视化(全局初始化 + lower_bound 计数)</title><link rel="stylesheet" href="style.css" /><style>.panel { max-width: 1100px; margin: 0 auto; }.row { display:flex; gap:12px; align-items:center; flex-wrap:wrap; }.grid { display:grid; grid-template-columns: repeat(auto-fill, 36px); gap:6px; align-content:start; }.cell { width:36px; height:36px; border:1px solid #cbd5e1; border-radius:6px; display:flex; align-items:center; justify-content:center; background:#fff; font: 12px/1.2 Consolas, monospace; }.cell.cur { outline:3px solid #3b82f6; background:#dbeafe; }.cell.kill { background:#fee2e2; color:#991b1b; text-decoration: line-through; }.cell.prime { background:#dcfce7; color:#166534; border-color:#86efac; font-weight:600; }.code-view { background:#0b1020; color:#e5e7eb; padding:8px 12px; border-radius:6px; overflow:auto; max-height:420px; font-family:Consolas, 'Courier New', monospace; font-size:12px; line-height:1.5; border:1px solid #1f2937; }.code-line { display:block; white-space:pre; padding:0 6px; border-left:3px solid transparent; }.code-lno { color:#6b7280; margin-right:8px; display:inline-block; width:24px; text-align:right; user-select:none; }.code-line.active { background:rgba(59,130,246,0.15); border-left-color:#3b82f6; }.meta { font-size:13px; color:#374151; }.badge { display:inline-block; padding:2px 6px; border-radius: 10px; background:#eef2ff; color:#4338ca; margin-left:6px; font-size:12px; }</style>
</head>
<body><div class="panel"><h1>埃氏筛可视化(与给定 C++ 代码逐行同步)</h1><div class="row"><label>N (可视化上限): <input type="number" id="sN" value="120" min="10" max="500" style="width:90px"></label><label>n (统计 < n 的质数个数): <input type="number" id="sQuery" value="100" min="0" max="500" style="width:100px"></label><button id="sBuild">Build</button><button id="sRun">Run</button><button id="sStep">Step</button><button id="sPause">Pause</button><button id="sReset">Reset</button><label>Speed: <input type="range" id="sSpeed" min="60" max="1200" value="300" style="width:140px"></label><span id="sInfo" class="meta">Step: 0/0</span></div><div class="row" style="align-items:flex-start; margin-top:10px;"><div style="flex:1; min-width:420px;"><h3>筛表(0..N-1)</h3><div id="sGrid" class="grid"></div><div class="meta" style="margin-top:6px;">i: <span id="si">-</span> | j: <span id="sj">-</span> | 已确认质数数:<span id="sPrimeCnt">0</span><span class="badge" id="sStatus">-</span></div></div><div style="min-width:380px;"><h3>代码(C++)</h3><pre class="code-view" id="code"><code>
<span class="code-line" data-line="1"><span class="code-lno">1</span>vector<int> primes;</span>
<span class="code-line" data-line="2"><span class="code-lno">2</span>static constexpr int MAXN = 5e6 + 1;</span>
<span class="code-line" data-line="3"><span class="code-lno">3</span></span>
<span class="code-line" data-line="4"><span class="code-lno">4</span>auto init = []{</span>
<span class="code-line" data-line="5"><span class="code-lno">5</span> bool is_prime[MAXN];</span>
<span class="code-line" data-line="6"><span class="code-lno">6</span> fill(is_prime, is_prime + MAXN, true);</span>
<span class="code-line" data-line="7"><span class="code-lno">7</span> is_prime[0] = is_prime[1] = false;</span>
<span class="code-line" data-line="8"><span class="code-lno">8</span> for (int i = 2; i < MAXN; i++) {</span>
<span class="code-line" data-line="9"><span class="code-lno">9</span> if (is_prime[i]) {</span>
<span class="code-line" data-line="10"><span class="code-lno">10</span> primes.push_back(i);</span>
<span class="code-line" data-line="11"><span class="code-lno">11</span> for (long long j = 1LL * i * i; j < MAXN; j += i) {</span>
<span class="code-line" data-line="12"><span class="code-lno">12</span> is_prime[j] = false;</span>
<span class="code-line" data-line="13"><span class="code-lno">13</span> }</span>
<span class="code-line" data-line="14"><span class="code-lno">14</span> }</span>
<span class="code-line" data-line="15"><span class="code-lno">15</span> }</span>
<span class="code-line" data-line="16"><span class="code-lno">16</span> return 0;</span>
<span class="code-line" data-line="17"><span class="code-lno">17</span>}();</span>
<span class="code-line" data-line="18"><span class="code-lno">18</span></span>
<span class="code-line" data-line="19"><span class="code-lno">19</span>class Solution{</span>
<span class="code-line" data-line="20"><span class="code-lno">20</span>public:</span>
<span class="code-line" data-line="21"><span class="code-lno">21</span> int countPrimes(int n){</span>
<span class="code-line" data-line="22"><span class="code-lno">22</span> auto it = lower_bound(primes.begin(), primes.end(), n);</span>
<span class="code-line" data-line="23"><span class="code-lno">23</span> return it - primes.begin();</span>
<span class="code-line" data-line="24"><span class="code-lno">24</span> }</span>
<span class="code-line" data-line="25"><span class="code-lno">25</span>};</span></code></pre></div></div></div><script>(function(){const sN = document.getElementById('sN');const sQuery = document.getElementById('sQuery');const sBuild = document.getElementById('sBuild');const sRun = document.getElementById('sRun');const sStep = document.getElementById('sStep');const sPause = document.getElementById('sPause');const sReset = document.getElementById('sReset');const sSpeed = document.getElementById('sSpeed');const sInfo = document.getElementById('sInfo');const g = document.getElementById('sGrid');const si = document.getElementById('si');const sj = document.getElementById('sj');const sPrimeCnt = document.getElementById('sPrimeCnt');const sStatus = document.getElementById('sStatus');const code = document.getElementById('code');const codeLines = code.querySelectorAll('.code-line');function hl(lines){const S = new Set(lines);codeLines.forEach(el=>{const ln = Number(el.getAttribute('data-line'));el.classList.toggle('active', S.has(ln));})}const st = { N:120, query:100, isPrime:[], primes:[], steps:[], idx:-1, running:false, paused:false, spd:300 };function gridBuild(){g.innerHTML='';g.style.gridTemplateColumns = `repeat(${Math.min(12, st.N)}, 36px)`;for(let x=0;x<st.N;x++){const d=document.createElement('div');d.className='cell'; d.id='cell-'+x; d.textContent=String(x);g.appendChild(d);}}function cell(x){ return document.getElementById('cell-'+x); }function addStep(s){ st.steps.push(s); }function build(){st.N = Math.max(10, Math.min(500, Number(sN.value)||120));st.query = Math.max(0, Math.min(500, Number(sQuery.value)||0));st.isPrime = Array(st.N).fill(true);if (st.N>0) st.isPrime[0]=false; if (st.N>1) st.isPrime[1]=false;st.primes = [];st.steps = []; st.idx=-1; sPrimeCnt.textContent='0'; sStatus.textContent='-'; si.textContent='-'; sj.textContent='-';gridBuild();// 代码对应步骤addStep({t:'alloc'}); // 5addStep({t:'fill_true'}); // 6addStep({t:'set01'}); // 7for(let i=2;i<st.N;i++){addStep({t:'i_begin', i}); // 8addStep({t:'if_check', i}); // 9if(st.isPrime[i]){addStep({t:'push_prime', i}); // 10// 预生成 j 序列let start=i*i; if(start>=st.N) { addStep({t:'i_end', i}); continue; }addStep({t:'j_begin', i, j:start}); // 11for(let j=start;j<st.N;j+=i){addStep({t:'hit', i, j}); // 12st.isPrime[j]=false; // 更新用于后续 if_check}addStep({t:'j_end', i});}addStep({t:'i_end', i}); // 14/15}// countPrimes(n)addStep({t:'lower_bound'}); // 22addStep({t:'ret'}); // 23sInfo.textContent=`Step: 0/${st.steps.length}`;hl([4,5,6,7]);}function apply(k){const s = st.steps[k]; if(!s) return;switch(s.t){case 'alloc': hl([4,5]); sStatus.textContent='声明 is_prime[MAXN]'; break;case 'fill_true': hl([6]); for(let x=0;x<st.N;x++){ cell(x).classList.remove('kill','prime','cur'); } break;case 'set01': hl([7]); if(st.N>0) cell(0).classList.add('kill'); if(st.N>1) cell(1).classList.add('kill'); break;case 'i_begin': hl([8]); si.textContent=s.i; sj.textContent='-'; markCur(s.i); break;case 'if_check': hl([9]); // nothing visualbreak;case 'push_prime': hl([10]); cell(s.i).classList.add('prime'); st.primes.push(s.i); sPrimeCnt.textContent=String(st.primes.length); break;case 'j_begin': hl([11]); sj.textContent=s.j; markCur(s.i, s.j); break;case 'hit': hl([12]); sj.textContent=s.j; const c=cell(s.j); if(c) c.classList.add('kill'); break;case 'j_end': hl([13]); break;case 'i_end': hl([14,15]); unCur(); break;case 'lower_bound': hl([21,22]); sStatus.textContent=`lower_bound(n=${st.query})`; highlightQuery(st.query); break;case 'ret': hl([23]); const cnt = st.primes.filter(p=>p<st.query).length; sStatus.textContent=`return ${cnt}`; break;}}function markCur(i, j){unCur(); const ci=cell(i); if(ci) ci.classList.add('cur'); if(j!=null){ const cj=cell(j); if(cj) cj.classList.add('cur'); }}function unCur(){ g.querySelectorAll('.cell.cur').forEach(el=>el.classList.remove('cur')); }function highlightQuery(n){g.querySelectorAll('.cell').forEach(el=>el.style.outline='');const idx = Math.min(Math.max(0, n-1), st.N-1);const el = cell(idx); if(el) el.style.outline='3px dashed #f59e0b';}function replayTo(idx){// reset visuals but keep precomputed steps stategridBuild(); st.isPrime = Array(st.N).fill(true); if (st.N>0) st.isPrime[0]=false; if (st.N>1) st.isPrime[1]=false; st.primes=[]; sPrimeCnt.textContent='0'; sStatus.textContent='-'; si.textContent='-'; sj.textContent='-';for(let i=0;i<=idx;i++) apply(i);st.idx = idx; sInfo.textContent=`Step: ${st.idx+1}/${st.steps.length}`;}function sleep(ms){ return new Promise(r=>setTimeout(r, ms)); }async function run(){ if(st.running) return; st.running=true; try{ while(st.idx < st.steps.length-1){ if(st.paused){ await sleep(40); continue; } replayTo(st.idx+1); await sleep(st.spd); } } finally { st.running=false; } }sBuild.addEventListener('click', ()=>{ build(); });sRun.addEventListener('click', ()=>{ if(!st.steps.length) build(); run(); });sStep.addEventListener('click', ()=>{ if(!st.steps.length) build(); if(st.idx<st.steps.length-1) replayTo(st.idx+1); });sPause.addEventListener('click', ()=>{ st.paused=!st.paused; sPause.textContent = st.paused ? 'Continue':'Pause'; });sReset.addEventListener('click', ()=>{ st.steps=[]; st.idx=-1; gridBuild(); sInfo.textContent='Step: 0/0'; hl([]); });sSpeed.addEventListener('input', ()=>{ const v = Number(sSpeed.value); if(Number.isFinite(v)) st.spd=v; });build();})();</script>
</body>
</html>