Spotify:递归嵌入与聚类（四）

1. 引言

文章来源：Recursive Embedding and Clustering

摘要 大量多样化的数据给聚类带来了诸多挑战，但通过结合降维、递归和监督机器学习的新颖方法，我们取得了显著成果。利用该算法的一部分，我们能够更深入地理解这些聚类存在的原因，从而使用户研究人员和数据科学家能够更快地改进、完善和迭代他们试图解决的问题。锦上添花的是，通过这样做，我们最终拥有了一个可解释性层来验证我们的发现，这反过来又允许我们的用户研究人员和数据科学家进行更深入的探索。

了解我们的用户对我们来说非常重要——更好地了解他们的一种方式是观察他们的使用行为并识别相似之处，从而形成聚类。这不是一项容易的任务。我们应该使用什么数据？什么算法？我们如何提供价值？

有许多既定的数据聚类方法——例如，主成分分析 (PCA) 和 k-均值——但我们需要一种既能帮助我们找到显著聚类，又能解释这些聚类存在原因的方法，从而使我们能够迎合特定的用户群体。因此，我们寻求开发一种新方法。

当试图回答与用户相关的问题时，数据可能来自不熟悉的、定义松散的来源，需要仔细处理（例如，我们第一次收到调查回复、新的数据端点、预处理数据等）。在你的脑海深处，你可以听到一位数据科学家在问问题：

• 每个答案的确切定义是什么？
• 这个样本的分布正确吗？
• 一千……你说了多少列？！

尝试用经典方法解决这些问题可能会导致数百张摘要表、无法大规模工作的方法，最重要的是，无法解释我们的分析。

因此，我们踏上了不同的征程，首先帮助我们的数据科学家解决大规模聚类的更普遍问题，然后验证和传达他们的结果。我们最终确定了四个步骤来应对这些挑战：

1. 使数据易于管理。
2. 进行聚类。
3. 模型可解释性
4. 数据可视化

2. 方法

2.1 使数据易于管理

为了使数据更易于处理，我们通常会尝试将其可视化。然而，数千个变量很难看清。所以我们使用某种形式的降维。

这时我们第一次碰壁了。我们的数据看起来像一团模糊的东西。圆形的。而且模糊的。那该怎么办呢？

在本节的大部分内容中，我将用 MNIST（或修改后的国家标准与技术研究院）数据集来说明我们解决问题的方法。MNIST 有 784 个维度来表示手写数字 0 到 9。

在数据科学 101 中，你将降维等同于 PCA。以下是将其应用于 MNIST 时的样子：

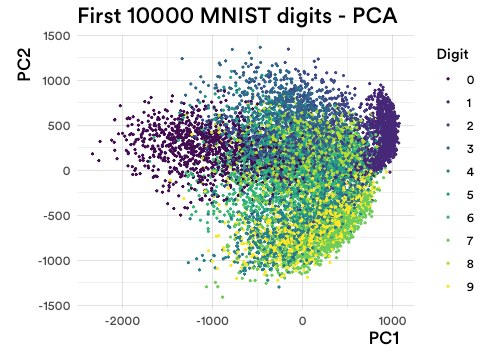
图 1：MNIST 数据集中前 10,000 个手写数字的 PCA 投影。

你明白我的意思了吗？圆形的。而且模糊的。去除所有代表真实情况的颜色，它变得更难辨认。而在现实生活中，我们不知道是否存在聚类！

主要问题是，由于维度太多，所有数据都“处于边缘”，也就是“维度灾难”。

幸运的是，在过去的几年里，这个领域取得了巨大的进步。这些进步使得这种灾难变得不那么相关。我们尝试了一些新的策略，但我们最终选择的是 UMAP（或均匀流形逼近与投影，此处）。我将使用与之前相同的数据向你展示原因：

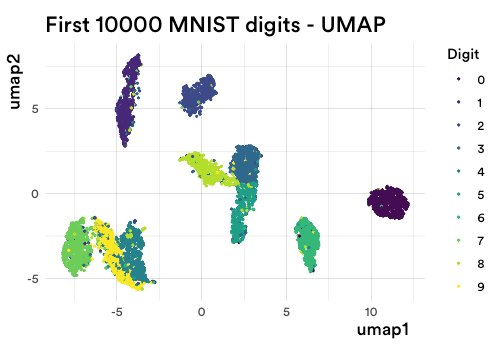
图 2：MNIST 数据集中前 10,000 个手写数字的 UMAP。

不再模糊。不再圆形。里面实际上有一些结构！

所以现在我们完成了第一步。答案是，使用 UMAP。

2.2 聚类

什么使聚类变得好？我们认为：

• 如果聚类存在，一个点就属于一个聚类。
• 如果你需要聚类的参数，让它们是直观的。
• 聚类应该稳定，即使改变数据的顺序或起始条件。

你知道哪个算法不符合这三个标准吗？数据科学 中最受欢迎的 k-均值。

让我再次用上面的图 2（来自 UMAP）向你展示。我运行了 $k$-均值，其中 $k=6$。因为在图 2 中，有六个清晰定义的点群（或聚类），对吗？

类似于以下内容：

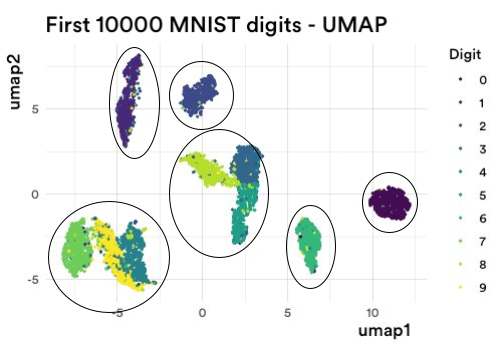
图 3：直观地将 UMAP 聚合为六个聚类。

然而，k-均值做了这个？！

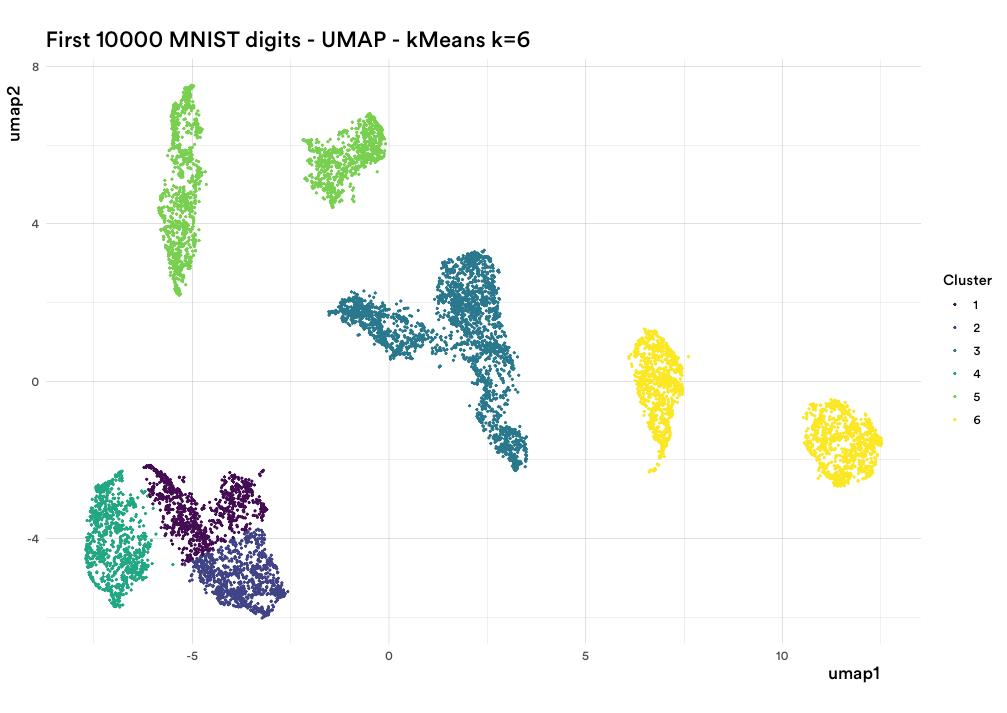
图 4：在 UMAP 上运行 k-均值，期望得到六个聚类的结果。

这是你脑海中的数据科学家在看到上面这张图片时所做的事情：

(╯°□°)╯︵ ┻━┻

然而，有一种算法符合上述标准，并且很好地解决了这个问题，那就是 HDBSCAN（或基于密度的分层空间聚类应用与噪声）。以下是比较：

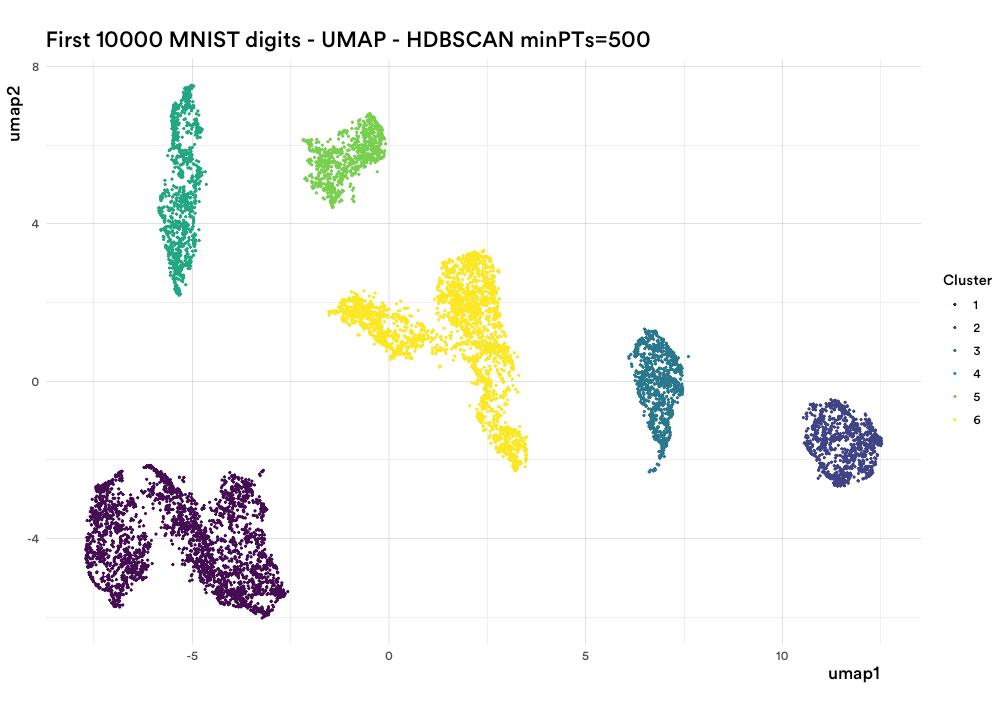
图 5：HDBSCAN 在最小点参数设置为 500 时运行的结果。

你的数据科学家现在可以把桌子放下了……

┬─┬ノ( º _ ºノ)

所以看来我们找到了 UMAP 的一个好伙伴，尽管也存在其他选择，比如高斯混合模型或 Genie 聚类。但即便如此，一些聚类显然还有一些内部结构。

这时我们完全偏离了轨道。如果我们放大呢？我们如何放大？放大意味着什么？我们什么时候放大？

2.2.1 UMAP

回答上述问题需要增加算法的复杂性。

UMAP 是一种在进行降维时试图保持数据局部和全局结构的算法。我们认为，通过将自己限制在一个聚类中，我们可以在某种程度上改变“全局”和“局部”对该特定数据位的含义。

UMAP 的主要功能就是将已经以数字向量形式存在的高维数据，转换成维度更低的数字向量。
MNIST 数据集中的每张手写数字图片，最初都是一个 784 维的数字向量（因为图片是 28x28 像素，每个像素的亮度值就是一个数字）。UMAP 的作用就是将这些 784 维的数字向量，降维成 2 维或 3 维的数字向量，以便在二维平面上进行可视化。

这就是我们放大的想法：选择一个聚类，只保留属于该聚类的原始数据点，然后只对它重复该过程。

也许用一个例子更容易理解。例如，取上面图 5 中间的黄色聚类。我们分离出属于该聚类的数据点，然后对它们运行 UMAP 和 HDBSCAN。

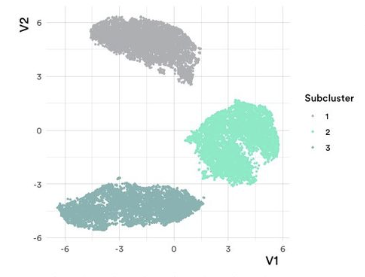
图 6：对图 5 中黄色聚类应用 UMAP 后进行递归聚类。

Eureka!

现在很清楚，这个中间聚类实际上有三个“子聚类”，每个子聚类都代表了原始数据的一种细微差别。在这种情况下，它们是手写数字。所以让我们看看每个子聚类所代表的平均图像。

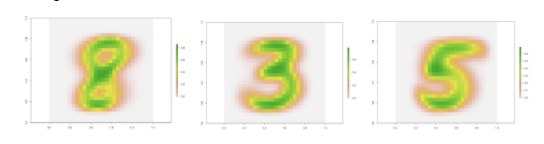
图 7：图 6 中每个聚类的平均重建图像。

太迷人了！数字 8、3 和 5 都有一些共同点。它们有三个由半圆形连接的水平部分。这些半圆形如何绘制区分了它们。而这种更清晰的理解只有在放大时才会出现。

更令人着迷的是，我们可以对原始图片中的所有聚类都这样做，即使是那些看起来没有任何结构的聚类。比如最右边的那个，蓝色圆圈。

这是蓝色圆圈 + UMAP + HDBSCAN + 平均图像：

图 8：在图 5 中的蓝色聚类上应用递归 UMAP 找到的五个聚类中的平均重建图像。

这是一个零的集合，它们通过绘制的圆度和倾斜度来区分。

然而，需要注意的一点是，这个过程可能非常耗时。此外，你需要在开始时确定要放大的深度。你真的想放大一个只占你数据 1% 的聚类吗？这取决于你和你想实现的目标。

2.3 模型的可解释性

到目前为止，我们已经能够使数据易于管理，并且也找到了一些聚类。我们还利用了算法的能力来发现更精细的结构。但为了做到这一点，我们反复运行了一些非常复杂的算法。理解算法为何如此运作并非人类能轻易做到；它们是高度非线性的过程，层层堆叠。

但也许一些非人类的统计和机器学习过程可以理解它。

我们有数据，并且通过上述过程，我们为每个数据点都找到了聚类——数据和自动生成的标签。这是一个典型的机器学习分类问题！幸运的是，模型可解释性（XAI，或可解释人工智能）方面已经取得了惊人的发展。那么，如果我们构建一个模型并使用 XAI 来理解我们的 UMAP + HDBSCAN + 递归正在做什么呢？

在我们的特定案例中，我们决定使用 XGBoost 作为每个聚类的一对多模型。这使得训练非常快速和准确，并且还集成了 SHAP（或 Shapley 加性解释，此处）值以实现可解释性。

通过查看 SHAP 摘要图，我们可以深入了解我们堆叠过程的内部运作。然后，我们可以深入研究每个重要特征，评估每个聚类的有效性，并不断完善我们对数据和用户的理解。

我们还可以使用并在生产中部署该模型，而无需再次运行 UMAP 和 HDBSCAN。我们现在可以使用来自我们管道的原始数据。这再简单不过了，不是吗？

2.4 可视化

一旦聚类建立良好，我们就可以查看其他数据源，如人口统计数据、平台使用情况等，以进一步微调我们对用户身份的理解。这通常会涉及用户研究、市场研究和数据科学的进一步工作。

但最终，你将获得关于每个聚类的一些非常确凿的证据。

想象一下一个演示文稿，其中显示了以下内容：

• 你拥有一些数据驱动的、信息充分的、经过彻底研究的人口聚类。
• 你有 SHAP 图表，显示了模型为何选择将用户放入某个聚类。
• 你对这些用户进行了更精细的调整研究，这些研究由原始数据驱动，并辅以有针对性的用户和市场研究。每个都有自己的幻灯片。
• 你知道每个聚类在人群中的重要性。
• 你还可以查看原始调查范围之外的其他问题，并逐个聚类地回答它们。也许有一部分人群会比其他人更容易接受某个特定功能？

3. 结论和后续工作

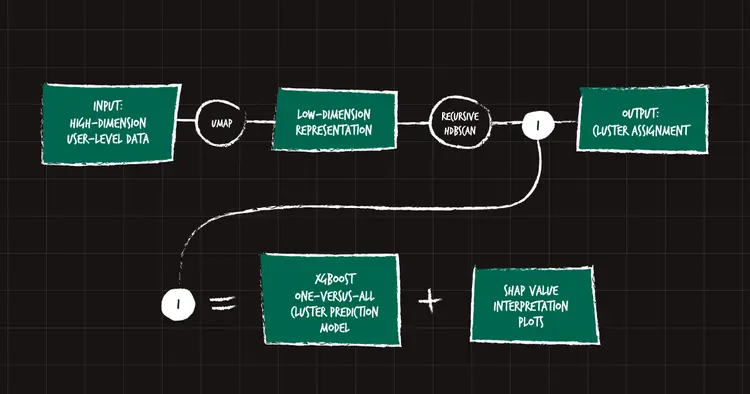
为了回顾整个过程，这里有一个图表：

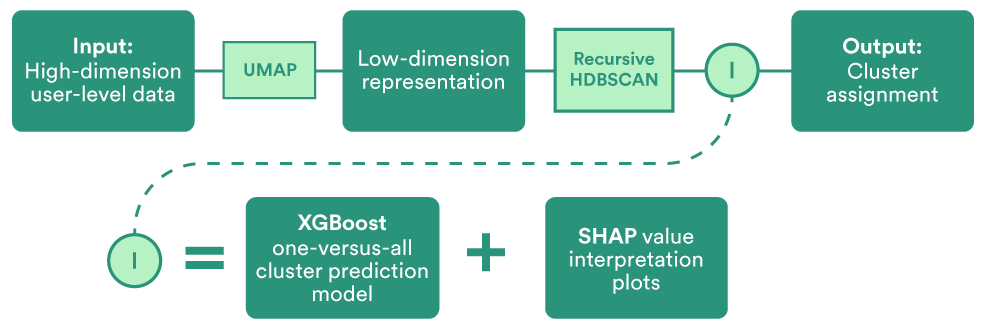
图 9：表示完整递归嵌入和聚类过程的图表。

这个过程包含一些明确定义的步骤，其中大部分以前都使用过。然而，我们在这个过程中的主要贡献是递归（放大）和构建可解释性层的新颖想法。这使得我们从一开始就能更精细、更深入地了解我们的用户。反过来，更好的信息可以对每个数据驱动的、但也经过定性评估的用户群体进行更有针对性的研究，最终促成开发出更好的产品和体验，造福所有用户。