ego(9)---ego-planner中的动力学仿真
动力仿真的总体流程
ego 中的无人机动力仿真写得还是非常细致的,运用电机推力和力矩与转速的公式来更新电机转速,然后再根据电机转速来计算无人机的状态,然后再根据无人机的状态去反推里程计与 imu 的话题数据发布。
主要就是这三个文件,这三个文件的作用如下框图所示:
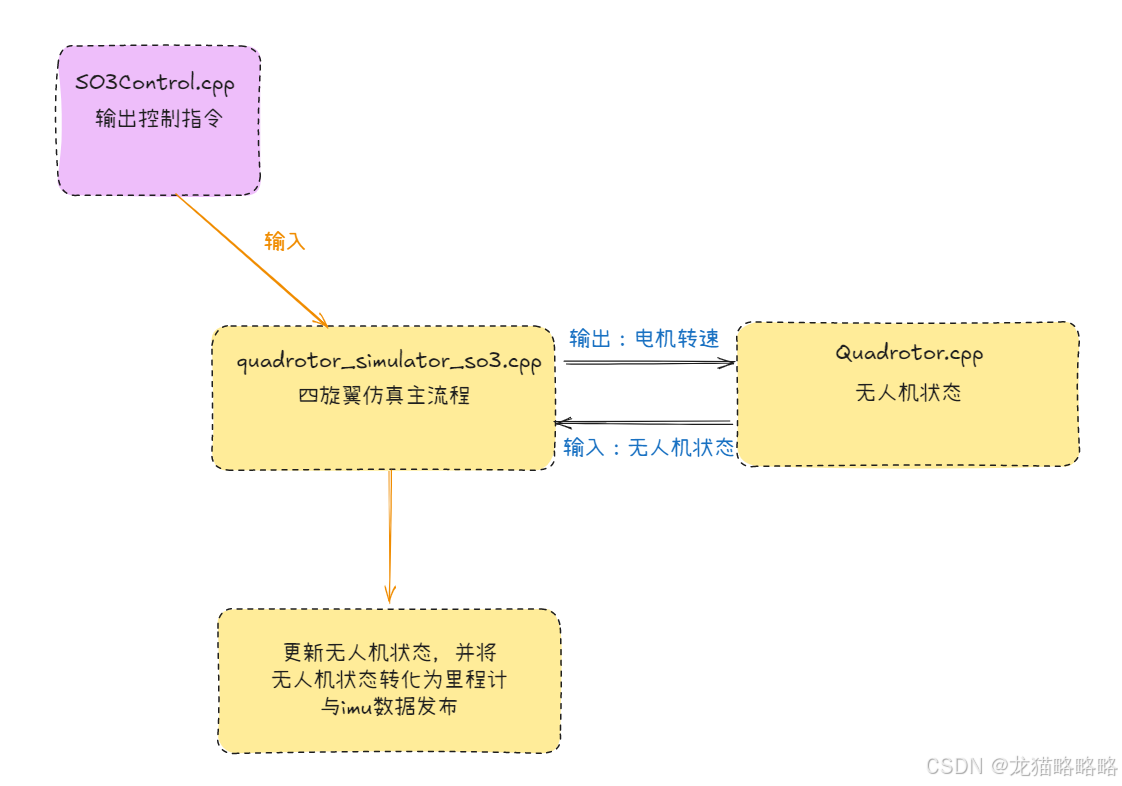
计算控制指令
在 ego 中,输出的控制指令包括两个部分,一个是力矩,一个是力矩的方向,也就是角度,最终是单独将方向转化为了四元数来发布出来,这部分内容在 SO3Control.cpp 中。
控制指令的力矩生成根据位置,速度,加速度各控制量叠加生成。
初始推力设置为重力:
force_ = mass_ * g_ * Eigen::Vector3d(0, 0, 1); // 初始推力--设置为重力之后叠加位置,速度,加速度控制量:
// 初始推力累加各控制量
if ( flag_use_pos ) force_.noalias() += kx.asDiagonal() * (des_pos - pos_);
if ( flag_use_vel ) force_.noalias() += kv.asDiagonal() * (des_vel - vel_);
if ( flag_use_acc ) force_.noalias() += mass_ * ka.asDiagonal() * (des_acc - acc_) + mass_ * (des_acc);在叠加后,减去重力,得到纯姿态的力矩控制,之后检测是否超过最大倾角 45 度,如果超过则进行调整:
// Limit control angle to 45 degree
double theta = M_PI / 2; // 限制飞机最大倾角为 45 度
double c = cos(theta);
Eigen::Vector3d f;
f.noalias() = force_ - mass_ * g_ * Eigen::Vector3d(0, 0, 1); // 去除重力分量后的力
// 检测当前控制力的方向是否超过倾角限制 如果超过,则修正控制力
if (Eigen::Vector3d(0, 0, 1).dot(force_ / force_.norm()) < c)
{
double nf = f.norm();
double A = c * c * nf * nf - f(2) * f(2);
double B = 2 * (c * c - 1) * f(2) * mass_ * g_;
double C = (c * c - 1) * mass_ * mass_ * g_ * g_;
double s = (-B + sqrt(B * B - 4 * A * C)) / (2 * A);
force_.noalias() = s * f + mass_ * g_ * Eigen::Vector3d(0, 0, 1);
}
// Limit control angle to 45 degree之后将控制量的姿态单独提取出来,转化为四元数:
// 求解控制力的姿态四元数(仅表示姿态,力的大小还是由 force_ 来代表)
Eigen::Vector3d b1c, b2c, b3c;
Eigen::Vector3d b1d(cos(des_yaw), sin(des_yaw), 0);if (force_.norm() > 1e-6)
b3c.noalias() = force_.normalized();
else
b3c.noalias() = Eigen::Vector3d(0, 0, 1);b2c.noalias() = b3c.cross(b1d).normalized();
b1c.noalias() = b2c.cross(b3c).normalized();Eigen::Matrix3d R;
R << b1c, b2c, b3c;orientation_ = Eigen::Quaterniond(R);根据控制指令计算电机转速
在无人机动力仿真的主循环中,就是监听控制指令,然后来计算出电机转速。
期望力矩的计算
在获取控制指令,然后根据期望与实际值,生成期望的力矩,都比较容易理解,就按照旋转矩阵来抄公式计算即可(ego 中是使用旋转矩阵进行计算的):
const QuadrotorSimulator::Quadrotor::State state = quad.getState();// Rotation, may use external yaw
Eigen::Vector3d _ypr = uav_utils::R_to_ypr(state.R); // 从旋转矩阵计算欧拉角(yaw,pitch,roll)
Eigen::Vector3d ypr = _ypr;
// 如果使用外部航向角,则修改航向角
if (cmd.use_external_yaw)
ypr[0] = cmd.current_yaw;// 重新计算旋转矩阵
Eigen::Matrix3d R;
R = Eigen::AngleAxisd(ypr[0], Eigen::Vector3d::UnitZ()) * // yawEigen::AngleAxisd(ypr[1], Eigen::Vector3d::UnitY()) * // pitchEigen::AngleAxisd(ypr[2], Eigen::Vector3d::UnitX()); // roll
float R11 = R(0, 0);
float R12 = R(0, 1);
float R13 = R(0, 2);
float R21 = R(1, 0);
float R22 = R(1, 1);
float R23 = R(1, 2);
float R31 = R(2, 0);
float R32 = R(2, 1);
float R33 = R(2, 2);
/*
float R11 = state.R(0,0);
float R12 = state.R(0,1);
float R13 = state.R(0,2);
float R21 = state.R(1,0);
float R22 = state.R(1,1);
float R23 = state.R(1,2);
float R31 = state.R(2,0);
float R32 = state.R(2,1);
float R33 = state.R(2,2);
*/// 提取状态中的角速度
float Om1 = state.omega(0);
float Om2 = state.omega(1);
float Om3 = state.omega(2);// 将期望姿态角(四元数)转化为旋转矩阵
float Rd11 =
cmd.qw * cmd.qw + cmd.qx * cmd.qx - cmd.qy * cmd.qy - cmd.qz * cmd.qz;
float Rd12 = 2 * (cmd.qx * cmd.qy - cmd.qw * cmd.qz);
float Rd13 = 2 * (cmd.qx * cmd.qz + cmd.qw * cmd.qy);
float Rd21 = 2 * (cmd.qx * cmd.qy + cmd.qw * cmd.qz);
float Rd22 =
cmd.qw * cmd.qw - cmd.qx * cmd.qx + cmd.qy * cmd.qy - cmd.qz * cmd.qz;
float Rd23 = 2 * (cmd.qy * cmd.qz - cmd.qw * cmd.qx);
float Rd31 = 2 * (cmd.qx * cmd.qz - cmd.qw * cmd.qy);
float Rd32 = 2 * (cmd.qy * cmd.qz + cmd.qw * cmd.qx);
float Rd33 =
cmd.qw * cmd.qw - cmd.qx * cmd.qx - cmd.qy * cmd.qy + cmd.qz * cmd.qz;// 计算姿态误差相关的Psi值(用于判断位置控制稳定性)
float Psi = 0.5f * (3.0f - (Rd11 * R11 + Rd21 * R21 + Rd31 * R31 +Rd12 * R12 + Rd22 * R22 + Rd32 * R32 +Rd13 * R13 + Rd23 * R23 + Rd33 * R33));// Psi 是期望姿态角与实际姿态角的偏差,位置稳定需要 Psi < 1
float force = 0;
if (Psi < 1.0f) // Position control stability guaranteed only when Psi < 1
force = cmd.force[0] * R13 + cmd.force[1] * R23 + cmd.force[2] * R33;// 姿态误差
float eR1 = 0.5f * (R12 * Rd13 - R13 * Rd12 + R22 * Rd23 - R23 * Rd22 +R32 * Rd33 - R33 * Rd32);
float eR2 = 0.5f * (R13 * Rd11 - R11 * Rd13 - R21 * Rd23 + R23 * Rd21 -R31 * Rd33 + R33 * Rd31);
float eR3 = 0.5f * (R11 * Rd12 - R12 * Rd11 + R21 * Rd22 - R22 * Rd21 +R31 * Rd32 - R32 * Rd31);// 角速度误差,此时角速度期望为0,因此就直接传入当前角速度
float eOm1 = Om1;
float eOm2 = Om2;
float eOm3 = Om3;// 计算陀螺力矩和转动惯量耦合项(来自欧拉动力学方程)
float in1 = Om2 * (I[2][0] * Om1 + I[2][1] * Om2 + I[2][2] * Om3) -Om3 * (I[1][0] * Om1 + I[1][1] * Om2 + I[1][2] * Om3);
float in2 = Om3 * (I[0][0] * Om1 + I[0][1] * Om2 + I[0][2] * Om3) -Om1 * (I[2][0] * Om1 + I[2][1] * Om2 + I[2][2] * Om3);
float in3 = Om1 * (I[1][0] * Om1 + I[1][1] * Om2 + I[1][2] * Om3) -Om2 * (I[0][0] * Om1 + I[0][1] * Om2 + I[0][2] * Om3);
/*
// Robust Control --------------------------------------------
float c2 = 0.6;
float epsilonR = 0.04;
float deltaR = 0.1;
float eA1 = eOm1 + c2 * 1.0/I[0][0] * eR1;
float eA2 = eOm2 + c2 * 1.0/I[1][1] * eR2;
float eA3 = eOm3 + c2 * 1.0/I[2][2] * eR3;
float neA = sqrt(eA1*eA1 + eA2*eA2 + eA3*eA3);
float muR1 = -deltaR*deltaR * eA1 / (deltaR * neA + epsilonR);
float muR2 = -deltaR*deltaR * eA2 / (deltaR * neA + epsilonR);
float muR3 = -deltaR*deltaR * eA3 / (deltaR * neA + epsilonR);
// Robust Control --------------------------------------------
*/
// PD控制律计算期望力矩(M1:滚转力矩, M2:俯仰力矩, M3:偏航力矩)
float M1 = -cmd.kR[0] * eR1 - cmd.kOm[0] * eOm1 + in1; // - I[0][0]*muR1;
float M2 = -cmd.kR[1] * eR2 - cmd.kOm[1] * eOm2 + in2; // - I[1][1]*muR2;
float M3 = -cmd.kR[2] * eR3 - cmd.kOm[2] * eOm3 + in3; // - I[2][2]*muR3;在上述代码中,有一段陀螺力矩与转动惯量耦合项,这部分是参照欧拉动力学方程得来:
M = J·ω̇ + ω × (J·ω)M 是外力矩(控制力矩)
J 是转动惯量矩阵
ω 是角速度向量(机体坐标系下)
ω̇ 是角加速度向量
× 表示向量叉乘
J·ω 表示转动惯量矩阵与角速度的乘积
在上面的控制算法中,需要计算角加速度 ω̇ ,于是可以列出角加速度的公式:
ω̇ = J⁻¹ [ M - (ω × (J·ω)) ]代码中的 in1,in2,in3 就是 (ω × (J·ω))
in1,in2,in3 的求解参照下述过程:
J·ω = [ I₁₁ω₁ + I₁₂ω₂ + I₁₃ω₃ ] = [ Jω₁ ][ I₂₁ω₁ + I₂₂ω₂ + I₂₃ω₃ ] [ Jω₂ ][ I₃₁ω₁ + I₃₂ω₂ + I₃₃ω₃ ] [ Jω₃ ]ω × (J·ω) = | i j k || ω₁ ω₂ ω₃ || Jω₁ Jω₂ Jω₃ |x 轴分量(i 方向):ω₂·Jω₃ - ω₃·Jω₂
y 轴分量(j 方向):ω₃·Jω₁ - ω₁·Jω₃
z 轴分量(k 方向):ω₁·Jω₂ - ω₂·Jω₁x轴分量:in1 = ω₂·Jω₃ - ω₃·Jω₂= ω₂·(I₃₁ω₁ + I₃₂ω₂ + I₃₃ω₃) - ω₃·(I₂₁ω₁ + I₂₂ω₂ + I₂₃ω₃)y轴分量:in2 = ω₃·Jω₁ - ω₁·Jω₃= ω₃·(I₁₁ω₁ + I₁₂ω₂ + I₁₃ω₃) - ω₁·(I₃₁ω₁ + I₃₂ω₂ + I₃₃ω₃)z轴分量:in3 = ω₁·Jω₂ - ω₂·Jω₁= ω₁·(I₂₁ω₁ + I₂₂ω₂ + I₂₃ω₃) - ω₂·(I₁₁ω₁ + I₁₂ω₂ + I₁₃ω₃)上述公式即对应 ego 的代码。
不过也不用死记这部分公式,需要知道的是这部分的作用就是为了补偿无人机旋转时对三轴力矩产生的影响即可。
根据力矩计算转速
在这一部分,比较核心的公式是两个:
推力与电机转速的关系:F = kf * w^2
其中,kf 表示推力系数,F 表示电机的推力,w 表示电机的转速
无人机偏航旋转力矩与转速的关系:M = km * w^2
其中,km 为力矩系数,w 为电机转速。注意,这个公式用于计算偏航的力矩与电机转速的关系,横滚与俯仰有电机本身力矩差直接产生。
先看原始代码:
// 计算电机转速平方(w_sq) 推力与转速的平方成正比 F = kf*w²float w_sq[4];w_sq[0] = force / (4 * kf) - M2 / (2 * d * kf) + M3 / (4 * km);w_sq[1] = force / (4 * kf) + M2 / (2 * d * kf) + M3 / (4 * km);w_sq[2] = force / (4 * kf) + M1 / (2 * d * kf) - M3 / (4 * km);w_sq[3] = force / (4 * kf) - M1 / (2 * d * kf) - M3 / (4 * km);其中 force 是四个电机的总推力,M1,M2,M3 是上面求解到的姿态力矩。
其中比较特殊的是偏航扭力M3,由上面第二个公式得到,每个电机的反扭力就是 M = km * w^2 / 4。
姿态角的力矩需要乘以力臂 d ,于是,单电机与姿态力矩的关系就为 F = M1 / (2*d) 或 F = M2 / (2*d),分别对应横滚与俯仰。
总的推力计算为:
force = F₀ + F₁ + F₂ + F₃
= kf·w₀² + kf·w₁² + kf·w₂² + kf·w₃²
= kf·(w₀² + w₁² + w₂² + w₃²) 然后逐轴分析,单个电机的转速平方就是总推力/(4*kf),再叠加横滚俯仰轴的的力矩 / (2*d*kf),再叠加偏航力矩 / (4*km)。
上述代码中的 w_sq 存储的就是转速的平方,然后再开方即可得到电机转速:
// 开方计算转速 得到转速后,传入 Quadrotor 类中进一步计算飞机状态进行更新Control control;for (int i = 0; i < 4; i++){if (w_sq[i] < 0)w_sq[i] = 0;control.rpm[i] = sqrtf(w_sq[i]);}根据电机转速更新无人机状态
在仿真的流程中,根据上一步计算完电机转速后,就会传入无人机类中,作为输入,再逐步更新无人机状态:
auto last = control;control = getControl(quad, command); // 根据控制指令计算电机转速for (int i = 0; i < 4; ++i){//! @bug might have nan when the input is legalif (std::isnan(control.rpm[i]))control.rpm[i] = last.rpm[i];}quad.setInput(control.rpm[0], control.rpm[1], control.rpm[2],control.rpm[3]); // 输入电机转速quad.setExternalForce(disturbance.f);quad.setExternalMoment(disturbance.m);quad.step(dt); // 更新飞机状态在无人机类的内部,基本就是将上一节的公式反过来,根据转速反过来求解三轴力矩:
// 计算姿态力矩Eigen::Vector3d moments;moments(0) = kf_ * (motor_rpm_sq(2) - motor_rpm_sq(3)) * arm_length_;moments(1) = kf_ * (motor_rpm_sq(1) - motor_rpm_sq(0)) * arm_length_;moments(2) = km_ * (motor_rpm_sq(0) + motor_rpm_sq(1) - motor_rpm_sq(2) -motor_rpm_sq(3));然后再根据力矩计算角速度,加速度,速度与位置。
在主循环中,再将计算得到的无人机状态转化为里程计信息与 imu 信息发布出去:
void
stateToOdomMsg(const QuadrotorSimulator::Quadrotor::State& state,nav_msgs::Odometry& odom)
{odom.pose.pose.position.x = state.x(0);odom.pose.pose.position.y = state.x(1);odom.pose.pose.position.z = state.x(2);Eigen::Quaterniond q(state.R);odom.pose.pose.orientation.x = q.x();odom.pose.pose.orientation.y = q.y();odom.pose.pose.orientation.z = q.z();odom.pose.pose.orientation.w = q.w();odom.twist.twist.linear.x = state.v(0);odom.twist.twist.linear.y = state.v(1);odom.twist.twist.linear.z = state.v(2);odom.twist.twist.angular.x = state.omega(0);odom.twist.twist.angular.y = state.omega(1);odom.twist.twist.angular.z = state.omega(2);
}void
quadToImuMsg(const QuadrotorSimulator::Quadrotor& quad, sensor_msgs::Imu& imu){QuadrotorSimulator::Quadrotor::State state = quad.getState();Eigen::Quaterniond q(state.R);imu.orientation.x = q.x();imu.orientation.y = q.y();imu.orientation.z = q.z();imu.orientation.w = q.w();imu.angular_velocity.x = state.omega(0);imu.angular_velocity.y = state.omega(1);imu.angular_velocity.z = state.omega(2);imu.linear_acceleration.x = quad.getAcc()[0];imu.linear_acceleration.y = quad.getAcc()[1];imu.linear_acceleration.z = quad.getAcc()[2];
}