算法代码讲座6：最小二乘法理论原理、典型案例与MATLAB实现

1.核心思想与数学本质

最小二乘法（Least Squares Method）是一种数学优化方法，其核心思想是通过最小化误差的平方和来寻找数据的最佳函数（参数）。

2.建模流程

已知采样数据 -->选择模型（有线性和非线性之分）-->写出残差平方和的表达式，这就是目标函数--> 最小化目标函数，进行优化求解（线性问题有固定的解析解，非线性问题优化方法多样）-->获得最佳参数。

3.数学模型

对于给定的采样数据点(x(i), y(i)), i=1,2,...,n，寻找函数f(x)，使其最佳的逼近拟合采样数据。

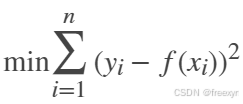
至此，最小二乘的思想和数学模型介绍完毕。

下面对不同类型的最小二乘问题进行介绍和求解，最为经典是线性最小二乘问题。

4.线性最小二乘问题

线性最小二乘问题的基本假设：采样数据x和y呈线性关系。

根据以上假设，表达式可以写成：f(x) = ax + b。

线性最小二乘问题的数学模型就可以写成如下形式：

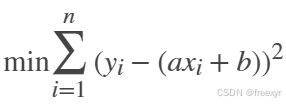
如果以上内容理解起来无压力，可别得意，下面即将晦涩起来，读不懂的同学先去补习一下矩阵论和线性代数的知识哈。

把上述模型改用比较潮流加时髦的矩阵形式，就是这样的：

min ||Y-Xβ||2

其中：

Y是观测值向量(y(1),y(2),...y(n))T，注意，是列向量。

X是设计矩阵：

[1, x(1);

 1, x(2);

 ...

 1, x(n)]

β是参数向量[b;a]，注意，也是列向量哈。

说到这里，不知大家是否有所疑问，好端端的数学表达式为什么非要使用矩阵形式表达？只是为了潮流加时髦吗，No，为了求解方便，请往下看。

5.线性最小二乘问题的求解方法

正规方程法：

β=(XTX)-1XTY

几何解释：线性最小二乘解，等价于在X的列空间中寻找Y的正交投影。

（freexyn：这里补充个知识点：列空间，概念：若A为m*n的矩阵，A的列空间C(A)是A中各列的所有线性组合的集合，也即，A的列向量构成的空间，它是R^m的子空间，在视频15.8有详细讲述）。

6.典型案例

以下提供了弹簧伸长实验的数据：

受力F（N）	0.5	1.0	1.5	2.0	2.5
伸长量x（cm）	1.2	2.1	3.0	4.1	5

根据胡克定律F = kx+b，求弹簧系数k，以及弹簧初始长度b。

Matlab程序代码如下：

% 弹簧伸长实验数据

F = [0.5, 1.0, 1.5, 2.0, 2.5]; %受力F（N）

x = [1.2, 2.1, 3.0, 4.1, 5.0]; % 伸长(cm)

% 构建设计矩阵

X = [ones(size(F)); F]';

% 求解正规方程

beta = (X'*X) \ (X'*x');

% 提取参数

k = 1/beta(2) % 弹簧系数

b = beta(1) % 初始长度

运行结果：

k =

    0.5208

b =

    0.2000

% 计算预测值

x_pred = X * beta;

% 可视化

figure;

scatter(F, x, 50, 'filled', 'MarkerFaceColor', [0.2 0.6 0.9]);

hold on;

plot(F, x_pred, 'r-', 'LineWidth', 2);

xlabel('力 F (N)');

ylabel('伸长 x (cm)');

title('弹簧伸长实验 - 最小二乘拟合');

legend('实验数据', sprintf('拟合直线: x = %.2f + %.3fF', b, 1/k),...

       'Location', 'northwest');

grid on;

运行结果：

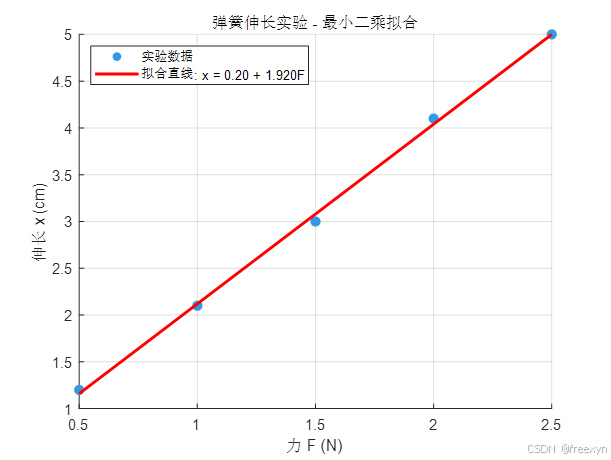
% 计算残差

residuals = x - x_pred';

SSE = sum(residuals.^2) % 残差平方和

SST = sum((x - mean(x)).^2); % 总平方和

R_squared = 1 - SSE/SST % 决定系数

运行结果：

SSE =

    0.0120

R_squared =

    0.9987

7.弹簧实验结果分析

根据上述求解结果：弹簧系数 k = 0.5208N/cm，初始长度 b = 0.2 cm，决定系数 R² = 0.9987，拟合直线几乎完美通过数据点（R²接近1），初始长度接近0，符合物理实际问题背景，弹簧系数k≈0.5 N/cm，符合预期。

8.Matlab工具箱的求解工具

根据数据形式多样化，以及模型表达式较复杂等情况，Matlab提供了多种建模和求解的工具箱工具，大概包括：

（1）曲线拟合工具箱

（这个工具箱在视频系列23：拟合篇有具体讲述）

编程拟合示例：

fit_type = fittype('a*exp(b*x)'); %模型

fitted_model = fit(x', y', fit_type, 'StartPoint', [1, 0.01]); %求解，默认使用最小二乘法

（2）统计与机器学习工具箱

编程示例：

mdl = fitlm(X, Y, 'VarNames', {'Area', 'Rooms', 'Age', 'Price'}); % 创建线性回归模型，默认使用最小二乘法

Y_pred = predict(mdl, X_new); % 进行预测

（3）优化工具箱（非线性最小二乘）

（这个工具箱在视频系列22：优化篇有具体讲述）

编程示例：

% 定义目标函数

fun = @(beta) sum((Y - beta(1)*exp(beta(2)*X).^2);

% 求解优化问题

options = optimoptions('fminunc', 'Algorithm', 'quasi-newton'); %算法可选

beta_opt = fminunc(fun, beta0, options);

9.应用价值

最小二乘法作为最基础的回归分析方法，其核心价值在于：

数学基础坚实：具有清晰的几何解释和统计性质。

实现简单高效：线性问题有解析解。

扩展性强：可推广到非线性、正则化、鲁棒估计。

核心公式：β=(XTX)-1XTY

这一简洁而强大的公式，已成为数据分析的基石工具。

相关文章推荐

Matlab算法代码速成5：Matlab求解分段微分方程编程示例https://blog.csdn.net/freexyn/article/details/150142545?spm=1011.2415.3001.5331Matlab自学笔记六十五：解方程的数值解法（代码速成）https://blog.csdn.net/freexyn/article/details/149672081?spm=1011.2415.3001.5331Matlab自学笔记六十二：求解三角函数方程的通解周期解https://blog.csdn.net/freexyn/article/details/149180676?spm=1011.2415.3001.5331Matlab自学笔记五十七：符号运算、可变精度运算、双精度浮点型运算，三种运算精度的概念、比较、选择和应用https://blog.csdn.net/freexyn/article/details/148409914?spm=1011.2415.3001.5331Matlab自学笔记五十一：（推荐）输入参数的数量和可变数量的输入https://blog.csdn.net/freexyn/article/details/147379696?spm=1011.2415.3001.5331Matlab自学笔记四十九：类型识别：判断数据的类型和类别https://blog.csdn.net/freexyn/article/details/146722114?spm=1011.2415.3001.5331End