【OpenGL】openGL常见矩阵

参考博客：https://www.opengl-tutorial.org/cn/beginners-tutorials/tutorial-3-matrices/

一、齐次坐标（Homogeneous coordinates）

目前为止，我们仍然把三维顶点视为三元组(x,y,z)。现在引入一个新的分量w，得到向量(x,y,z,w)。请先记住以下两点（稍后我们会给出解释）：

• 若w == 1，则向量(x, y, z, 1)为空间中的点。
• 若w == 0，则向量(x, y, z, 0)为方向。

（请务必将此牢记在心。）

• 二者有什么区别呢？对于旋转，这点区别倒无所谓。当您旋转点和方向时，结果是一样的。但对于平移（将点沿着某个方向移动）情况就不同了。”平移一个方向”是毫无意义的。

• 齐次坐标使得我们可以用同一个公式对点和方向作运算。

二、变换矩阵（Transformation matrices）

2.1 矩阵简介

简而言之，矩阵就是一个行列数固定的、纵横排列的数表。比如，一个2x3矩阵看起来像这样：

$$\left[\begin{array}{ccc}2& 5& 7\\ 9& 8& 1\end{array}\right]$$

三维图形学中我们只用到4x4矩阵，它能对顶点(x,y,z,w)作变换。这一变换是用矩阵左乘顶点来实现的：

$$\left[\begin{array}{cccc}a& b& c& d\\ e& f& g& h\\ i& j& k& l\\ m& n& o& p\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]=\left[\begin{array}{c}ax+by+cz+dw\\ ex+fy+gz+hw\\ ix+jy+kz+lw\\ mx+ny+oz+pw\end{array}\right]$$

矩阵x顶点（记住顺序！！矩阵左乘顶点，顶点用列向量表示）= 变换后的顶点

这看上去复杂，实则不然。左手指着a，右手指着x，得到_ax_。 左手移向右边一个数b，右手移向下一个数y，得到_by_。依次类推，得到_cz_、dw。最后求和ax + by + cz + dw，就得到了新的x！每一行都这么算下去，就得到了新的(x, y, z, w)向量。

这种重复无聊的计算就让计算机代劳吧。

用C++，GLM表示：

glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.

使用QT可以这样做：

QMatrix4x4 myMatrix;  
QVector4D myVector;  
QVector4D transformVector = myMatrix * myVector;

用GLSL表示：

mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

（还没把这些代码粘贴到程序里调试吗？赶紧试试！）

2.2 平移矩阵（Translation matrices）

平移矩阵是最简单的变换矩阵。平移矩阵是这样的：

$$\left[\begin{array}{cccc}1& 0& 0& X\\ 0& 1& 0& Y\\ 0& 0& 1& Z\\ 0& 0& 0& 1\end{array}\right]$$

其中，X、Y、Z是点的位移增量。

例如，若想把向量(\begin{bmatrix}10 \ 10 \ 10 \ 1\end{bmatrix})沿X轴方向平移10个单位，可得：

$$\left[\begin{array}{cccc}1& 0& 0& 10\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}10\\ 10\\ 10\\ 1\end{array}\right]=\left[\begin{array}{c}1\ast 10+0\ast 10+0\ast 10+10\ast 1\\ 0\ast 10+1\ast 10+0\ast 10+0\ast 1\\ 0\ast 10+0\ast 10+1\ast 10+0\ast 1\\ 0\ast 10+0\ast 10+0\ast 10+1\ast 1\end{array}\right]=\left[\begin{array}{c}10+0+0+10\\ 0+10+0+0\\ 0+0+10+0\\ 0+0+0+1\end{array}\right]=\left[\begin{array}{c}20\\ 10\\ 10\\ 1\end{array}\right]$$

（算算看！一定得亲手算！！）

这样就得到了齐次向量$\left[\begin{array}{c}20\\ 10\\ 10\\ 1\end{array}\right]$！记住，末尾的1表示这是一个点，而不是方向。经过变换计算后，点仍然是点。

下面来看看，对一个代表Z轴负方向的向量作上述平移变换会得到什么结果：

$$\left[\begin{array}{cccc}1& 0& 0& 10\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]=\left[\begin{array}{c}1\ast 0+0\ast 0+0\ast 0+10\ast 0\\ 0\ast 0+1\ast 0+0\ast 0+0\ast 0\\ 0\ast (-1)+0\ast (-1)+1\ast (-1)+0\ast (-1)\\ 0\ast 0+0\ast 0+0\ast 0+1\ast 0\end{array}\right]=\left[\begin{array}{c}0+0+0+0\\ 0+0+0+0\\ 0+0+(-1)+0\\ 0+0+0+0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]$$

那怎么用代码表示平移变换呢？

用C++，GLM表示：

#include <glm/gtx/transform.hpp> // after <glm/glm.hpp>glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result

用QT，QMatrix4x4表示：

//平移x,y,z方向的大小  
QMatrix4x4 MyGLWidget::translateMatrix(float x, float y, float z)  
{  QMatrix4x4 translate_matrix;  translate_matrix.translate(x,y,z);  return translate_matrix;  
}

**用GLSL表示：**呃，实际中我们几乎不用GLSL计算变换矩阵。大多数情况下在C++代码中用glm::translate()算出矩阵，然后把它传给GLSL。在GLSL中只做一次乘法：

vec4 transformedVector = myMatrix * myVector;

2.3、单位矩阵（Identity matrix）

单位矩阵很特殊，它什么也不做。单位矩阵的身份和自然数“1”一样基础而重要，因此在这里要特别提及一下。

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]=\left[\begin{array}{c}1\ast x+0\ast y+0\ast z+0\ast w\\ 0\ast x+1\ast y+0\ast z+0\ast w\\ 0\ast x+0\ast y+1\ast z+0\ast w\\ 0\ast x+0\ast y+0\ast z+1\ast w\end{array}\right]=\left[\begin{array}{c}x+0+0+0\\ 0+y+0+0\\ 0+0+z+0\\ 0+0+0+w\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]$$

用C++表示：

glm::mat4 myIdentityMatrix = glm::mat4(1.0);

用QT表示：

QMatrix4x4 myIdentityMatrix;
myIdentityMatrix.setToIdentity();

2.4 缩放矩阵（Scaling matrices）

缩放矩阵也很简单：

$$\left[\begin{array}{cccc}x& 0& 0& 0\\ 0& y& 0& 0\\ 0& 0& z& 0\\ 0& 0& 0& 1\end{array}\right]$$

例如把一个向量（点或方向皆可）沿各方向放大2倍：

$$\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 2& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]=\left[\begin{array}{c}2\ast x+0\ast y+0\ast z+0\ast w\\ 0\ast x+2\ast y+0\ast z+0\ast w\\ 0\ast x+0\ast y+2\ast z+0\ast w\\ 0\ast x+0\ast y+0\ast z+1\ast w\end{array}\right]=\left[\begin{array}{c}2\ast x+0+0+0\\ 0+2\ast y+0+0\\ 0+0+2\ast z+0\\ 0+0+0+1\ast w\end{array}\right]=\left[\begin{array}{c}2\ast x\\ 2\ast y\\ 2\ast z\\ w\end{array}\right]$$

w还是没变。您也许会问：”缩放一个向量”有什么用？嗯，大多数情况下是没什么用，所以一般不会去缩放向量；但在某些特殊情况下它就派上用场了。（顺便说一下，单位矩阵只是缩放矩阵的一个特例，其(X, Y, Z) = (1, 1, 1)。单位矩阵同时也是旋转矩阵的一个特例，其(X, Y, Z)=(0, 0, 0)）。

用C++表示：

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

用QT表示：

//缩放x,y,z的大小比例  
QMatrix4x4 MyGLWidget::scaleMatrix(float x, float y, float z) {  QMatrix4x4 scale_matrix;  scale_matrix.scale(x,y,z);  return scale_matrix;  
}

2.5、旋转矩阵（Rotation matrices）

旋转矩阵比较复杂。这里略过细节，因为日常应用中，您并不需要知道矩阵的内部构造。 想了解更多，请看“矩阵和四元组常见问题”（这个资源很热门，应该有中文版吧）。

用C++表示：

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

用QT表示：

//默认逆时针angle，负数表示顺时针，绕(0,0,0)->(x,y,z)指向的方向旋转
QMatrix4x4 MyGLWidget::rotateMatrix(float angle,float x,float y,float z) {QMatrix4x4 rotate_matrix;rotate_matrix.rotate(angle,x,y,z);return rotate_matrix;
}

2.6 累积变换

前面已经学习了如何旋转、平移和缩放向量。把这些矩阵相乘就能将它们组合起来，例如：

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

！！！注意！！！这行代码首先执行缩放，接着旋转，最后才是平移。这就是矩阵乘法的工作方式。

变换的顺序不同，得出的结果也不同。您不妨亲自尝试一下：

• 向前一步（小心别磕着爱机）然后左转；
• 左转，然后向前一步

实际上，上述顺序正是你在变换游戏角色或者其他物体时所需的：先缩放；再调整方向；最后平移。例如，假设有个船的模型（为简化，略去旋转）：

• 错误做法：

  • 按(10, 0, 0)平移船体。船体中心目前距离原点10个单位。
  • 将船体放大2倍。以原点为参照，每个坐标都变成原来的2倍，就出问题了。最后您得到的是一艘放大的船，但其中心位于2*10=20。这并非您预期的结果。

• 正确做法：

  • 将船体放大2倍，得到一艘中心位于原点的大船。
  • 平移船体。船大小不变，移动距离也正确。

矩阵-矩阵乘法和矩阵-向量乘法类似，所以这里也会省略一些细节，不清楚的读者请移步矩阵和四元组常见问题 。现在，就让计算机来算：

用C++，GLM表示：

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

用QT表示：

QMatrix4x4 scale_matrix = scaleMatrix(1.0,1.0,0.0);  
QMatrix4x4 translate_matrix = translateMatrix(0.0,0.0,0.0);  QMatrix4x4 rotate_matrix = rotateMatrix(0.0f,0.0f,0.0f,0.0f);  //叠加操作  
QMatrix4x4 transform_matrix = translate_matrix * rotate_matrix * scale_matrix;

用GLSL表示：

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

三、模型（Model）、观察（View）和投影（Projection）矩阵

在接下来的课程中，我们假定您已知如何绘制Blender经典模型小猴Suzanne。

利用模型、观察和投影矩阵，可以将变换过程清晰地分解为三个阶段。虽然此法并非必需（前两课我们就没用这个方法嘛），但采用此法较为稳妥。我们将看到，这种公认的方法对变换流程作了清晰的划分。

3.1 模型矩阵

这个三维模型和可爱的红色三角形一样，由一组顶点定义。顶点的XYZ坐标是相对于物体中心定义的：也就是说，若某顶点位于(0,0,0)，则其位于物体的中心。

我们希望能够移动它，玩家也需要用键鼠控制这个模型。这很简单，只需记住：缩放_旋转_平移就够了。在每一帧中，用算出的这个矩阵去乘（在GLSL中乘，不是在C++中！）所有的顶点，物体就会移动。唯一不动的是世界空间（World Space）的中心。

现在，物体所有顶点都位于_世界空间_。下图中黑色箭头的意思是：从模型空间（Model Space）（顶点都相对于模型的中心定义）变换到世界空间（顶点都相对于世界空间中心定义）。

下图概括了这一过程：

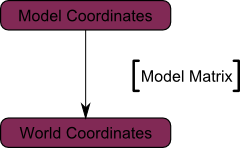
3.2 观察矩阵

这里再引用一下《飞出个未来》：

引擎推动的不是飞船而是宇宙。飞船压根就没动过。

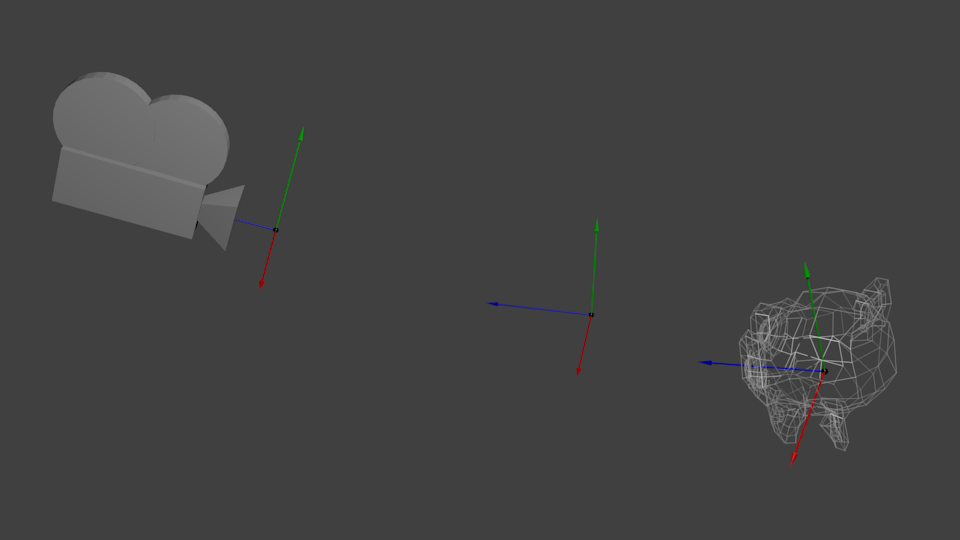
仔细想想，摄像机的原理也是相通的。如果想换个角度观察一座山，您可以移动摄像机也可以……移动山。后者在实际中不可行，在计算机图形学中却十分方便。

起初，摄像机位于世界坐标系的原点。移动世界只需乘一个矩阵。假如你想把摄像机向右（X轴正方向）移动3个单位，这和把整个世界（包括网格）向左（X轴负方向）移3个单位是等效的！脑子有点乱？来写代码吧：

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f, 0.0f));

下图展示了：从世界空间（顶点都相对于世界空间中心定义）到摄像机空间（Camera Space，顶点都相对于摄像机定义）的变换。

趁脑袋还没爆炸，来欣赏一下GLM强大的glm::LookAt函数吧：

glm::mat4 CameraMatrix = glm::LookAt(cameraPosition, // the position of your camera, in world spacecameraTarget,   // where you want to look at, in world spaceupVector        // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);

在QT中是这样的：

//观察矩阵  
QVector3D camera_pos = {4,4,3};  
QVector3D look_dir = {1,0,0};  
QVector3D up_dir = {0,1,0};  //lookAt  
QMatrix4x4 view_matrix;  
view_matrix.lookAt(camera_pos,look_dir,up_dir);

下图解释了上述变换过程：

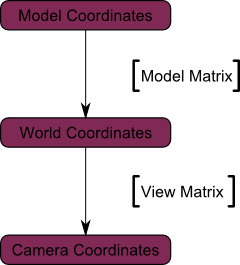
3.3 投影矩阵

现在，我们处于摄像机空间中。这意味着，经历了这么多变换后，现在一个坐标X == 0且Y == 0的顶点，应该被画在屏幕的中心。但仅有x、y坐标还不足以确定物体是否应该画在屏幕上：它到摄像机的距离（z）也很重要！两个x、y坐标相同的顶点，z值较大的一个将会最终显示在屏幕上。

这就是所谓的透视投影（perspective projection）：

好在用一个4x4矩阵就能表示这个投影¹ :

// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(glm::radians(FoV), // The vertical Field of View, in radians: the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)4.0f / 3.0f,       // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?0.1f,              // Near clipping plane. Keep as big as possible, or you'll get precision issues.100.0f             // Far clipping plane. Keep as little as possible.
);

在QT中可以这样使用：

//投影矩阵
float angle = 45;
float aspect = this->width() * 1.0f / this->height();//距离相机的位置，渲染范围：0.1-100
float near_plane = 0.1f;
float far_plane = 100.f;QMatrix4x4 projection_matrix;
projection_matrix.perspective(angle,aspect,near_plane,far_plane);

最后一个变换：

从摄像机空间（顶点都相对于摄像机定义）到齐次坐空间（Homogeneous Space）（顶点都在一个小立方体中定义。立方体内的物体都会在屏幕上显示）的变换。

最后一幅图示：

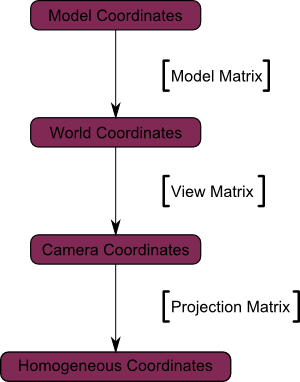
再添几张图，以便大家更好地理解投影变换。投影前，蓝色物体都位于摄像机空间中，红色的东西是摄像机的平截头体（frustum）：这是摄像机实际能看见的区域。

用投影矩阵去乘前面的结果，得到如下效果：

此图中，平截头体变成了一个正方体（每条棱的范围都是-1到1，图不太明显），所有的蓝色物体都经过了相同的变形。因此，离摄像机近的物体就显得大一些，远的显得小一些。这和现实生活一样！

让我们从平截头体的”后面”看看它们的模样：

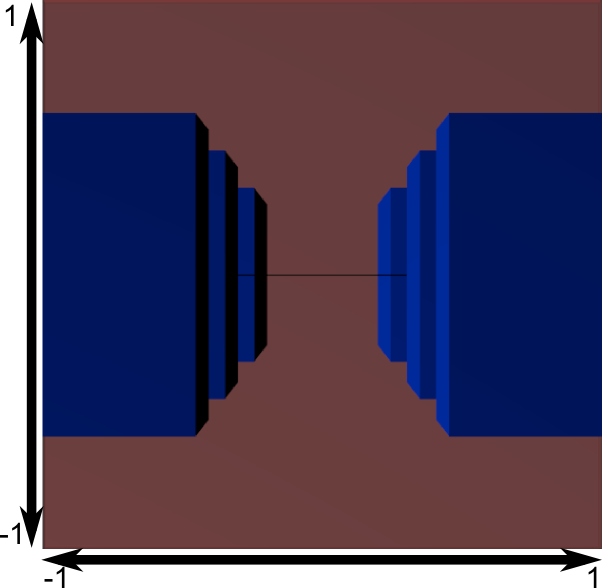
这就是您得到的图像！看上去太方方正正了，因此，还需要做一次数学变换使之适合实际的窗口大小。

这就是实际渲染的图像啦！

复合变换：模型观察投影矩阵（MVP）

再来一连串深爱已久的标准矩阵乘法：

// C++ : compute the matrix
glm::mat4 MVPmatrix = projection * view * model; // Remember : inverted !

// C++ : compute the matrix
QMatrix4x4 MVPmatrix = projection * view * model; // Remember : inverted !

// GLSL : apply it
transformed_vertex = MVP * in_vertex;

四、使用MVP矩阵

保持上一章节的内容不变，我们添加一个doMVP函数，用于生成一个MVP矩阵，当然也可以独立生成M、V、P三个矩阵，然后传入到vertex shader中再计算出MVP矩阵，这里采用后者

• 这里的参数可以自行修改，以理解不同的参数对渲染结果的影响，也可以去官网查询api参数具体的含义

• 上传到shader需要在shader定义uniform变量，同时使用glGetUniformLocation获取对应的uniform变量，注意名称要一一对应，然后使用glUniform*函数上传对应类型的参数

void MyGLWidget::doMVP()
{//模型矩阵QMatrix4x4 model_matrix;model_matrix.setToIdentity();//观察矩阵QVector3D camera_pos = {4,4,3};QVector3D look_dir = {1,0,0};QVector3D up_dir = {0,1,0};//lookAtQMatrix4x4 view_matrix;view_matrix.lookAt(camera_pos,look_dir,up_dir);//投影矩阵float angle = 45;float aspect = this->width() * 1.0f / this->height();//距离相机的位置，渲染范围：0.1-100float near_plane = 0.1f;float far_plane = 100.f;QMatrix4x4 projection_matrix;projection_matrix.perspective(angle,aspect,near_plane,far_plane);//获取uniform变量uniform_model_matrix_location = glGetUniformLocation(shader_program_id,"model_matrix");uniform_view_matrix_location = glGetUniformLocation(shader_program_id,"view_matrix");uniform_projection_matrix_location = glGetUniformLocation(shader_program_id,"projection_matrix");//矩阵传入shaderglUniformMatrix4fv(uniform_model_matrix_location,1,GL_FALSE,model_matrix.data());glUniformMatrix4fv(uniform_view_matrix_location,1,GL_FALSE,view_matrix.data());glUniformMatrix4fv(uniform_projection_matrix_location,1,GL_FALSE,projection_matrix.data());}

这里采用的变化函数doTransform生成对应的Model矩阵，也就是对模型空间内的坐标进行变化，比如平移，缩放，旋转

void MyGLWidget::doTransform()  
{  QMatrix4x4 scale_matrix = scaleMatrix(1.0,1.0,0.0);  QMatrix4x4 translate_matrix = translateMatrix(0.0,0.0,0.0);  QMatrix4x4 rotate_matrix = rotateMatrix(0.0f,0.0f,0.0f,0.0f);  //叠加操作  QMatrix4x4 transform_matrix = translate_matrix * rotate_matrix * scale_matrix;  //获取uniform变量：transform_matrix，从着色器程序获取  uniform_transform_matrix_location = glGetUniformLocation(shader_program_id,"transform_matrix");  //上传uniform变量的4x4矩阵:transform_matrix，不需要转置,4fv结尾含义是4x4矩阵float类型,向量（vector）形式  glUniformMatrix4fv(uniform_transform_matrix_location,1,GL_FALSE,transform_matrix.data());  
}

最后就是，注意在vertex shader中定义对应的uniform变量，这个变量是全局唯一的，类似单例，所以即使重名得到的也是同一个结果：

uniform mat4 transform_matrix;  uniform mat4 model_matrix;  
uniform mat4 view_matrix;  
uniform mat4 projection_matrix;

上述代码加入后，最后运行的结果如下：

五、完整代码

my_glwidget.h

//  
// Created by liuhang on 2025/9/16.  
//  #ifndef OPENGL_LEARNING_MY_GLWIDGET_H  
#define OPENGL_LEARNING_MY_GLWIDGET_H  #include<QOpenGLWidget>  
#include<QOpenGLFunctions>  
#include<QMatrix4x4>  
#include<QTimer>  class MyGLWidget : public QOpenGLWidget,protected QOpenGLFunctions  
{  Q_OBJECT  
public:  explicit MyGLWidget(QWidget* parent = nullptr);  ~MyGLWidget() override;  protected:  void initializeGL() override;  void paintGL() override;  void resizeGL(int w,int h) override;  void doTransform();  void doMVP();  
private:  void loadShader(std::string const& vertex_shader_path,std::string const& fragment_shader_path);  QMatrix4x4 translateMatrix(float x, float y, float z);  QMatrix4x4 scaleMatrix(float x,float y,float z);  QMatrix4x4 rotateMatrix(float angle,float x,float y,float z);  private:  GLuint vertex_array_id;  GLuint vertex_buffer_id;  GLuint vertex_shader_id;  GLuint fragment_shader_id;  GLuint shader_program_id;  GLint uniform_transform_matrix_location;  GLint uniform_model_matrix_location;  GLint uniform_view_matrix_location;  GLint uniform_projection_matrix_location;  float global_i = 0;  QTimer timer;  
};  #endif //OPENGL_LEARNING_MY_GLWIDGET_H

my_glwidget.cpp

//  
// Created by liuhang on 2025/9/16.  
//  #include "my_glwidget.h"  
#include<string>  
#include<fstream>  
#include<sstream>  
#include<iostream>  
#include<filesystem>  
#include<QThread>  
#include<math.h>  static const float vertex_buffer_data[] ={  -1.0f, -1.0f, 0.0f,  1.0f, -1.0f, 0.0f,  0.0f,  1.0f, 0.0f  
};  MyGLWidget::MyGLWidget(QWidget *parent): QOpenGLWidget(parent)  
{  
#if 0  timer.setInterval(1);  connect(&timer,&QTimer::timeout,this,[this](){        static float count = 0;        count+= 0.01f;        global_i = std::fabs(sin(count));  this->update();  timer.setInterval(1);        timer.start();    });  
#endif  #if 0  timer.setInterval(1);  connect(&timer,&QTimer::timeout,this,[this](){        global_i+= 1;        if(fabs(global_i - 100) < 0.1f){            global_i = 0;        }        this->update();  timer.setInterval(1);        timer.start();    });  timer.start();#endif  }  MyGLWidget::~MyGLWidget()  {  makeCurrent();  glDeleteVertexArrays(1,&vertex_array_id);  glDeleteBuffers(1,&vertex_buffer_id);  doneCurrent();  
}  void MyGLWidget::initializeGL() {  initializeOpenGLFunctions();  glClearColor(0.2f,0.3f,0.3f,1.0f);  glGenVertexArrays(1,&vertex_array_id);  glBindVertexArray(vertex_array_id);  glGenBuffers(1,&vertex_buffer_id);  glBindBuffer(GL_ARRAY_BUFFER,vertex_buffer_id);  glBufferData(GL_ARRAY_BUFFER,sizeof(vertex_buffer_data),vertex_buffer_data,GL_STATIC_DRAW);  //启用layout = 0为当前绑定的VAO  glVertexAttribPointer(0,3,GL_FLOAT,GL_FALSE,0,nullptr);  glEnableVertexAttribArray(0);  //加载着色器  loadShader("/Users/liuhang/CLionProjects/opengl-learning/opengl1-3-matrix/shader/shader.vert",  "/Users/liuhang/CLionProjects/opengl-learning/opengl1-3-matrix/shader/shader.frag");  //    doTransform();  //解绑VAO  glBindVertexArray(0);  }  void MyGLWidget::paintGL() {  glClear(GL_COLOR_BUFFER_BIT);  glBindVertexArray(vertex_array_id);  //使用着色器程序  glUseProgram(shader_program_id);  //缩放  doTransform();  doMVP();  
#if 0  QMatrix4x4 scale_matrix = scaleMatrix(global_i,global_i,global_i);  QMatrix4x4 translate_matrix = translateMatrix(0.0,0.0,0.0);  QMatrix4x4 rotate_matrix = rotateMatrix(0.0f,0.0f,0.0f,0.0f);  QMatrix4x4 transform_matrix = translate_matrix * rotate_matrix * scale_matrix;    //获取uniform变量：transform_matrix，从着色器程序获取  uniform_transform_matrix_location = glGetUniformLocation(shader_program_id,"transform_matrix");  //上传uniform变量的4x4矩阵:transform_matrix，不需要转置,4fv结尾含义是4x4矩阵float类型,向量（vector）形式  glUniformMatrix4fv(uniform_transform_matrix_location,1,GL_FALSE,transform_matrix.data());  
#endif  glDrawArrays(GL_TRIANGLES,0,3);  
}  void MyGLWidget::resizeGL(int w, int h) {  glViewport(0, 0, w, h);  
}  void MyGLWidget::loadShader(std::string const& vertex_shader_path,std::string const& fragment_shader_path) {  //创建顶点着色器  vertex_shader_id = glCreateShader(GL_VERTEX_SHADER);  //读取shader.vert  std::string vertex_shader_code;  std::ifstream vertex_shader_stream(vertex_shader_path,std::ios::in);  if(vertex_shader_stream.is_open()){  std::stringstream ss;  ss << vertex_shader_stream.rdbuf();  vertex_shader_code = ss.str();  vertex_shader_stream.close();  }  else{  std::cout << "current path = " << std::filesystem::current_path() << std::endl;  if (!std::filesystem::exists(vertex_shader_path)) {  std::cerr << "File not found: " << vertex_shader_path << std::endl;  }  std::cerr << "read vertex_shader fail!" << std::endl;  return;  }  //加载vertex着色器程序代码  const char* vertex_shader_code_pointer = vertex_shader_code.c_str();  glShaderSource(vertex_shader_id,1,&vertex_shader_code_pointer,nullptr);  //编译vertex shader  glCompileShader(vertex_shader_id);  //查看vertex编译结果  GLint Result = GL_FALSE;  int infoLogLength;  glGetShaderiv(vertex_shader_id,GL_COMPILE_STATUS,&Result);  glGetShaderiv(vertex_shader_id,GL_INFO_LOG_LENGTH,&infoLogLength);  if(infoLogLength > 0){  std::vector<char> vertex_shader_error_message(infoLogLength+1);  glGetShaderInfoLog(vertex_shader_id, infoLogLength, nullptr, &vertex_shader_error_message[0]);  std::cout << "vertex shader:" << &vertex_shader_error_message[0] << std::endl;  }  //创建片段着色器  fragment_shader_id = glCreateShader(GL_FRAGMENT_SHADER);  //读取shader.frag  std::string fragment_shader_code;  std::ifstream fragment_shader_stream(fragment_shader_path,std::ios::in);  if(fragment_shader_stream.is_open()){  std::stringstream ss;  ss << fragment_shader_stream.rdbuf();  fragment_shader_code = ss.str();  fragment_shader_stream.close();  }  else{  std::cout << "current path = " << std::filesystem::current_path() << std::endl;  if (!std::filesystem::exists(vertex_shader_path)) {  std::cerr << "File not found: " << vertex_shader_path << std::endl;  }  std::cerr << "read fragment_shader fail!" << std::endl;  }  //加载fragment着色器程序代码  const char* fragment_shader_code_pointer = fragment_shader_code.c_str();  glShaderSource(fragment_shader_id,1,&fragment_shader_code_pointer,nullptr);  //编译fragment shader  glCompileShader(fragment_shader_id);  //查看fragment编译结果  glGetShaderiv(fragment_shader_id,GL_COMPILE_STATUS,&Result);  glGetShaderiv(fragment_shader_id,GL_INFO_LOG_LENGTH,&infoLogLength);  if(infoLogLength > 0){  std::vector<char> fragment_shader_error_message(infoLogLength+1);  glGetShaderInfoLog(fragment_shader_id, infoLogLength, nullptr, &fragment_shader_error_message[0]);  std::cout << "fragment shader compile error:" << &fragment_shader_error_message[0] << std::endl;  }  //创建着色器程序  shader_program_id = glCreateProgram();  //附加着色器到程序  glAttachShader(shader_program_id,vertex_shader_id);  glAttachShader(shader_program_id,fragment_shader_id);  //链接shader  glLinkProgram(shader_program_id);  //检查程序链接结果  glGetProgramiv(shader_program_id,GL_LINK_STATUS,&Result);  glGetProgramiv(shader_program_id,GL_INFO_LOG_LENGTH,&infoLogLength);  if(infoLogLength > 0){  std::vector<char>program_error_message(infoLogLength + 1);  glGetProgramInfoLog(shader_program_id,infoLogLength,nullptr,&program_error_message[0]);  std::cout << "program link:" << &program_error_message[0] << std::endl;  }  //删除着色器编译结果  glDeleteShader(vertex_shader_id);  glDeleteShader(fragment_shader_id);  
}  //平移x,y,z方向的大小  
QMatrix4x4 MyGLWidget::translateMatrix(float x, float y, float z)  
{  QMatrix4x4 translate_matrix;  translate_matrix.translate(x,y,z);  return translate_matrix;  
}  //缩放x,y,z的大小比例  
QMatrix4x4 MyGLWidget::scaleMatrix(float x, float y, float z) {  QMatrix4x4 scale_matrix;  scale_matrix.scale(x,y,z);  return scale_matrix;  
}  //默认逆时针angle，负数表示顺时针，绕(0,0,0)->(x,y,z)指向的方向旋转  
QMatrix4x4 MyGLWidget::rotateMatrix(float angle,float x,float y,float z) {  QMatrix4x4 rotate_matrix;  rotate_matrix.rotate(angle,x,y,z);  return rotate_matrix;  
}  void MyGLWidget::doTransform()  
{  QMatrix4x4 scale_matrix = scaleMatrix(1.0,1.0,0.0);  QMatrix4x4 translate_matrix = translateMatrix(0.0,0.0,0.0);  QMatrix4x4 rotate_matrix = rotateMatrix(0.0f,0.0f,0.0f,0.0f);  //叠加操作  QMatrix4x4 transform_matrix = translate_matrix * rotate_matrix * scale_matrix;  //获取uniform变量：transform_matrix，从着色器程序获取  uniform_transform_matrix_location = glGetUniformLocation(shader_program_id,"transform_matrix");  //上传uniform变量的4x4矩阵:transform_matrix，不需要转置,4fv结尾含义是4x4矩阵float类型,向量（vector）形式  glUniformMatrix4fv(uniform_transform_matrix_location,1,GL_FALSE,transform_matrix.data());  
}  void MyGLWidget::doMVP()  
{  //模型矩阵  QMatrix4x4 model_matrix;  model_matrix.setToIdentity();  //观察矩阵  QVector3D camera_pos = {4,4,3};  QVector3D look_dir = {1,0,0};  QVector3D up_dir = {0,1,0};  //lookAt  QMatrix4x4 view_matrix;  view_matrix.lookAt(camera_pos,look_dir,up_dir);  //投影矩阵  float angle = 45;  float aspect = this->width() * 1.0f / this->height();  //距离相机的位置，渲染范围：0.1-100  float near_plane = 0.1f;  float far_plane = 100.f;  QMatrix4x4 projection_matrix;  projection_matrix.perspective(angle,aspect,near_plane,far_plane);  //获取uniform变量  uniform_model_matrix_location = glGetUniformLocation(shader_program_id,"model_matrix");  uniform_view_matrix_location = glGetUniformLocation(shader_program_id,"view_matrix");  uniform_projection_matrix_location = glGetUniformLocation(shader_program_id,"projection_matrix");  //矩阵传入shader  glUniformMatrix4fv(uniform_model_matrix_location,1,GL_FALSE,model_matrix.data());  glUniformMatrix4fv(uniform_view_matrix_location,1,GL_FALSE,view_matrix.data());  glUniformMatrix4fv(uniform_projection_matrix_location,1,GL_FALSE,projection_matrix.data());  }

shader.vert

#version 330 core  layout(location = 0) in vec3 vertexPosion_modelspace;  
uniform mat4 transform_matrix;  uniform mat4 model_matrix;  
uniform mat4 view_matrix;  
uniform mat4 projection_matrix;  void main(){  mat4 MVP_matrix = projection_matrix * view_matrix * model_matrix;  gl_Position = MVP_matrix * transform_matrix * vec4(vertexPosion_modelspace,1.0);  
}

shader.frag

#version 330 core  out vec3 fragment_color;  void main(){  fragment_color = vec3(1.0,0.0,0.0);  
}