450. 删除二叉搜索树中的节点
目录
题目链接:
题目:
解题思路:
代码:
总结:
题目链接:
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
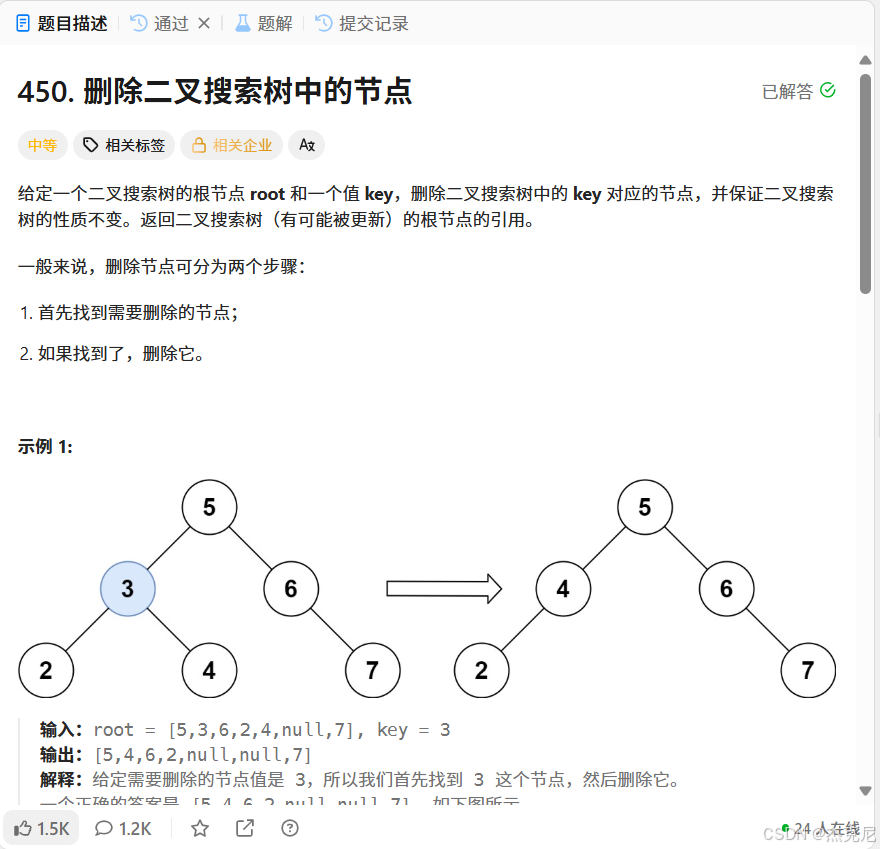
题目:
解题思路:
五种请情况:1未找到目标值,节点返回null
2目标值节点的左右子节点都为null,返回null
3目标值节点的左子树为null,返回右子树
4目标值节点的右子树为null,返回左子树
5都不为空,那就将左子树放在右子树的最左下面
代码:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode root, int key) {if(root==null) return root;if(root.val==key){if(root.left==null&&root.right==null) return null;else if(root.left!=null&&root.right==null) return root.left;else if(root.left==null&&root.right!=null) return root.right;else{TreeNode node=root.right;while(node.left!=null) node=node.left;node.left=root.left;return root.right;}}else if(root.val<key){root.right=deleteNode(root.right,key);}else{root.left=deleteNode(root.left,key);}return root;}
}二叉搜索树节点删除操作深度解析在二叉搜索树(Binary Search Tree,BST)的各类操作中,删除节点是相对复杂但又十分关键的操作。与插入和查找相比,删除需要考虑更多的情况,以确保删除节点后仍能维持二叉搜索树的特性。本文将对一段用于删除二叉搜索树中指定值节点的代码进行详细解析,带你深入理解其原理、执行流程及背后的逻辑。二叉搜索树删除节点的背景二叉搜索树的删除操作之所以复杂,是因为被删除的节点可能处于不同的位置,并且有不同的子节点情况。根据被删除节点的子节点数量,主要分为以下几种情况:被删除节点没有子节点(叶子节点):直接删除该节点即可。被删除节点只有一个子节点(左子节点或右子节点):用其子节点替代该节点的位置。被删除节点有两个子节点:需要找到一个合适的替代节点(通常是该节点右子树中的最小节点或左子树中的最大节点),将替代节点的值复制到当前节点,然后删除替代节点。代码整体结构java运行/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root==null) return root;
if(root.val==key){
if(root.left==null&&root.right==null) return null;
else if(root.left!=null&&root.right==null) return root.left;
else if(root.left==null&&root.right!=null) return root.right;
else{
TreeNode node=root.right;
while(node.left!=null) node=node.left;
node.left=root.left;
return root.right;
}
}else if(root.val<key){
root.right=deleteNode(root.right,key);
}else{
root.left=deleteNode(root.left,key);
}
return root;
}
}
这段代码的核心是 deleteNode 方法,它接收二叉搜索树的根节点 root 和要删除的节点值 key,并返回删除节点后的二叉搜索树的根节点。关键代码逐行解析处理空树情况java运行if(root==null) return root;
这是递归的终止条件之一。如果当前根节点 root 为 null,说明树为空或者已经遍历到了空的位置,直接返回 root(即 null)。找到要删除的节点java运行if(root.val==key){
// 处理不同子节点情况的代码
}
当当前根节点 root 的值等于要删除的 key 时,说明找到了要删除的节点,进入节点删除的处理逻辑。处理不同子节点情况叶子节点(没有子节点)java运行if(root.left==null&&root.right==null) return null;
如果要删除的节点是叶子节点(左子节点和右子节点都为 null),直接返回 null。这相当于将该节点从树中删除,因为其父节点的对应子节点引用会被更新为 null。只有左子节点java运行else if(root.left!=null&&root.right==null) return root.left;
如果要删除的节点只有左子节点,没有右子节点,那么返回其左子节点。这样,该节点的左子节点就会替代该节点的位置,维持二叉搜索树的结构。只有右子节点java运行else if(root.left==null&&root.right!=null) return root.right;
如果要删除的节点只有右子节点,没有左子节点,返回其右子节点,让右子节点替代该节点的位置。有两个子节点java运行else{
TreeNode node=root.right;
while(node.left!=null) node=node.left;
node.left=root.left;
return root.right;
}
如果要删除的节点有两个子节点,处理逻辑相对复杂:首先,找到该节点右子树中的最小节点(因为二叉搜索树右子树中的最小节点是大于当前节点值的最小元素,符合二叉搜索树的特性)。通过循环 while(node.left!=null) node=node.left; 来找到右子树中的最左节点,也就是最小节点。然后,将当前节点的左子树连接到找到的最小节点的左子节点上(node.left=root.left;)。最后,返回当前节点的右子节点,这样就用右子树中的最小节点替代了被删除的节点(因为最小节点的值已经通过后续的连接等操作间接起到了替代作用,而原来的右子节点成为新的子树结构的一部分)。递归查找要删除的节点java运行else if(root.val<key){
root.right=deleteNode(root.right,key);
}
如果当前根节点 root 的值小于要删除的 key,根据二叉搜索树的特性,要删除的节点应该在右子树中。所以,递归调用 deleteNode 方法,参数为 root.right(当前根节点的右子节点)和 key,并将返回的结果赋值给 root.right。这样,在右子树中找到并删除指定节点后,更新当前根节点的右子节点引用。java运行else{
root.left=deleteNode(root.left,key);
}
如果当前根节点 root 的值大于要删除的 key,同理,要删除的节点在左子树中。递归调用 deleteNode 方法,参数为 root.left 和 key,并将返回的结果赋值给 root.left,完成左子树中节点的查找和删除以及引用更新。返回根节点java运行return root;
在完成右子树或左子树的删除操作后,返回当前的根节点 root。这保证了每一层的根节点都能正确地将子树的引用传递给上一层,维护整个二叉搜索树的结构完整性。算法执行流程示例为了更好地理解代码的执行过程,我们通过一个具体的例子来模拟删除操作。假设初始的二叉搜索树结构如下(根节点值为 5,左子节点为 3,右子节点为 7;3 的左子节点为 2,右子节点为 4;7 的左子节点为 6,右子节点为 8):plaintext 5
/ \
3 7
/ \ / \
2 4 6 8
现在要删除值为 5 的节点(该节点有两个子节点)。调用 deleteNode(root, 5),其中 root 是值为 5 的节点。因为 root.val == key(5 == 5),进入有两个子节点的处理逻辑。找到右子树(值为 7 的节点)中的最小节点:从 7 开始,其左子节点是 6,6 没有左子节点,所以最小节点是 6。将当前节点(值为 5)的左子树(以 3 为根的子树)连接到最小节点 6 的左子节点上(node.left = root.left,此时 6 的左子节点变为以 3 为根的子树)。返回当前节点的右子节点(值为 7 的节点),作为新的根节点。最终,二叉搜索树的结构变为:plaintext 7
/ \
6 8
/
3
/ \
2 4
时间复杂度与空间复杂度时间复杂度该算法的时间复杂度为 \(O(h)\),其中 h 是二叉搜索树的高度。在理想情况下,二叉搜索树是平衡的,高度 \(h = \log n\)(n 为节点数),此时时间复杂度为 \(O(\log n)\)。但在最坏情况下,二叉搜索树可能退化为链表,此时高度 \(h = n\),时间复杂度为 \(O(n)\)。空间复杂度空间复杂度为 \(O(h)\),主要是由递归调用栈的深度决定的。递归调用的深度最多为二叉搜索树的高度 h,所以在理想情况下空间复杂度为 \(O(\log n)\),最坏情况下为 \(O(n)\)。总结这段用于删除二叉搜索树中指定值节点的代码,充分考虑了被删除节点的不同子节点情况,通过递归的方式,在找到要删除的节点后,根据其具体情况进行相应的处理,以维持二叉搜索树的特性。其核心思想是:利用二叉搜索树的特性递归查找要删除的节点,找到后根据子节点数量进行不同的删除和结构调整操作。理解这段代码,不仅有助于掌握二叉搜索树的删除操作,也能加深对递归算法和二叉搜索树特性的理解,为后续学习更复杂的树结构和操作(如平衡二叉树的调整)打下基础。
总结:
本文详细解析了二叉搜索树删除节点的操作,重点分析了五种不同情况的处理逻辑:空节点、叶子节点、单左/右子树节点、双子树节点。通过递归实现,代码将目标节点的左子树连接到右子树的最小节点下方,确保删除后仍保持BST特性。算法时间复杂度为O(h),空间复杂度为O(h),其中h为树高。该实现展现了BST删除操作的核心思想,为理解更复杂的树结构操作奠定了基础。
