当前位置：首页 > news >正文

【硬件-笔试面试题-102】硬件/电子工程师，笔试面试题（知识点：RC滤波器的参数怎么计算）

news 2025/9/20 15:48:05

题目汇总版--链接：

【硬件-笔试面试题】硬件/电子工程师，笔试面试题汇总版，持续更新学习，加油！！！-CSDN博客

1、题目

RC滤波器的参数怎么计算

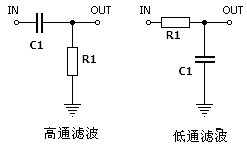
2、知识点

RC 滤波器是由电阻（R）和电容（C）组成的简单滤波电路，广泛应用于信号处理、电源去噪等场景。其参数计算核心是根据截止频率和阻抗匹配需求，确定电阻和电容的数值。以下按不同类型的 RC 滤波器详细说明计算方法：

一、RC 低通滤波器（最常用）

RC 低通滤波器允许低频信号通过，衰减高频信号（如过滤电源中的高频纹波）。

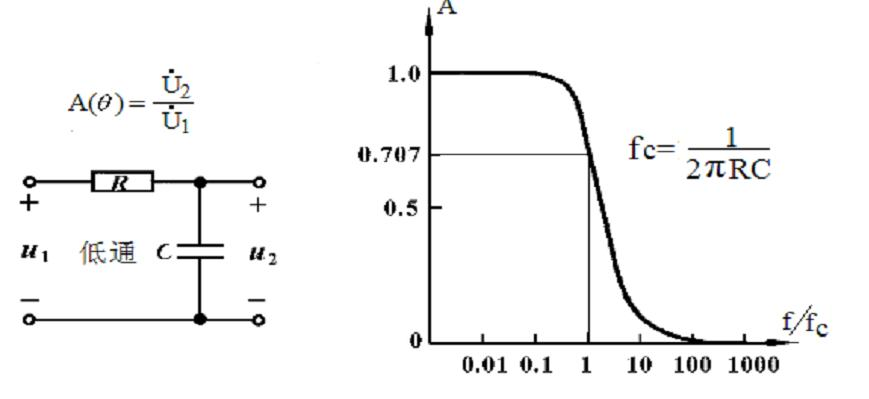
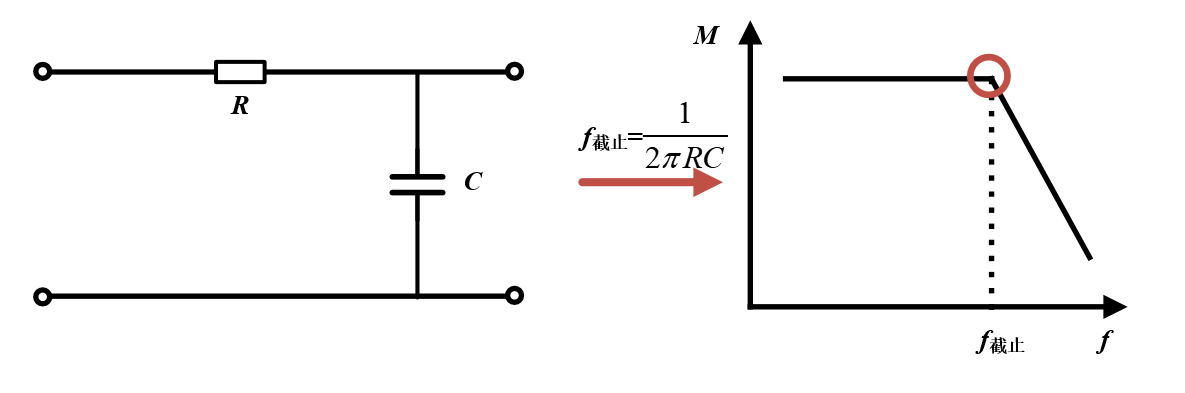
1. 一阶 RC 低通滤波器

电路结构：输入信号串联电阻 R，再并联电容 C 到地，输出取自电容两端。
核心参数：截止频率（\(f_c\)） 截止频率是信号幅度衰减 3dB（约 70.7%）的频率，计算公式：\(f_c = \frac{1}{2\pi R C}\) 其中：
- \(f_c\)：截止频率（单位：Hz）
- R：电阻值（单位：Ω）
- C：电容值（单位：F）
参数计算步骤： ① 确定需要保留的最高频率（通常取截止频率\(f_c\)略高于该频率）； ② 先选定电阻 R（根据电路阻抗匹配需求，如信号源输出阻抗为 50Ω，可选 R=50Ω）； ③ 根据截止频率公式反推电容 C：\(C = \frac{1}{2\pi R f_c}\)

示例：设计一个截止频率为 1kHz 的低通滤波器，选 R=10kΩ，则：\(C = \frac{1}{2\pi \times 10^4 \times 10^3} \approx 15.9nF \quad (\text{实际可选16nF标准值})\)

二、RC 高通滤波器

RC 高通滤波器允许高频信号通过，衰减低频信号（如去除直流分量，保留交流信号）。

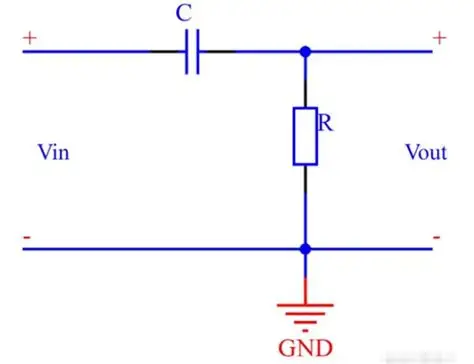
1. 一阶 RC 高通滤波器

电路结构：输入信号串联电容 C，再并联电阻 R 到地，输出取自电阻两端。
核心参数：截止频率（\(f_c\)） 与低通滤波器公式相同（物理意义相反：低于\(f_c\)的信号被衰减）：\(f_c = \frac{1}{2\pi R C}\)
参数计算步骤： ① 确定需要抑制的最高低频信号（如 50Hz 工频干扰），截止频率\(f_c\)应高于该频率； ② 选定电容 C（根据信号频率和容抗，高频信号需小电容，如 100nF）； ③ 反推电阻 R：\(R = \frac{1}{2\pi C f_c}\)

示例：设计一个抑制 50Hz 工频干扰的高通滤波器，选\(f_c=100Hz\)，C=100nF，则：\(R = \frac{1}{2\pi \times 100 \times 10^{-9} \times 100} \approx 15.9kΩ \quad (\text{实际可选16kΩ标准值})\)

三、RC 带通滤波器

RC 带通滤波器允许特定频率范围的信号通过（如音频中的特定频段），通常由高通 + 低通滤波器串联组成。

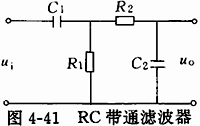
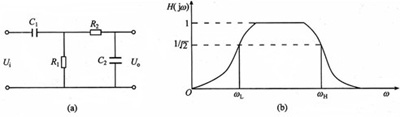
1. 二阶 RC 带通滤波器

电路结构：输入→高通 RC（\(R_1, C_1\)）→低通 RC（\(R_2, C_2\)）→输出。
核心参数：
- 低截止频率（高通部分）：\(f_{c1} = \frac{1}{2\pi R_1 C_1}\)
- 高截止频率（低通部分）：\(f_{c2} = \frac{1}{2\pi R_2 C_2}\)
- 带宽：\(BW = f_{c2} - f_{c1}\)（需满足\(f_{c2} > f_{c1}\)）
参数计算步骤： ① 确定需要保留的频率范围（如 1kHz~10kHz），即\(f_{c1}=1kHz\)，\(f_{c2}=10kHz\)； ② 分别计算高通和低通的 R、C 值（通常取\(R_1=R_2=R\)简化设计）：
- 高通：选 R=10kΩ，则\(C_1 = \frac{1}{2\pi \times 10^4 \times 10^3} \approx 15.9nF\)
- 低通：同 R=10kΩ，则\(C_2 = \frac{1}{2\pi \times 10^4 \times 10^4} \approx 1.59nF\)

四、RC 带阻滤波器（陷波滤波器）

RC 带阻滤波器抑制特定频率（如 50Hz/60Hz 工频干扰），允许其他频率通过，通常由高通 + 低通滤波器并联组成。

1. 二阶 RC 带阻滤波器

核心参数：抑制频率（中心频率）：\(f_0 = \frac{1}{2\pi R C}\) （与低通 / 高通公式相同，通过调整 R 和 C 使中心频率等于目标抑制频率）

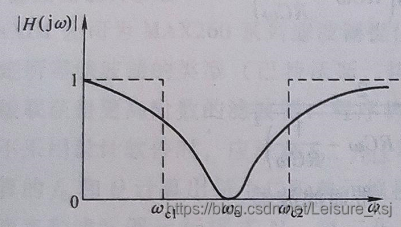
示例：设计一个抑制 50Hz 工频干扰的带阻滤波器，选 R=10kΩ，则：\(C = \frac{1}{2\pi \times 10^4 \times 50} \approx 318nF\)

五、关键设计考量

阻抗匹配：滤波器的输入 / 输出电阻应与前后级电路匹配（如信号源内阻 50Ω，选 R=50Ω），否则会导致信号反射和衰减特性偏移。
电容类型选择：
- 高频滤波（如 1MHz 以上）：选陶瓷电容（如 MLCC），等效串联电阻（ESR）低，响应速度快；
- 低频滤波（如 1kHz 以下）：选电解电容，容值大，适合滤除低频纹波。
负载影响：若负载阻抗较小（如 < 10kΩ），会分流电容电流，导致截止频率升高。解决方法：在滤波器与负载间加缓冲电路（如射极跟随器），提高输入阻抗。
多级滤波：单级 RC 滤波器高频衰减率为 - 20dB / 十倍频，若需更强衰减（如 - 40dB / 十倍频），可级联两级 RC 滤波器（注意级间阻抗匹配）。