速通ACM省铜第九天 赋源码（Divine Tree)
目录
引言：
Divine Tree
题意分析
逻辑梳理
错误思路分析
代码实现
结语：
引言：
今天我们来讲一道CF难度分为1400的题，这道题虽然是今天讲的，但其实这题我从昨天就开始想起来了，本来想昨天开掉顺便发在昨天的博客里的，但瓶颈了，没打出来，到今天晚上才打出来，所以今天就只能讲这一题了，那么，我们就进入今天的算法讲解——————>
Divine Tree
那按照惯例，我们先来看题目
题意分析
题目链接在这Problem - 2120C - Codeforces
不想跳转的可以看下图
题目很短啊，那么我们来看一下题目讲的什么
首先先输入俩个数，第一个数为节点的个数（节点编号从1到n）,第二个数是创造成的树按照一定方式计算需要达到的值
那树的值怎么计算呢，在树中先选择一个根作为起始，然后将每个点到根的那段路径中最小的值加起来要得到满足条件的值，说起来比较绕口，结合图来理解应该好理解点，如图
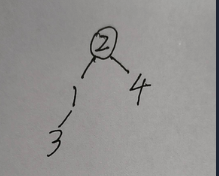在这个图中的树，根节点为2，那么这个树的值就是2+1+1+2=6（根节点自身也要算）
然后看能否构造出满足条件的树
若不可以就输出 -1
若可以就先输出构建完的树的根节点，然后再输出树的每条边即可
这就是这题目想表达的意思，接下来我们就进入逻辑梳理的阶段
逻辑梳理
首先，有ｎ个节点的树最小值是什么时候呢，就是根节点为１的时候，即树的值为ｎ．那最大值是什么时候呢，就是根节点为ｎ时，往下的节点依此比上一个节点小１，即链式结构，此时树的值最大，即为从１加到ｎ，用等差数列的运算公式表示就是（１＋ｎ）＊ｎ／２．
所以树创建完得到的值范围为ｎ到（１＋ｎ）＊ｎ／２，若想要得到的值不在这个范围之内，那么就直接输出－１就可以，若在范围内，就进行下一步操作。
在进行下一步操作前，有的人可能会想知道了树的最小值和最大值，那这俩个值之间的所有值都可以达到吗？
是的，都可以达到，而且都可以构造成链式结构，直接用链式结构来考虑是关键，若用树来考虑这题会很麻烦（至少我不会），首先最小值和最大值都是链式结构实现的，一个是单调递增的链式结构，一个是单调递减的链式结构，那么我们想要达到中间的任意值，只需要对顺序进行调整就可以了（这是关键，这个思路让我卡了很久）
进行树的构造的时候，千万不要先找到根，在进行操作，我一开始是往这个方向想的，导致代码一直一筹莫展（时间复杂度过高），为什么不行我会在逻辑梳理的最后面讲
正确的逻辑是怎么样的，应该是从前往后遍历，然后数据从大到小放进去，看是否满足条件，从１到ｎ的下标，分别放ｎ到１的数据，一直往下走，直到不满足条件为止，那什么时候算不满足条件呢
那便是前面的数据加起来后把后面剩余的数据都当１来看，加起来若大于需要的值了，则不满足条件了，为什么后面都可以当１来看呢，因为是从大到小放进去的数，所以１肯定是最后放，但也可以在前面数放完后放１，那么后面的所有数都变成了１，这个时候便是在前面数据确定的情况下，能构建的最小的树了，若不满足，自然就不能放剩余数里的最大值了
这个时候，我们可以怎么办呢，我看了挺多的题解，好想都没有我这种方法，但代码量是挺少的，而且肯定保真，想要验证这个结论的正确性，你们自己想一下也是很快就能想通的，我们只需要将剩余的值减去后面剩余位置当１处理时的值然后得到一个值，那个值便是当前位置需要放的值，然后直接跳出循环就好了，因为后面是从１开始的剩余元素
那么怎么记录剩余元素呢，我们可以用一个数组来标记，已经放过的元素就标记，然后从１开始遍历到ｎ，把没标记的元素放入数组就可以了
这便是正确的思路，那么我们来看为什么一开始的那个思路是错误的（有兴趣的可以看一下，也可以直接跳转代码实现看ＡＣ码）
错误思路分析
我一开始是想着链表先按１到ｎ排序，然后这个排序时候，最初时候树的值为ｎ，我那时候是想着是从前往后遍历，以每个下标为根节点，每次树的值的增加值为ｎ－上一个元素
然后直到遍历到大于需求值之后再对左边的部分进行操作，因为右边的元素的值都大于根，所以右边元素不管怎么变化值都是根节点的元素，右边可以通过换位来进行值的修正
但很明显，这种是完全不可能实现的，因为元素的数据范围为１０的６次，但是我们在第一次遍历寻找时就已经时间复杂度为Ｏ（ｎ）了，然后之后的操作还在这个循环内部，就算按照上面正确的思路方式对右边的元素进行操作也很可能会超时，毕竟嵌套了２层循环，最糟糕的情况便是ｎ方 的时间复杂度，所以这个思路是错误的
那么讲解完这些后，你们应该逻辑都已经清晰了，我们来看具体的代码实现
代码实现
具体的代码实现就没有什么好说的了，用vis数组来标记是否访问过元素，然后用vector数组来存数据就可以了，数据的变化就创建一个now变量来进行迭代判断即可
那么，接下来就来看AC源码吧
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <vector>
using namespace std;int t, ans;
bool vis[1000010];void solve()
{memset(vis, 0, sizeof(vis));long long n, m, now;cin >> n >> m;now = m;vector<int>a;if ((n + 1) * n / 2 < m || m < n){cout << "-1" << endl;return;}for (int i = 1; i <= n; i++){if (now - (n - i + 1) > n - i){now -= n - i + 1;vis[n - i + 1] = 1;a.push_back(n - i + 1);}else{ int l = now - (n - i);a.push_back(l);vis[l] = 1;break;}}for (int i = 1; i <= n; i++){if (!vis[i])a.push_back(i);}cout << a[0] << endl;for (int i = 0; i < a.size()-1; i++){cout << a[i] << " " << a[i + 1] << endl;}
}int main()
{cin >> t;while (t--){solve();}return 0;
}那么，这题就讲解完啦
结语：
今日算法讲解到此结束啦，希望对你们有所帮助，谢谢观看，如果觉得不错可以分享给朋友哟。当然也可以关注一下哦
