C语言 ——— 数组
目录
一维数组的创建和初始化
一维数组的创建
创建数组时 [ ] 使用变量创建
一维数组的初始化
一维数组的使用
下标引用操作符[]
一维数组在内存中的存储
二维数组的创建和初始化
二维数组的创建
二维数组的初始化
二维数组的使用
二维数组在内存中的存储
数组越界
规避越界方法
数组名是什么?
通常情况下数组名是首元素地址
两个例外
1. 数组名单独置于 sizeof() 内部时(即 sizeof(数组名))
2. 使用 & 取数组名地址时(即 &数组名)
数组作为函数参数
实现整型数组的冒泡排序(升序)
一维数组的创建和初始化
一维数组的创建
整型数组的创建:
int arr[10];
整型数组的定义遵循 类型名 数组名[元素个数] 的格式。以 int arr[10]; 为例:
int是数据类型关键字,表明数组中每个元素均为整型(占 4 字节,32 位系统下)。arr是数组的标识符(名称),用于在程序中唯一标识该数组,通过它可访问数组的内存空间。[10]表示数组的容量,即该数组在内存中连续分配的存储空间可容纳 10 个整型元素。
字符数组的创建:
char arr[10];
字符数组的定义采用 char 数组名[元素数量] 的形式。以 char arr[10]; 为例:
char作为数据类型关键字,指定数组中每个元素均为字符类型(通常占 1 字节 内存,可存储 ASCII 字符)。arr是数组的标识符(名称),用于在程序中唯一标识该数组,通过它可访问数组的内存空间。[10]表示数组的容量,即该数组在内存中 连续分配 的存储空间可容纳 10 个字符元素
创建数组时 [ ] 使用变量创建
代码演示:
int count = 10;
int arr[count];在 C 语言发展中,数组大小的定义规则与编译器支持存在阶段性差异:
C99 标准之前
数组的大小必须由编译时确定的常量(如字面量或宏定义)指定。若使用变量定义数组大小(如 int n; int arr[n];),编译器会报错,因为变量值在编译阶段无法确定,传统 C 语言需在编译期为数组分配固定内存空间。
C99 标准引入变长数组(VLA)
C99 允许数组大小在运行时由变量决定,例如根据用户输入的数值创建数组。但存在限制:
- 不可初始化:无法在定义时为数组元素赋初值(因大小未知)。
- 栈上动态分配:内存于栈区分配,随作用域结束自动释放,不同于
malloc等动态内存分配方式。
编译器支持差异
- VS2019/VS2022(MSVC 编译器):默认不支持 C99 变长数组,使用变量定义数组大小会触发编译错误,因微软编译器更侧重 C++ 兼容性及平台特性。
- GCC/Clang 等开源编译器:支持变长数组,需通过编译选项启用 C99 模式,更贴合 C 语言标准特性
一维数组的初始化
整型数组的初始化(完全初始化):
int arr[10] = { 1,2,3,4,5,6,7,8,9,10 };
arr 数组能存储 10 个整型的元素,而刚好初始化的时候赋值了 10 个元素,这就是完全初始化,需要注意的是,要是 arr 数组最多只能存储 10 个元素,但是初始化的时候存储超过了 10 个元素就会报错
整型数组的初始化(不完全初始化):
int arr[10] = { 1,2,3,4,5 };
同样这个 arr 数组能存储 10 个整型元素,只初始化了 5 个元素,那么剩余的 5 个元素会自动初始化为 0
整型数组的初始化(全 0 初始化):
int arr[10] = { 0 };
只初始化了一个 0 ,那么剩下的元素也全都是初始化为 0
整型数组的初始化(根据初始化的元素个数来确定数组的大小):
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
在 [] 中没有给定 arr 数组的空间,但是在初始化的时候给定了是初始化 10 个元素,那么数组的大小就会根据初始化的个数来确定,也就是 10 个整型元素的总大小
字符数组的初始化:
char arr1[] = "abcd";char arr2[] = { 'a','b','c','d' };
arr1 字符数组的大小会根据初始化的字符串长度来确定,并且字符串结尾有一个隐藏的字符串结束标志 '\0' , 所以 arr 字符数组的大小是 5 个字节
而 arr2 字符数组的大小不能确定,因为 arr2 数组只存放了 4 个字符,并没有手动存放 '\0' 字符,所以用 strlen 计算 arr2 数组大小的时候会是随机值
通过监视的角度验证: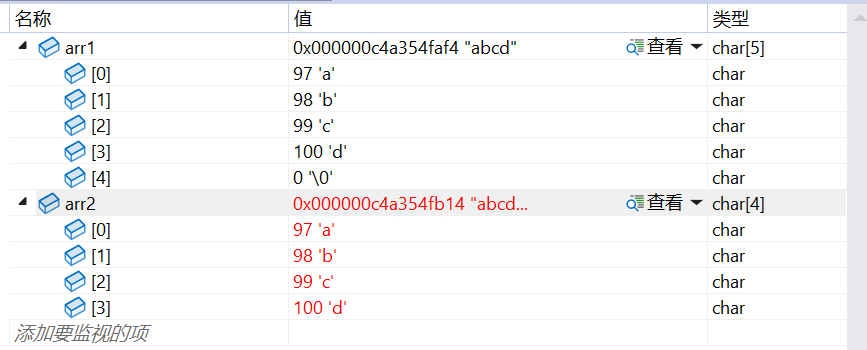
一维数组的使用
下标引用操作符[]
在一维数组的操作中,下标引用操作符[] 是访问数组元素的关键工具,其核心作用是通过指定下标,精准定位并访问数组中的每一个元素。
代码演示:
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
- 数组大小:
arr数组的大小由花括号内的元素数量决定,共包含 10 个元素。由于每个整型元素占用 4 字节,因此arr数组的总字节数为 10×4=40 字节。 - 下标规则:C 语言规定数组元素的下标从 0 开始,从左至右依次递增 1。在
arr数组中,元素1的下标为 0,元素2的下标为 1,以此类推,直到元素10的下标为 9。
那么想要访问 arr 数组中的每个元素,就是通过 下标引用操作符[] 来访问。
代码演示(单个元素的访问):
printf("%d\n", arr[3]); //4
printf("%d\n", arr[7]); //8代码演示(整个元素的访问):
int sz = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < sz; i++)
{printf("%d ", arr[i]);
}在代码片段中,int sz = sizeof(arr) / sizeof(arr[0]); 用于计算数组 arr 的元素总数:
sizeof(arr)表示整个数组占用的总字节数;sizeof(arr[0])表示数组中单个元素(此处为第一个元素)的字节数;- 两者相除的结果即为数组包含的元素个数,存储在变量
sz中。
后续通过 for 循环遍历数组并打印元素:
循环变量 i 从 0 开始,直到 i < sz 时终止(即最大取值为 sz-1),恰好覆盖了数组从第一个元素(下标 0)到最后一个元素(下标 sz-1)的所有合法下标。通过 arr[i] 访问对应下标元素并打印,最终实现数组所有元素从左到右的依次输出。
一维数组在内存中的存储
若需了解一维数组各元素在内存中的存储布局,可借助 printf 函数中的 %p 格式说明符 —— 其核心用途是打印数据在内存中的地址,通过该格式符能直观获取数组每个元素的内存地址,进而分析存储布局。
代码演示:
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };int sz = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < sz; i++)
{printf("&arr[%d] = %p\n", i, &arr[i]);
}数组元素地址的打印方式
- 对于包含 1 到 10 这 10 个元素的 int 类型数组 arr,若要打印每个元素的地址,需先计算数组的元素总数,存储在变量 sz 中。
- 接着通过 for 循环遍历数组,循环变量 i 从 0 开始,直到 i 小于 sz 时结束,以此覆盖数组所有元素的合法下标。
for 循环中 printf 函数的作用
- 循环体内的 printf 函数用于格式化输出元素地址,具体解析如下:
- 格式控制字符串为
"&arr[%d] = %p\n",其中%d以十进制形式输出当前循环变量 i 的值(即元素下标),%p以标准地址格式输出对应元素的内存地址; - 参数 i 为
%d提供具体的下标数值,&arr[i](&是取地址运算符)为%p提供该下标对应元素的内存地址; - 最终会按
"&arr[下标] = 地址值"的格式逐行打印,清晰呈现每个元素在内存中的位置。
- 格式控制字符串为
代码验证: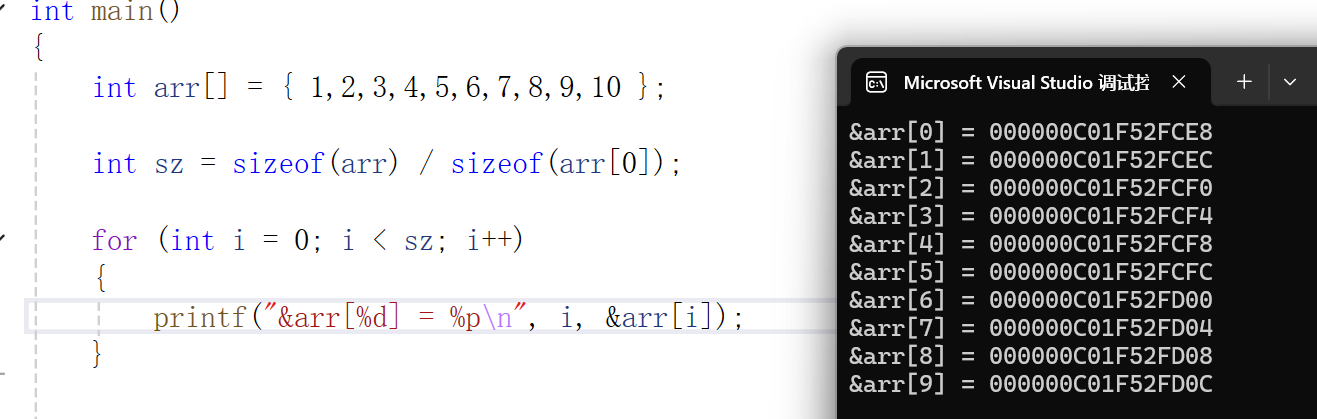
由此可见,由于 arr 数组的元素类型为 int,其每个元素在内存中占用 4 个字节,因此数组元素从左到右在内存中的存储地址依次递增 4 个字节。
同时也能明确,一维数组的所有元素在内存中呈现为连续排列的存储状态,不存在地址间隔。
二维数组的创建和初始化
二维数组的创建
代码演示:
int arr[3][4];
通过 int arr[3][4] 这样的形式定义后,arr 就成为了一个二维数组。
其中方括号内的两个数字含义明确:第一个数字 3 代表该二维数组包含 3 行,即数组在纵向被划分为 3 个独立的元素组;第二个数字 4 有两层核心含义,一是代表数组的每一行都包含 4 个元素,二是从列的维度来看,它也等同于数组拥有 4 列,即数组在横向方向上,每一行的元素数量统一为 4 个。
从内存逻辑来看,这样的定义让二维数组的结构更清晰 —— 可以将其理解为 “包含 3 个一维数组的数组”,而这 3 个一维数组又各自包含 4 个 int 类型元素,这种 “行 - 列” 的划分方式,也让后续通过行号和列号定位具体元素(如 arr [0][1])变得直观且不易出错。
二维数组的初始化
完全初始化:
int arr[3][4] = { {1,2,3,4},{2,3,4,5},{3,4,5,6} };
对于定义语句 int arr[3][4] 这个二维数组,其初始化数据的结构与二维数组的 “行 - 列” 逻辑完全对应:
- 大括号内的第一个子括号 {1,2,3,4},对应数组的第一行元素,其中包含 4 个数值,恰好匹配了数组定义时指定的 “4 列” 规则;
- 第二个子括号 {2,3,4,5} 对应数组的第二行元素,第三个子括号 {3,4,5,6} 对应数组的第三行元素,二者同样各自包含 4 个数值,与 “4 列” 的设定保持一致。
若将这个二维数组想象成一个有序的空间:
1,2,3,4
2,3,4,5
3,4,5,6
其元素访问规则可类比一维数组,但需通过 “行下标 + 列下标” 双重定位:
- 二维数组的下标同样从 0 开始计数,行下标对应 “第几行”,列下标对应 “第几列”;
- 若要访问第一个元素 1,它位于 “第 1 行第 1 列”,对应下标就是 arr[0][0];
- 同理,若要访问第二行中的元素 4,该元素在第二行(行下标 1)的第三个位置(列下标 2),因此访问方式为 arr[1][2]。
不完全初始化:
int arrA[3][4] = { 1,2,3,4,2,3,4,5,3,4,5,6 };int arrB[3][4] = { {1},{2,3},{3,4,5} };针对:arrA[3][4]
该数组初始化时,大括号内未嵌套子括号,仅给出一串连续的数值。此时编译器会依据数组定义时指定的 “每一行有 4 个元素”(即 [4] 所代表的列数)来自动分配数值:
- 从第一个数值开始,每 4 个数值自动归为一行,依次填充数组的第一行、第二行、第三行;
- 由于给出的数值总数(12 个)恰好等于数组总元素数(3 行 × 4 列 = 12 个),最终会完整填充整个数组,无需额外补值,相当于完成了 “隐式按行排序” 的初始化。
针对:arrB[3][4]
该数组初始化时,大括号内嵌套了与行数(3 行)对应的 3 个小括号,但每个小括号内的初始化数值都未填满 “每一行 4 个元素” 的要求。这种情况下,编译器会对每个小括号内未明确初始化的元素自动补全为 0:
- 第一个小括号
{1}对应第一行,仅初始化了第 1 个元素,剩余 3 个元素补 0,最终第一行元素为{1,0,0,0}; - 第二个小括号
{2,3}对应第二行,仅初始化了前 2 个元素,剩余 2 个元素补 0,最终第二行元素为{2,3,0,0}; - 第三个小括号
{3,4,5}对应第三行,仅初始化了前 3 个元素,剩余 1 个元素补 0,最终第三行元素为{3,4,5,0}。
不完全初始化(省略行):
int arr[][4] = { 1,2,3,4,2,3,4,5,3,4,5,6 };
其核心特点在于二维数组初始化时的 “行可省、列不可省” 规则:
-
行的省略与自动判断:
该数组定义时,第一个方括号(代表行数)为空,仅指定了第二个方括号的 4(代表列数)。此时编译器会自动计算行数:它会先根据 “每一行有 4 个元素”(由[4]确定)的规则,对初始化列表中的所有数值(共 12 个)进行分组,每 4 个数值归为一行,最终自动判断出数组共有 3 行,并完成初始化。 -
列不能省略的原因:
初始化二维数组时,列数绝对不能省略。因为列数直接决定了 “每一行应该包含多少个元素”,是编译器对初始化数值进行分组、确定行数的核心依据。若省略列数,编译器无法判断数值应如何划分到不同行中,也就无法完成数组的正确初始化。
综上,二维数组初始化的关键规则是:仅允许省略代表行数的第一个方括号,代表列数的第二个方括号必须明确指定。
二维数组的使用
要访问二维数组中的任意一个元素,同样需要使用 下标引用操作符 [],但与一维数组仅需一个下标定位不同:
访问二维数组的单个元素时,必须通过两个下标共同确定位置 —— 第一个下标用于指定元素所在的 “行”,第二个下标用于指定元素所在的 “列”,只有同时明确行和列的位置,才能精准定位并访问到目标元素。
代码演示:
int arr[3][4] = { {1,2,3,4},{2,3,4,5},{3,4,5,6} };int row = sizeof(arr) / sizeof(arr[0]); //行
int col = sizeof(arr[0]) / sizeof(arr[0][0]); //列for (int i = 0; i < row; i++)
{for (int j = 0; j < col; j++){printf("%d ", arr[i][j]);}printf("\n"); //换行
}要通过下标打印 arr[3][4] 数组的所有元素,核心步骤是先通过 sizeof 运算符计算出数组的行数和列数,再用双重循环遍历并打印,具体逻辑如下:
一、计算数组的行数(row)
- 核心原理:行数 = 数组总字节大小 ÷ 每一行的字节大小。
- 具体计算:
sizeof(arr):用于获取整个二维数组的总字节大小。由于数组是int类型(每个int占 4 字节),共 3 行 4 列(12 个元素),因此总大小为 12 × 4 = 48 字节。sizeof(arr[0]):用于获取数组第一行的字节大小。因为二维数组的每一行结构完全相同(均为 4 个int元素),所以第一行的大小可代表所有行的大小,计算结果为 4 × 4 = 16 字节。- 因此,
sizeof(arr) / sizeof(arr[0])即 “48 字节 ÷ 16 字节”,最终得出数组共有 3 行,并将结果存入变量row。
二、计算数组的列数(col)
- 核心原理:列数 = 某一行的总字节大小 ÷ 单个元素的字节大小。
- 具体计算:
sizeof(arr[0][0]):用于获取数组中单个元素的字节大小。因数组元素类型为int,所以每个元素固定占 4 字节。- 结合前文已知
sizeof(arr[0]) = 16 字节(第一行大小),因此sizeof(arr[0]) / sizeof(arr[0][0])即 “16 字节 ÷ 4 字节”,最终得出数组共有 4 列,并将结果存入变量col。
这种通过 sizeof 计算行列数的方式,无需手动硬编码行数和列数,即使后续修改数组的初始化数据或大小,代码也能自动适配,灵活性更高。
三、通过双重循环打印所有元素
计算出 row(3 行)和 col(4 列)后,就可以用双重 for 循环遍历数组:
- 外层循环控制 “行”:循环变量
i从 0 开始,到i < row结束,依次定位每一行(如i=0对应第一行,i=1对应第二行)。 - 内层循环控制 “列”:循环变量
j从 0 开始,到j < col结束,依次定位当前行中的每一列(如j=0对应第一列,j=1对应第二列)。 - 循环体内通过
arr[i][j]精准定位 “第i行第j列” 的元素,再用printf打印;当内层循环结束(即打印完一行所有元素)后,通过printf("\n")换行,最终让打印结果按 “行 - 列” 格式整齐呈现。
二维数组在内存中的存储
查看二维数组在内存中的存储方式,与查看一维数组的方法类似:只需将数组中所有元素的地址按顺序从左到右依次打印出来,就能清晰呈现其存储特性。
代码演示:
int arr[3][4] = { {1,2,3,4},{2,3,4,5},{3,4,5,6} };int row = sizeof(arr) / sizeof(arr[0]); //行
int col = sizeof(arr[0]) / sizeof(arr[0][0]); //列for (int i = 0; i < row; i++)
{for (int j = 0; j < col; j++){printf("&arr[%d][%d] = %p\n", i, j, &arr[i][j]);}printf("\n"); //换行
}代码验证: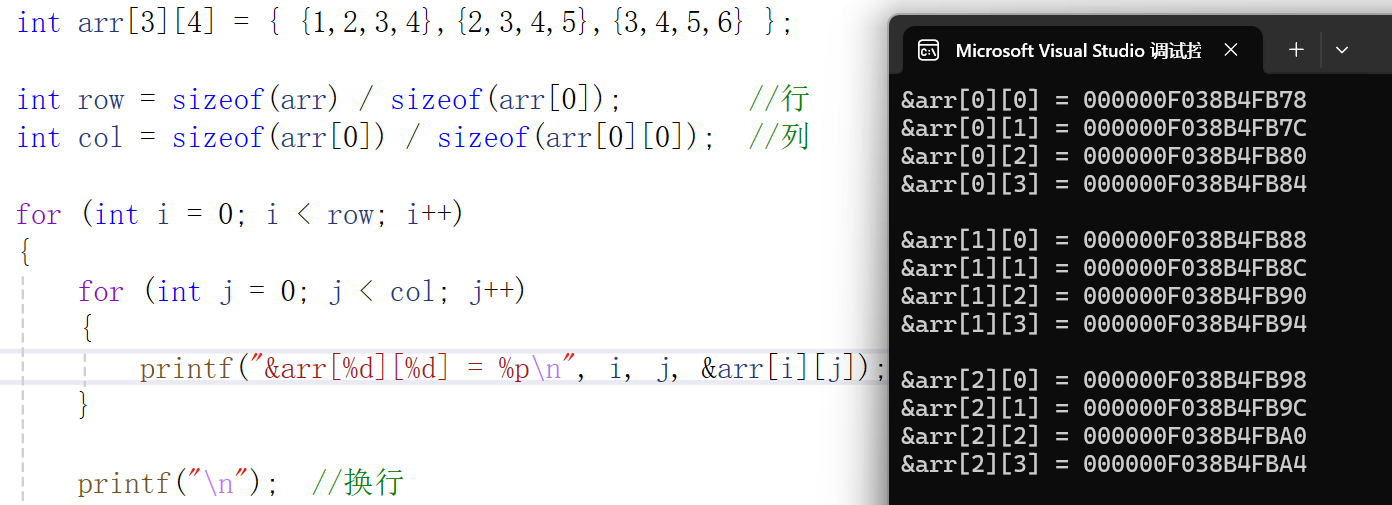
通过查看二维数组元素的内存地址可明确:其存储方式与一维数组完全一致,并非以我们直观想象的 “行 - 列二维空间” 形式存放,而是将数组中所有元素在内存中按顺序连续排列。
具体来说,二维数组会先完整存储第一行的所有元素,第一行元素存储结束后,紧接着连续存储第二行的所有元素,后续行以此类推,整个数组的元素在内存中不存在地址间隔,呈现出和一维数组相同的 “线性连续” 存储特征。
数组越界
数组的下标存在明确的范围边界,且所有数组的下标均从 0 开始计数,这是数组访问的基础规则。
以一维数组 arr 为例,若该数组共有 n 个元素,那么其下标范围会严格限定在 0 到 n-1 之间 —— 其中 0 对应数组的第一个元素,n-1 则对应数组的最后一个元素。
一旦访问数组时使用的下标超出 n-1(比如用 n 或更大的数值作为下标),就会触发数组越界访问。这种操作本质上是在访问数组定义范围之外的内存空间,而这部分空间可能存储着其他变量的数据或系统信息,不仅会导致程序读取到错误的数值、输出混乱结果,严重时还可能破坏其他数据,甚至引发程序崩溃。需要特别注意的是,许多编程语言(如 C 语言)不会对数组越界做强制检查,因此开发者需主动确保下标在合法范围内,避免这类隐患。
代码演示:
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
从 arr 数组包含 10 个元素这一前提可明确,该数组的下标存在严格的合法范围,即从 0 到 9—— 其中下标 0 对应数组的第一个元素,下标 9 对应数组的最后一个元素。
因此,在访问该数组时,无论出现两种情况中的哪一种,都属于非法访问:
- 下标数值小于 0(如使用 -1、-2 等作为下标);
- 下标数值大于 9(如使用 10、11 等作为下标)。
这类非法访问会越过数组的内存边界,可能导致读取错误数据、破坏其他变量,甚至引发程序崩溃,需格外注意规避。
规避越界方法
int sz = sizeof(arr) / sizeof(arr[0]); //数组元素个数int left = 0; //左下标
int right = sz - 1; //右下标在定义好数组 arr 后,首先计算出数组的元素总个数 sz。在此基础上,进一步定义两个关键变量:int left = 0;(代表数组的左下标,即第一个元素的下标)和 int right = sz - 1;(代表数组的右下标,即最后一个元素的下标)。
后续在访问或修改数组元素时,始终以这三个变量作为参照:确保使用的下标在 left 到 right 的范围内(包括边界值)。这种方式能从逻辑上约束对数组的操作,避免因手动输入固定下标(如直接写 5 或 10)而可能出现的越界风险,从而有效降低甚至规避数组越界问题。
这种方法的优势在于,即使后续数组的大小发生变化,只需重新计算 sz,left 和 right 也会自动适配新的数组范围,无需手动调整,大大提升了代码的健壮性和可维护性。
数组名是什么?
通常情况下数组名是首元素地址
在多数场景下,数组名的本质就是数组首元素的内存地址,而非数组本身或数组的全部内容。
代码演示:
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };printf("%p\n", arr);
printf("%p\n", arr[0]);打印 arr 数组名的地址和打印 arr[0] 第一个元素的地址是相同的
代码验证:
两个例外
尽管 “数组名通常代表首元素地址” 是核心规则,但存在两个关键例外场景,此时数组名的含义会发生变化:
1. 数组名单独置于 sizeof() 内部时(即 sizeof(数组名))
这种情况下,数组名代表的是整个数组,而非首元素地址。因此 sizeof(数组名) 计算的是整个数组所占的总字节大小,结果等于 “数组元素个数 × 单个元素的字节大小”。
代码演示:
int arr[5] = { 1,2,3,4,5 };printf("sizeof(arr) = %d\n", sizeof(arr)); //20byte
int arr[5] 的 sizeof(arr) 结果为 5×4=20 字节( int 占 4 字节),而非单个元素地址的大小(通常为 4 或 8 字节,取决于系统位数)。这一例外是为了方便开发者直接获取数组的整体内存占用,无需手动计算元素个数再相乘。
2. 使用 & 取数组名地址时(即 &数组名)
这里取出的并非数组首元素的地址,而是整个数组的地址。从数值上看,“整个数组的地址” 与 “首元素的地址” 是相同的(都指向数组在内存中的起始位置),但二者的 “地址类型” 完全不同:
代码演示:
int arr[5] = { 1,2,3,4,5 };printf("%p\n", arr + 1); //跳过一个元素的大小
printf("%p\n", &arr + 1); //跳过整个数组的大小- “首元素地址” 的类型是 “单个元素的指针类型”(如
int*),对其进行+1操作,地址会跳过 1 个元素的大小(如 4 字节); - “整个数组的地址” 的类型是 “数组指针类型”(如
int(*)[5]),对其进行+1操作,地址会跳过整个数组的大小(如 20 字节)。这一例外的意义在于精准区分 “指向元素” 和 “指向整个数组” 的指针,满足不同场景下的内存操作需求(如数组整体拷贝、多维数组访问等)。
数组作为函数参数
在实际编程中,并非所有对数组的操作都在主函数内完成,常会将数组作为参数传递给其他函数(如专门处理数组的排序、查找函数),而数组作为函数参数时的使用规则,与它在主函数中的使用存在明显区别。
代码演示:
void Print_Arr(int* parr, int size)
{for (int i = 0; i < size; i++){printf("%d ", parr[i]);}printf("\n");
}int main()
{int arr[] = { 1,2,3,4,5,6,7,8,9,10 };int sz = sizeof(arr) / sizeof(arr[0]);Print_Arr(arr, sz);return 0;
}
这段代码实现了一个简易的数组打印功能,核心逻辑围绕数组作为函数参数的特性展开:
- 当数组名
arr作为参数传递给函数时,本质上传递的是数组首元素的地址,而非整个数组。因此,函数的形参必须用指针(如int* parr)来接收这个地址。 - 同时,由于函数内部无法通过
sizeof(parr)计算原数组的大小(此时parr是指针,sizeof(parr)只能得到指针本身的大小),所以必须额外将数组大小sz作为参数传入,才能确保循环遍历的范围正确,避免越界访问。
实现整型数组的冒泡排序(升序)
代码演示:
void Bubble_Sort(int* parr, int size)
{for (int i = 0; i < size; i++){int flag = 1;for (int j = 0; j < size - i - 1; j++){if (parr[j] > parr[j + 1]){int tmp = parr[j];parr[j] = parr[j + 1];parr[j + 1] = tmp;flag = 0;}}if (flag)return;}
}int main()
{int arr[10] = { 0 };int sz = sizeof(arr) / sizeof(arr[0]);// 输入for (int i = 0; i < sz; i++){scanf("%d", &arr[i]);}// 冒泡排序Bubble_Sort(arr, sz);// 输出for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}return 0;
}代码解析:
1. 整体流程
main 函数中先定义了一个包含 10 个元素的数组 arr,通过 sizeof 计算出元素个数 sz。随后通过循环接收用户输入的 10 个数值存入数组,调用 Bubble_Sort 函数进行排序,最后打印排序后的结果。
2. 核心:Bubble_Sort 函数的排序逻辑
该函数接收两个参数:int* parr(指向数组首元素的指针,用于操作数组)和 int size(数组元素个数,控制排序范围)。
-
外层循环:
for (int i = 0; i < size; i++)控制排序的 “轮次”。每一轮循环会将当前未排序部分的最大元素 “冒泡” 到末尾,因此需要size轮(理论上)即可完成全部排序。 -
内层循环:
for (int j = 0; j < size - i - 1; j++)负责每一轮中的元素比较与交换。size - i - 1是关键优化:随着每轮结束,数组末尾会多一个已排好序的最大元素,因此下一轮无需再比较这部分元素,减少了不必要的操作。 -
元素交换与标记:若
parr[j] > parr[j + 1](即前一个元素大于后一个元素),则通过临时变量tmp交换二者位置,确保较小的元素 “上浮”。变量flag初始化为 1(表示 “本轮未交换”),若发生交换则将其置为 0。当某一轮循环结束后flag仍为 1,说明数组已完全有序,可直接通过return提前退出函数,避免后续无效循环 —— 这是冒泡排序的重要优化,能显著提升已有部分有序数组的排序效率。
3. 关键特性
- 由于数组传参本质是传递首元素地址,
Bubble_Sort函数对parr的修改会直接作用于原数组arr,因此排序后main函数中打印的就是已排序的结果。 - 优化后的冒泡排序通过
flag避免了完全有序数组的多余循环,比基础版本更高效,但整体仍适用于数据量较小的场景(时间复杂度为 O (n²))。
