因果推断：因果回归树处理异质性处理效应（三）

本篇文章Understanding Causal Trees适合希望深入了解因果推断的读者。文章的技术亮点在于使用回归树来估计异质性处理效应，提供了一种有效的方式来识别哪些用户对折扣反应更敏感。此外，通过引入辅助结果变量，作者将因果推断问题转化为预测问题，增强了模型的可解释性和准确性。

---

---

1 引言

在因果推断中，我们通常关注估计处理（药物、广告、产品等）对感兴趣结果（疾病、公司收入、客户满意度等）的因果效应。然而，仅仅知道处理平均有效通常是不够的，我们希望了解对于哪些主体（患者、用户、客户等）它效果更好或更差，即我们希望估计异质性处理效应。

估计异质性处理效应使我们能够通过目标定位选择性地、更有效地使用处理。了解哪些客户更有可能对折扣做出反应，可以帮助公司通过提供更少但更精准的折扣来节省开支。
这也适用于负面效应：了解哪些患者对某种药物有副作用，可以帮助制药公司警告他们或将他们排除在治疗之外。估计异质性处理效应还有一个更微妙的优势：了解处理对谁有效，可以帮助我们更好地理解处理如何起作用。如果折扣的效果不取决于接收者的收入，而取决于其购买习惯，这告诉我们可能这不是钱的问题，而是关注度或忠诚度的问题。

在本文中，我们将探讨使用回归树（和森林）的修改版本来估计异质性处理效应。从机器学习的角度来看，因果树和预测树之间存在两个根本区别。首先，目标是处理效应，这是一个本质上不可观测的量。其次，我们关注的是推断，这意味着量化我们估计的不确定性。

1.1 在线折扣与目标定位

在本文的其余部分，我们将使用一个玩具示例进行说明：假设我们是一家在线商店，我们有兴趣了解向新客户提供折扣是否会增加他们的消费。特别是，我们想知道提供折扣是否对某些客户比其他客户更有效，因为我们宁愿不向那些无论如何都会消费的客户提供折扣。此外，向客户发送过多弹窗也可能会阻止他们购买，产生相反的效果。

为了了解折扣是否以及在多大程度上有效，我们进行了一项 A/B 测试：每当新用户访问我们的在线商店时，我们随机决定是否向他们提供折扣。我从 src.dgp 导入数据生成过程 dgp_online_discounts()。相对于之前的文章，我生成了一个新的 DGP 父类来处理随机化和数据生成，而其子类包含特定的用例。我还从 src.utils 导入了一些绘图函数和库。为了不仅包含代码，还包含数据和表格，我使用了 Deepnote，一个类似 Jupyter 的基于网络的协作笔记本环境。

from src.utils import *
from src.dgp import dgp_online_discountsdgp = dgp_online_discounts(n=100_000)
df = dgp.generate_data()
df.head()

我们有 100,000 名网站访问者的数据，我们观察到他们的 time（一天中的时间）、他们使用的 device（设备）、他们的 browser（浏览器）和他们的地理 region（区域）。我们还看到他们是否获得了 discount（折扣），即我们的处理，以及他们的 spend（消费），即感兴趣的结果。

由于处理是随机分配的，我们可以使用简单的均值差异估计量来估计处理效应。我们期望处理组和对照组是相似的，除了 discount，因此我们可以将 spend 的任何差异归因于 discount。

smf.ols('spend ~ discount', df).fit().summary().tables[1]

折扣似乎有效：平均而言，处理组的消费增加了 1.95 美元。但所有客户都受到同等影响吗？

为了回答这个问题，我们希望估计异质性处理效应，可能是在个体层面。

1.2 异质性处理效应

估计异质性处理效应有多种可能的方法。最常见的方法是根据一些可观测特征将人群分成组，在我们的例子中可以是 device、browser 或 region。一旦你决定了根据哪个变量来分割数据，你就可以简单地将处理变量 (discount) 与处理异质性的维度进行交互。例如，我们以 device 为例。

smf.ols('spend ~ discount * device', df).fit().summary().tables[1]

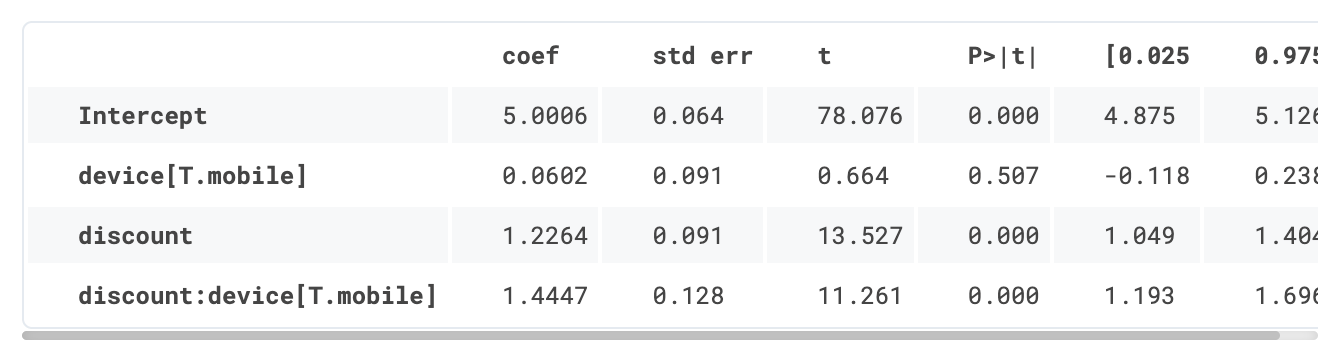
我们如何解释回归结果？discount 对客户 spend 的影响是 1.22 美元，但如果客户通过移动 device 访问网站，则会进一步增加 1.44 美元。

对于分类变量，分割很容易，但对于像 time 这样的连续变量，在哪里分割并不直观。每小时？哪个维度信息量更大？尝试所有可能的分割会很诱人，但我们分割数据越多，就越有可能发现虚假结果（即，用机器学习的行话来说，我们过拟合了）。如果我们可以让数据说话并选择最少和信息量最大的分割，那就太好了。

在[另一篇文章]中，我展示了所谓的元学习器如何采用这种方法进行因果推断。其思想是预测每个观测值在处理状态下的结果，然后比较处理状态下的预测结果与对照状态下的预测结果。差异就是个体处理效应。

元学习器的问题在于它们将所有自由度用于预测结果。然而，我们感兴趣的是预测处理效应的异质性。如果结果的大部分变异不在处理维度上，我们将得到非常差的处理效应估计。

是否可能转而直接专注于个体处理效应的预测？让我们将 Y 定义为感兴趣的结果 spend，D 为处理 discount，X 为其他可观测特征。理想的损失函数是

$$\mathcal{L}({\tau }_i)=\mathbb{E}[(Y_i-{\tau }_i{)}^2|X_i]$$

其中 ${\tau }_i$ 是个体 $i$ 的处理效应。然而，这个目标函数是不可行的，因为我们无法观测到 ${\tau }_i$。

但是，事实证明有一种方法可以获得个体处理效应的无偏估计。其思想是使用一个辅助结果变量，其对每个个体的期望值就是个体处理效应。这个变量是

$$Y_i^{\ast }=\frac{D_i-p(X_i)}{p(X_i)(1-p(X_i))}(Y_i-\mathbb{E}[Y_i|X_i,D_i=0])$$

其中 $p(X_i)$ 是观测值 $i$ 的倾向得分，即其被处理的概率。

在随机实验中，倾向得分是已知的，因为随机化完全在实验者的控制之下。例如，在我们的案例中，处理概率是 50%。而在准实验研究中，当处理概率未知时，需要对其进行估计。即使在随机实验中，估计倾向得分也总是优于插补，因为它能防止随机化中的抽样变异。

我们首先为我们的分类变量 device、browser 和 region 生成哑变量。

df_dummies = pd.get_dummies(df[dgp.X[1:]], drop_first=True)
df = pd.concat([df, df_dummies], axis=1)
X = ['time'] + list(df_dummies.columns)

我们拟合一个 LogisticRegression 并用它来预测处理概率，即构建倾向得分。

from sklearn.linear_model import LogisticRegressiondf['pscore'] = LogisticRegression().fit(df[X], df[dgp.D]).predict_proba(df[X])[:,1]
sns.histplot(data=df, x='pscore', hue='discount').set(title='Predicted propensity scores');

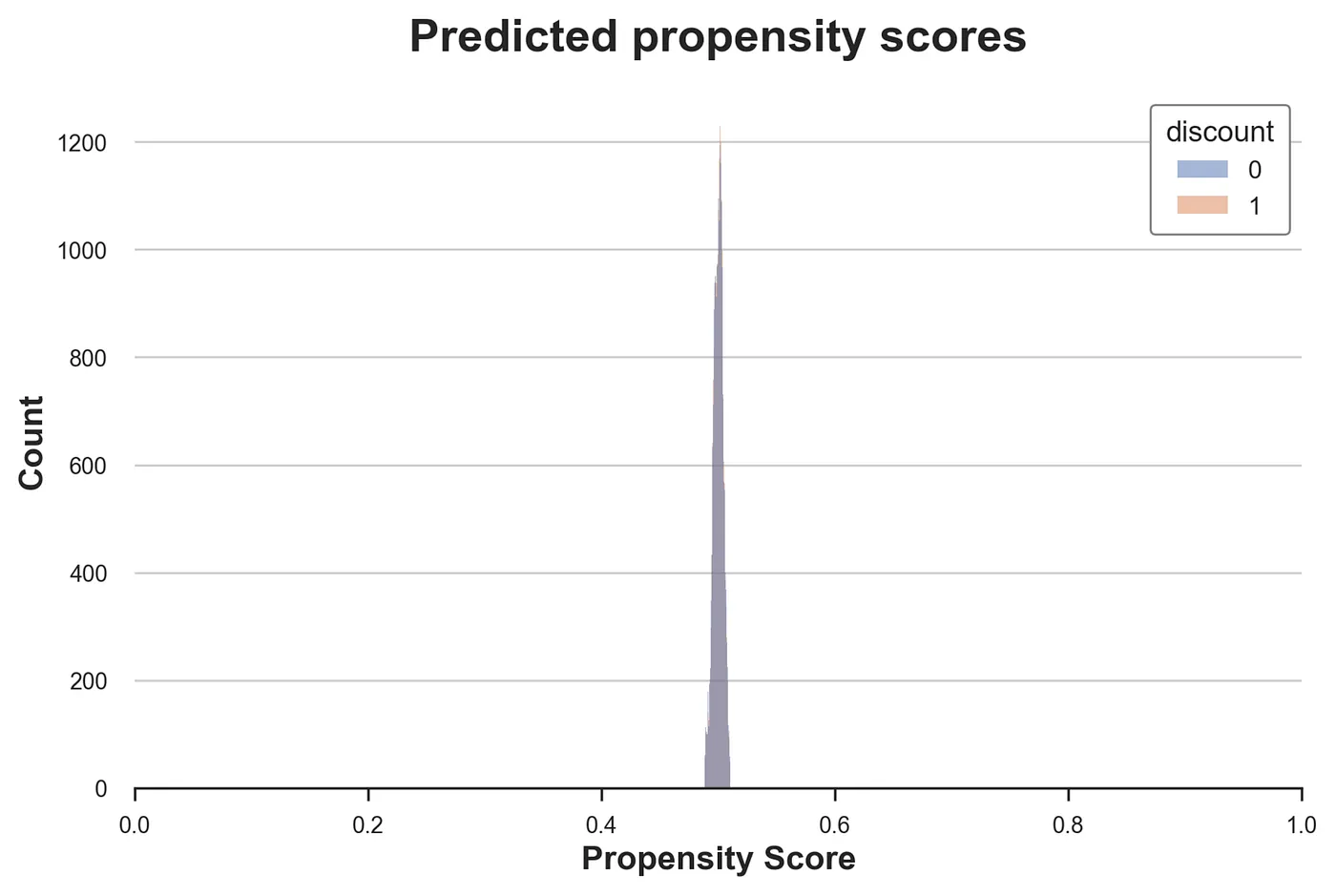
不出所料，大多数倾向得分都非常接近 0.5，这是随机化中使用的处理概率。此外，处理组和对照组的分布几乎相同，进一步证实了随机化是有效的。如果不是这样，我们将需要做出进一步的假设才能进行因果分析。最常见的一个是无混淆性，也称为可忽略性或基于可观测变量的选择。简而言之，我们将假设在某些可观测变量 $\mathcal{X}$ 的条件下，处理分配与随机分配一样好。

$$(Y_i(1),Y_i(0))\perp D_i|{\mathcal{X}}_i$$

然而，在我们的案例中，处理概率是已知的，并且随机化过程似乎没有出现任何问题。

我们现在拥有计算辅助结果变量 $Y^{\ast }$ 的所有要素。

df['y_star'] = df[dgp.Y[0]] / (df[dgp.D] * df['pscore'] - (1-df[dgp.D]) * (1-df['pscore']))

正如我们之前所说，其思想是使用 $Y^{\ast }$ 作为预测问题的目标，因为其期望值恰好是个体处理效应。让我们检查它在数据中的平均值。

df['y_star'].mean()

事实上，它的平均值几乎与之前估计的平均处理效应 1.94 美元完全相同。

为什么我们能够通过单个观测值和倾向得分的估计来估计个体处理效应？有什么缺点？

直觉是从不同的角度来解决这个问题：事前，在实验之前。想象一下我们的数据集只有一个观测值，i。我们知道处理概率是 $p(X_i)$，即倾向得分。因此，在期望上，我们的数据集有 $p(X_i)$ 个观测值在处理组中，$1-p(X_i)$ 个观测值在对照组中。其余的照常进行：我们将处理效应估计为两组平均结果的差异！这正是我们要做的事情：

$$Y_i^{\ast }=\frac{D_i{Y}_i}{p(X_i)}-\frac{(1-D_i)Y_i}{1-p(X_i)}$$

唯一的区别是我们只有一个观测值。

这个技巧是有代价的：$Y_i^{\ast }$ 是个体处理效应的无偏估计量，但其方差非常大。通过绘制其分布可以立即看出这一点。

sns.histplot(df['y_star']).set(title='Distribution of Auxiliary Variable');

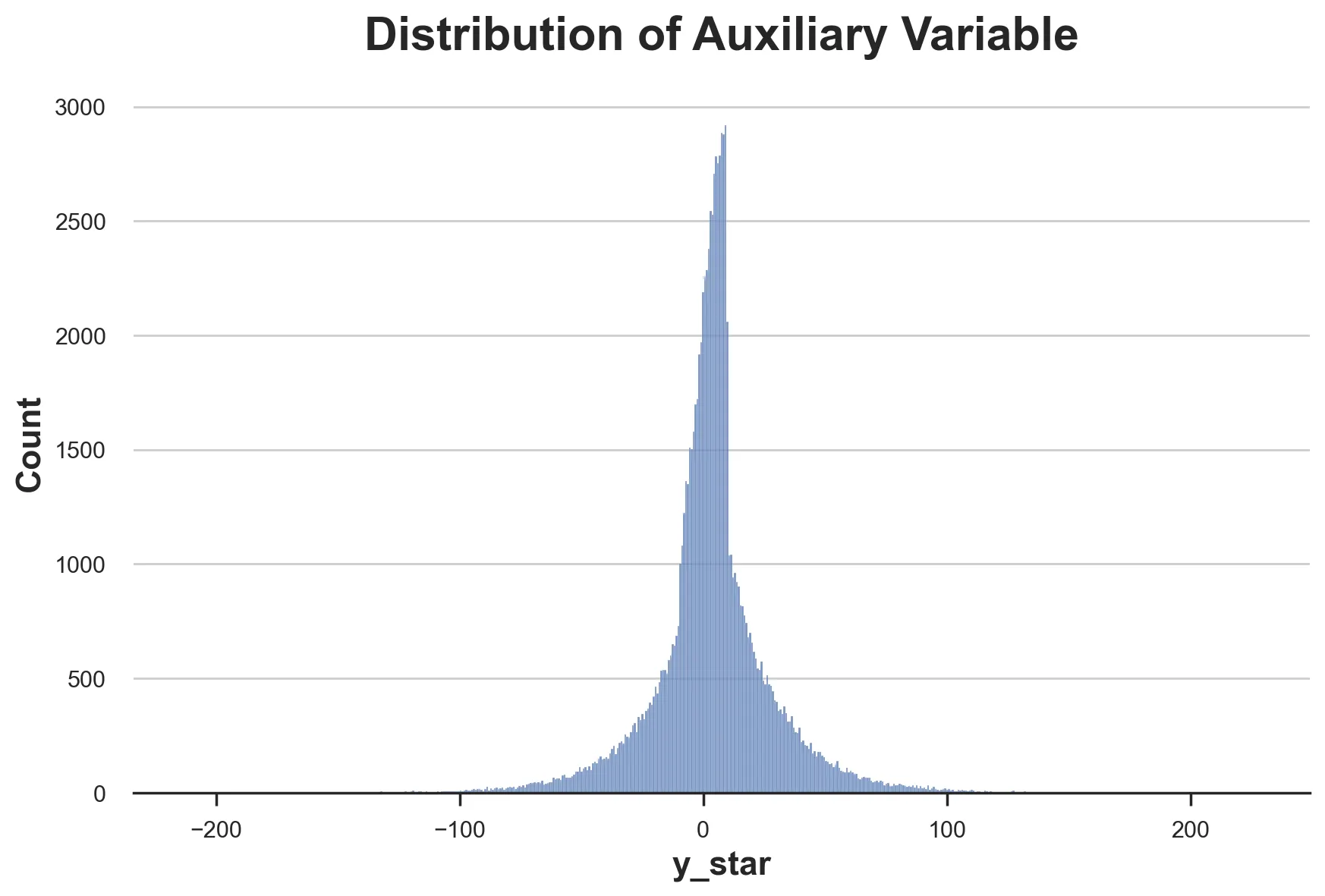
我们现在准备估计异质性处理效应，通过将因果推断问题转化为一个预测问题，预测辅助结果 $Y^{\ast }$，给定可观测特征 $X$。

2 因果回归树

在上一节中，我们已经看到可以将异质性处理效应的估计转化为一个预测问题，其中结果是辅助结果变量

$$Y_i^{\ast }=\frac{D_i-p(X_i)}{p(X_i)(1-p(X_i))}(Y_i-\mathbb{E}[Y_i|X_i,D_i=0])$$

原则上，我们此时可以使用任何机器学习算法来估计个体处理效应。然而，回归树具有特别方便的特性。

首先，回归树是如何工作的？
分类和回归树 (CART) 算法根据协变量 $X$ 递归地将数据分割成箱，使得每个箱内的结果 $Y$ 尽可能同质，而箱之间的结果尽可能异质。
预测值简单地是每个箱内的结果平均值，在我们的例子中是辅助结果变量 $Y^{\ast }$，其对每个观测值的期望值等于个体处理效应。
因此，通过对每个箱内的 $Y^{\ast }$ 求平均，我们可以计算落入该箱的观测值的条件（基于 X）异质性处理效应 $\mathbb{E}[{\tau }_i|X_i]$。

平均部分是回归树用于推断的一大优势，因为我们非常清楚如何利用中心极限定理对平均值进行推断。
回归树相对于其他机器学习算法的第二个优势是树非常可解释，因为我们可以直接将数据分区绘制成树状结构。我们稍后会看到更多。最后但同样重要的是，截至 2022 年，回归树仍然是表格数据性能最佳预测算法的核心。

让我们使用 sklearn 中的 DecisionTreeRegressor 函数来拟合我们的回归树，并估计 discounts 对客户 spend 的异质性处理效应。

from sklearn.tree import DecisionTreeRegressortree = DecisionTreeRegressor(max_depth=2).fit(df[X], df['y_star'])
df['y_hat'] = tree.predict(df[X])

我们已将树限制为最大深度为 2，并且每个分区（也称为_叶子_）至少有 30 个观测值，以便我们可以轻松绘制树并可视化估计的组和处理效应。

from sklearn.tree import plot_treeplot_tree(tree, filled=True, fontsize=12, feature_names=X, impurity=False, rounded=True);

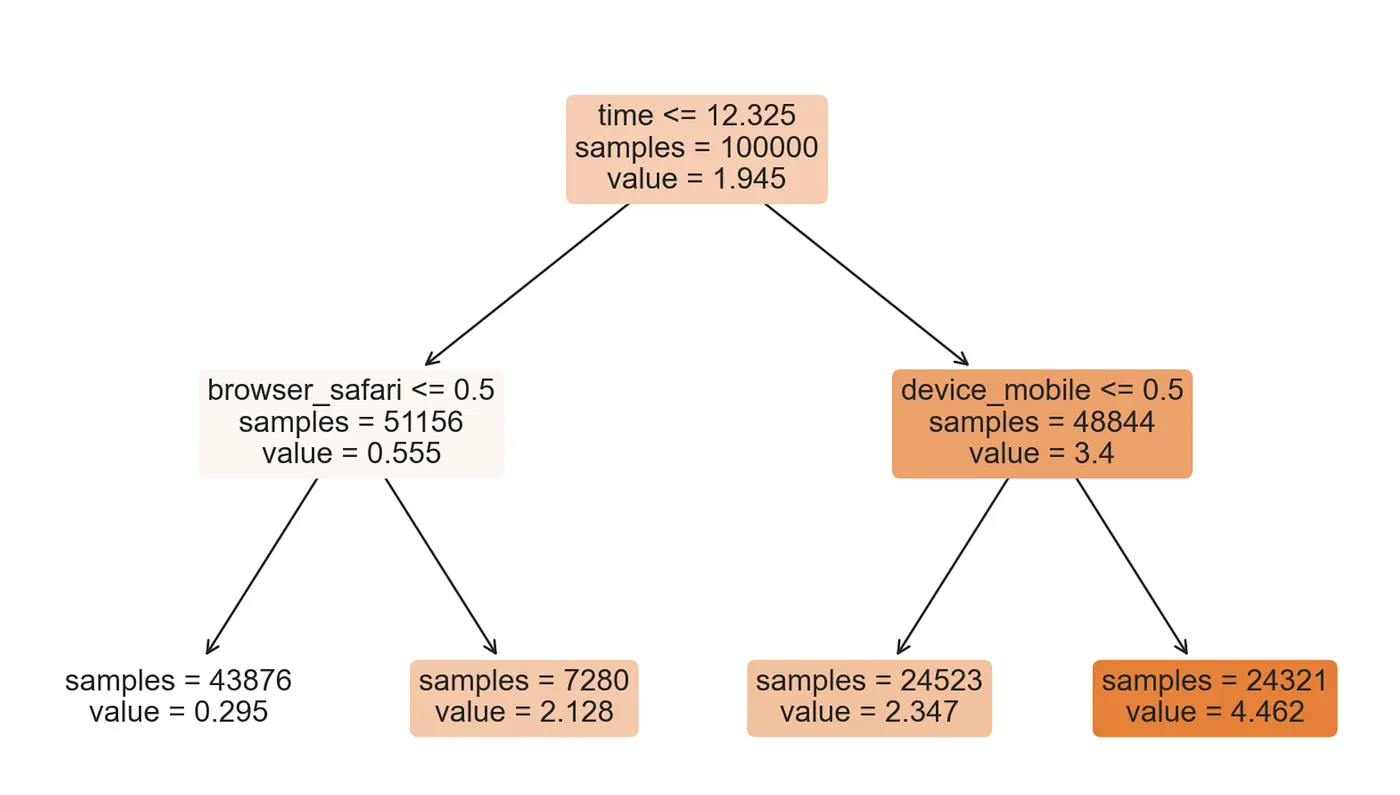
我们应该如何解释这棵树？在顶部，我们可以看到数据中 $Y^{\ast }$ 的平均值，1.945 美元，对应于平均处理效应。从那里开始，数据根据每个节点顶部突出显示的规则分成不同的分支。例如，第一个节点根据 time 是否晚于 12.325 将数据分成两个组，大小分别为 51,156 和 48,844。在底部，我们有最终的分区，以及异质性处理效应。例如，最左边的叶子包含 43,876 个观测值，其 time 早于 12.325 且浏览器不是 Safari，我们预测其对 spend 的影响为 0.295 美元。简而言之，每个节点都包含条件平均处理效应 $\mathbb{E}[{\tau }_i|X_i]$ 的估计，其中节点颜色越深表示预测值越高。

我们应该相信这些估计吗？不完全是，原因有几个。
第一个问题是，只有当每个叶子内部处理单元和对照单元的数量相同时，我们才能得到平均处理效应的无偏估计。
这并非 DecisionTreeRegressor() 开箱即用的情况。

2.1 Honest Trees

我们朴素过程的另一个问题是，我们使用了相同的数据来生成树并评估它。这会产生偏差，因为简单的均值差异估计量不会考虑分区是内生的，即在相同数据上生成的。用机器学习的术语来说，我们正在过拟合。解决方案很简单：我们可以将样本分成两个独立的子样本，并使用不同的数据来生成树和计算预测。这些树被称为Honest Trees。

这个解决方案既简单又有效，因为它允许我们在推断阶段将叶子中的每个样本视为独立于树结构。此时，我们的估计量是一个均值差异估计量，对于一个独立的子样本，我们可以简单地使用中心极限定理进行推断。分割数据的一个缺点是我们会失去功效，即检测非虚假异质性处理效应的能力，因为样本量较小。解决方案是重复该过程两次，交换用于构建树的样本和用于计算叶内平均值的样本。然后，我们可以对每个个体的两个估计值进行平均，并相应地调整估计的标准误差。

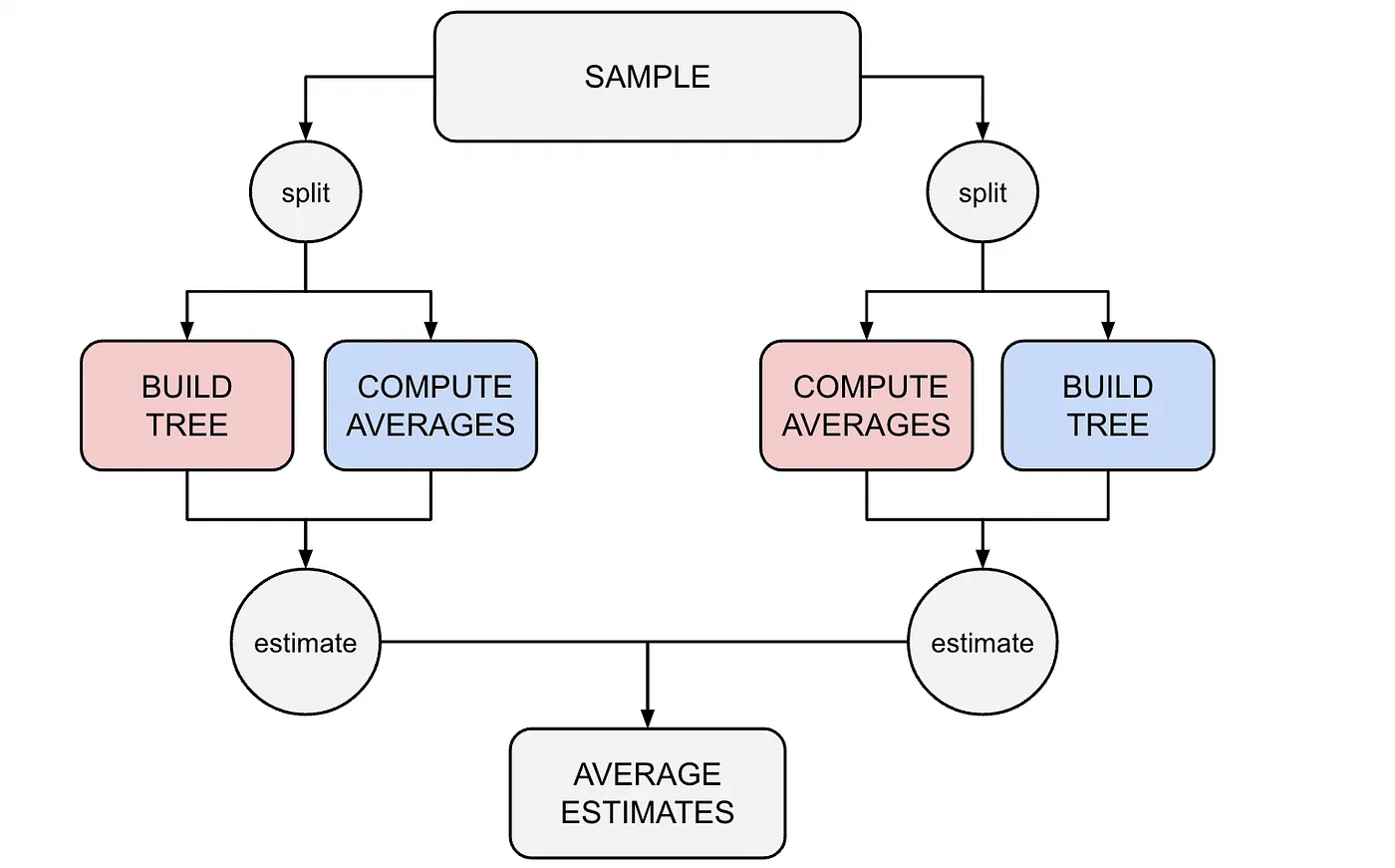
2.2 生成分裂

最后但同样重要的是，树应该如何生成？DecisionTreeRegressor 函数生成分裂的默认规则是 squared_error，并且对每个叶子的最小观测数没有限制。其他常用的规则包括平均绝对误差、基尼不纯度（Gini’s impurity）和香农信息（Shannon’s information）。哪种表现更好取决于具体的应用，但总体目标始终是预测准确性，广义而言。

在我们的案例中，目标是推断：我们希望发现统计上彼此不同的异质性处理效应。如果不同的处理效应在统计上无法区分，那么生成它们就没有价值。此外（但密切相关），在构建树和生成数据分区时，我们必须考虑到，由于我们使用诚实树，我们将使用不同的数据来估计叶内处理效应。

Athey 和 Imbens (2016) 使用了修改版的均方误差 (MSE) 作为分裂标准，即扩展均方误差 (EMSE)：

$$\text{EMSE}=\mathbb{E}[Y_i^{\ast 2}-2Y_i^{\ast }\mu (X_i)+\mu (X_i{)}^2]$$

其中 $\mu$ 是估计的条件期望 $\mu (X)=\mathbb{E}[Y^{\ast }|X]$，与 MSE 的区别在于额外的项 $Y_i^2$，即平方结果变量。在我们的设置中，我们可以将其改写为

$$\text{EMSE}=\mathbb{E}[Y_i^{\ast 2}|X_i]-(\mathbb{E}[Y_i^{\ast }|X_i]{)}^2$$

为什么这是一个合理的损失函数？因为我们可以将其改写为条件处理效应估计量 $\tau (X)$ 的期望方差减去其平方期望值。

$$\text{EMSE}=\text{Var}(\tau (X))-(\mathbb{E}[\tau (X)]{)}^2$$

EMSE 的这种表述清楚地表明，目标是最小化估计的条件处理效应 $\tau (X)$ 的叶内方差（第一项）。换句话说，小的叶子会自动受到惩罚。第二项只是一个归一化因子。请注意，这两项都是未知的，必须从用于生成树的训练数据中估计。

2.3 实现方式：EconML

幸运的是，有多个因果树库。我们从微软的 EconML 库中导入 CausalForestDML，它是因果推断的最佳库之一。

from econml.dml import CausalForestDML
tree_model = CausalForestDML(n_estimators=1, subforest_size=1, inference=False, max_depth=4)
tree_model = tree_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])

我们已将估计器数量限制为 1，以获得单棵树而不是多棵树，即我们将在单独文章中介绍的所谓随机森林。

from econml.cate_interpreter import SingleTreeCateInterpreterintrp = SingleTreeCateInterpreter(max_depth=2).interpret(tree_model, df[X])
intrp.plot(feature_names=X, fontsize=12)

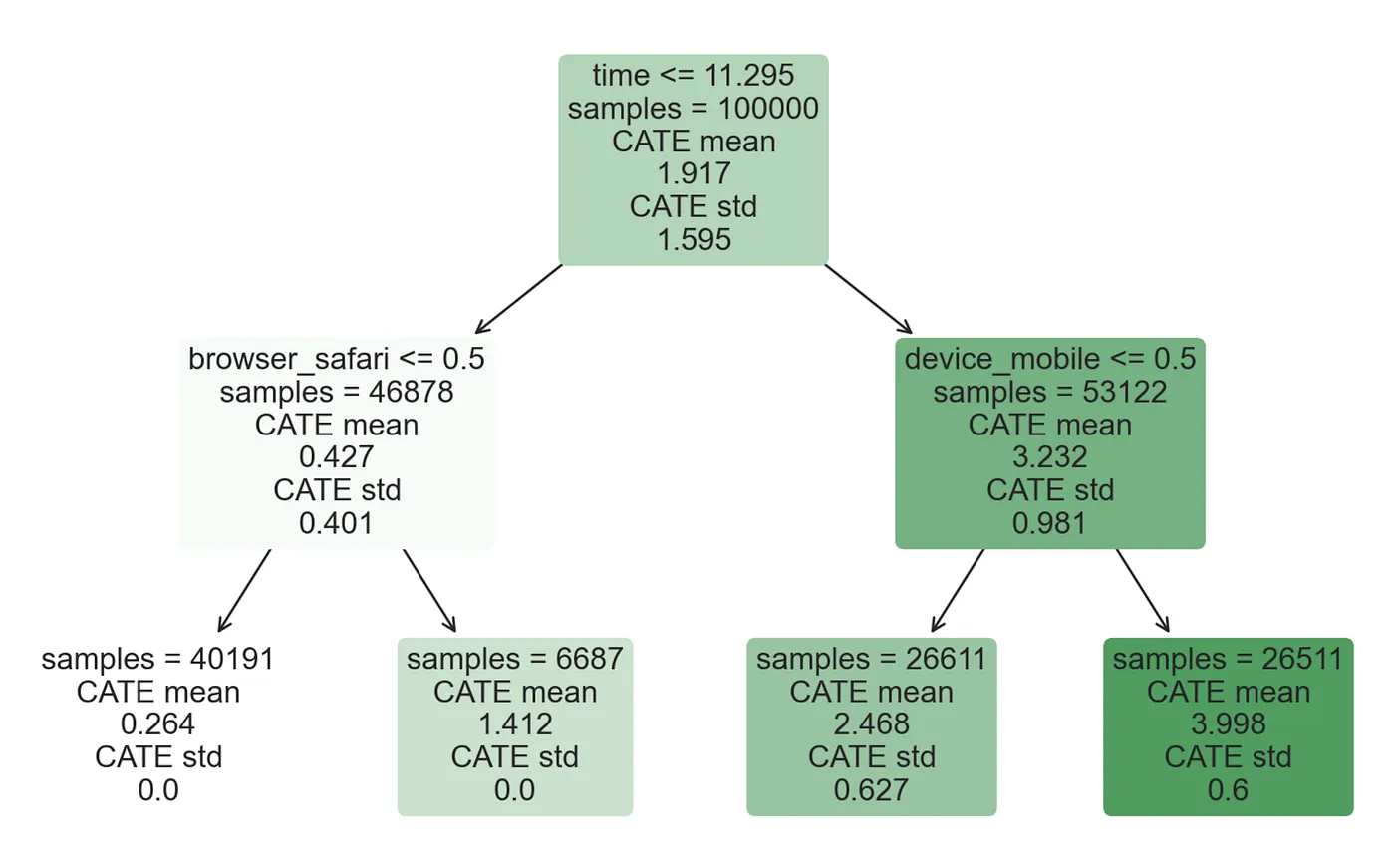
正如我们所看到的，树的表示与我们之前使用 DecisionTreeRegressor 函数得到的非常相似。然而，现在模型不仅报告了条件平均处理效应的估计，还报告了估计的标准误差（在底部）。它们是如何计算的？

2.4 推断

诚实树除了提高模型的样本外预测准确性外，还有一个重要的意义：它们允许我们计算标准误差，就像树结构是外生的一样。事实上，由于用于计算预测的数据独立于用于构建树（分割数据）的数据，我们可以将树结构视为与估计的处理效应无关。因此，我们可以将估计的标准误差估计为样本平均值之间差异的标准误差，就像在标准 AB 测试中一样。

如果我们使用相同的数据来构建树和估计处理效应，我们就会引入偏差，因为协变量和结果之间存在虚假相关性。这种偏差通常在样本量非常大时消失，但诚实树不需要这样做。

2.5 计算性能

模型表现如何？由于我们控制数据生成过程，我们可以做一些真实数据无法做到的事情：将预测的处理效应与真实的处理效应进行比较。add_treatment_effect() 函数为数据中的每个观测值提供了“真实”的处理效应。

def compute_discrete_effects(df, hte_model):temp_df = df.copy()temp_df.time = 0temp_df = dgp.add_treatment_effect(temp_df)temp_df = temp_df.rename(columns={'effect_on_spend': 'True'})temp_df['Predicted'] = hte_model.effect(temp_df[X])df_effects = pd.DataFrame()for var in X[1:]:for effect in ['True', 'Predicted']:v = temp_df[effect][temp_df[var]==1].mean() - temp_df[effect][temp_df[var]==0].mean()effect_var = {'Variable': [var], 'Effect': [effect], 'Value': [v]}df_effects = pd.concat([df_effects, pd.DataFrame(effect_var)]).reset_index(drop=True)return df_effects, temp_df['Predicted'].mean()df_effects_tree, avg_effect_notime_tree = compute_discrete_effects(df, tree_model)

我们现在可以检查因果树估计个体处理效应的能力。让我们从分类变量开始。我绘制了在 device、browser 和 region 的每个值条件下真实和估计的平均处理效应。

ig, ax = plt.subplots()
sns.barplot(data=df_effects_tree, x="Variable", y="Value", hue="Effect", ax=ax).set(xlabel='', ylabel='', title='Heterogeneous Treatment Effects')
ax.set_xticklabels(ax.get_xticklabels(), rotation=45, ha="right");

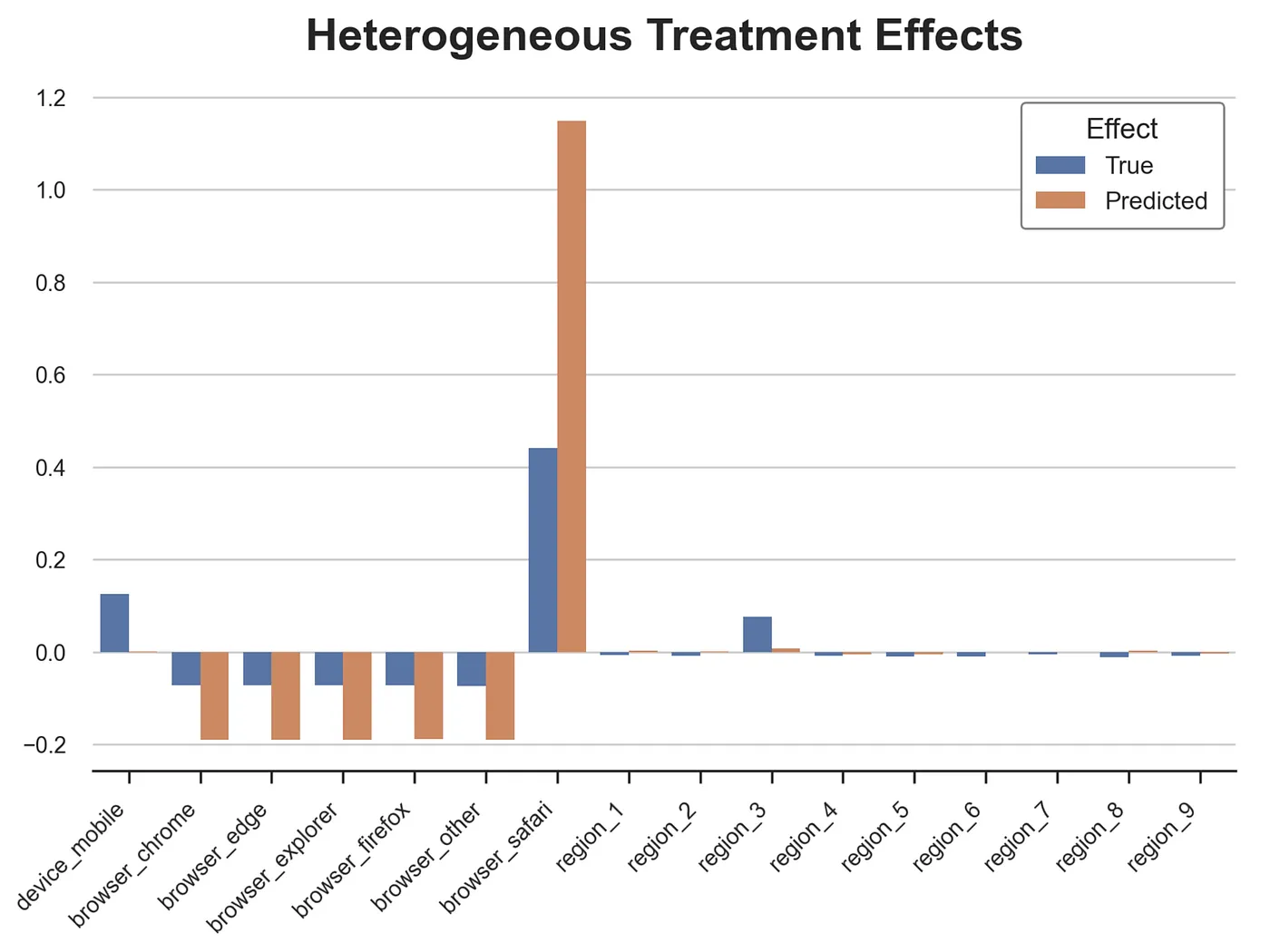
因果树在检测分类变量的异质性处理效应方面表现出色。它高估了移动设备和 Safari 浏览器的影响，但总体上做得很好。

然而，这也是我们期望树模型表现特别好的地方：效应是离散的。那么它在我们的连续变量 time 上表现如何呢？首先，让我们再次分离出对 time 的预测处理效应，并忽略其他协变量。

def compute_time_effect(df, hte_model, avg_effect_notime):df_time = df.copy()df_time[[X[1:]] + ['device', 'browser', 'region']] = 0df_time = dgp.add_treatment_effect(df_time)df_time['predicted'] = hte_model.effect(df_time[X]) + avg_effect_notimereturn df_timedf_time_tree = compute_time_effect(df, tree_model, avg_effect_notime_tree)

我们现在绘制沿 time 维度预测的处理效应与真实的处理效应。

sns.scatterplot(x='time', y='effect_on_spend', data=df_time_tree, label='True')
sns.scatterplot(x='time', y='predicted', data=df_time_tree, label='Predicted').set(ylabel='', title='Heterogeneous Treatment Effects')
plt.legend(title='Effect');

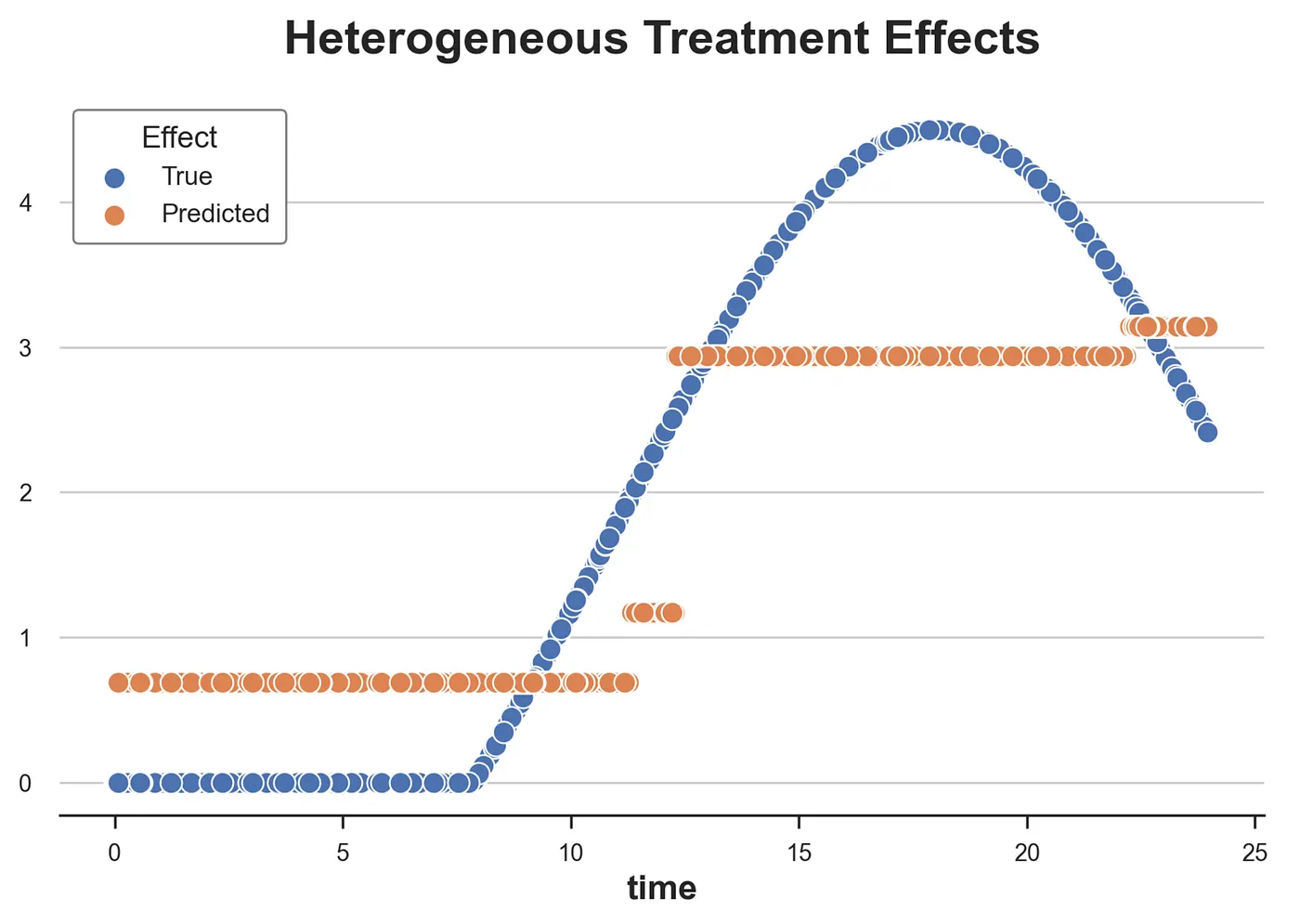
从图中我们可以看出因果树的离散性质：模型只能将连续变量分割成 4 个箱。这些箱接近真实的处理效应，但未能捕捉到处理效应异质性的一大部分。

这些预测可以改进吗？答案是肯定的，我们将在下一篇文章中探讨如何改进。

3 结论

在本文中，我们探讨了如何使用因果树来估计异质性处理效应。主要见解来自于辅助结果变量的定义，它使我们能够将推断问题构建为预测问题。虽然我们随后可以使用任何算法来预测处理效应，但回归树因其可解释性、预测准确性以及将预测生成为子样本平均值的特性而特别有用。

Athey 和 Imbens (2016) 关于回归树计算异质性处理效应的工作，将因果推断和机器学习这两个独立的文献领域以富有成效的协同方式结合起来。
因果推断文献（重新）发现了样本分割的推断优势，这使我们即使在数据分区复杂且难以分析的情况下也能进行正确的推断。另一方面，将树生成阶段与叶内预测阶段分离，在预测准确性方面具有显著优势，通过防止过拟合来保障。

3.1 参考文献

• S. Athey, G. Imbens, Recursive partitioning for heterogeneous causal effects (2016), PNAS。
• S. Wager, S. Athey, Estimation and Inference of Heterogeneous Treatment Effects using Random Forests (2018), Journal of the American Statistical Association。
• S. Athey, J. Tibshirani, S. Wager, Generalized Random Forests (2019)。 The Annals of Statistics。
• M. Oprescu, V. Syrgkanis, Z. Wu, Orthogonal Random Forest for Causal Inference (2019)。 Proceedings of the 36th International Conference on Machine Learning。

3.2 代码

您可以在这里找到原始的 Jupyter Notebook：

https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/causal\_trees.ipynb