当前位置：首页 > news >正文

力扣1895. 最大的幻方

news 2025/9/20 11:23:42

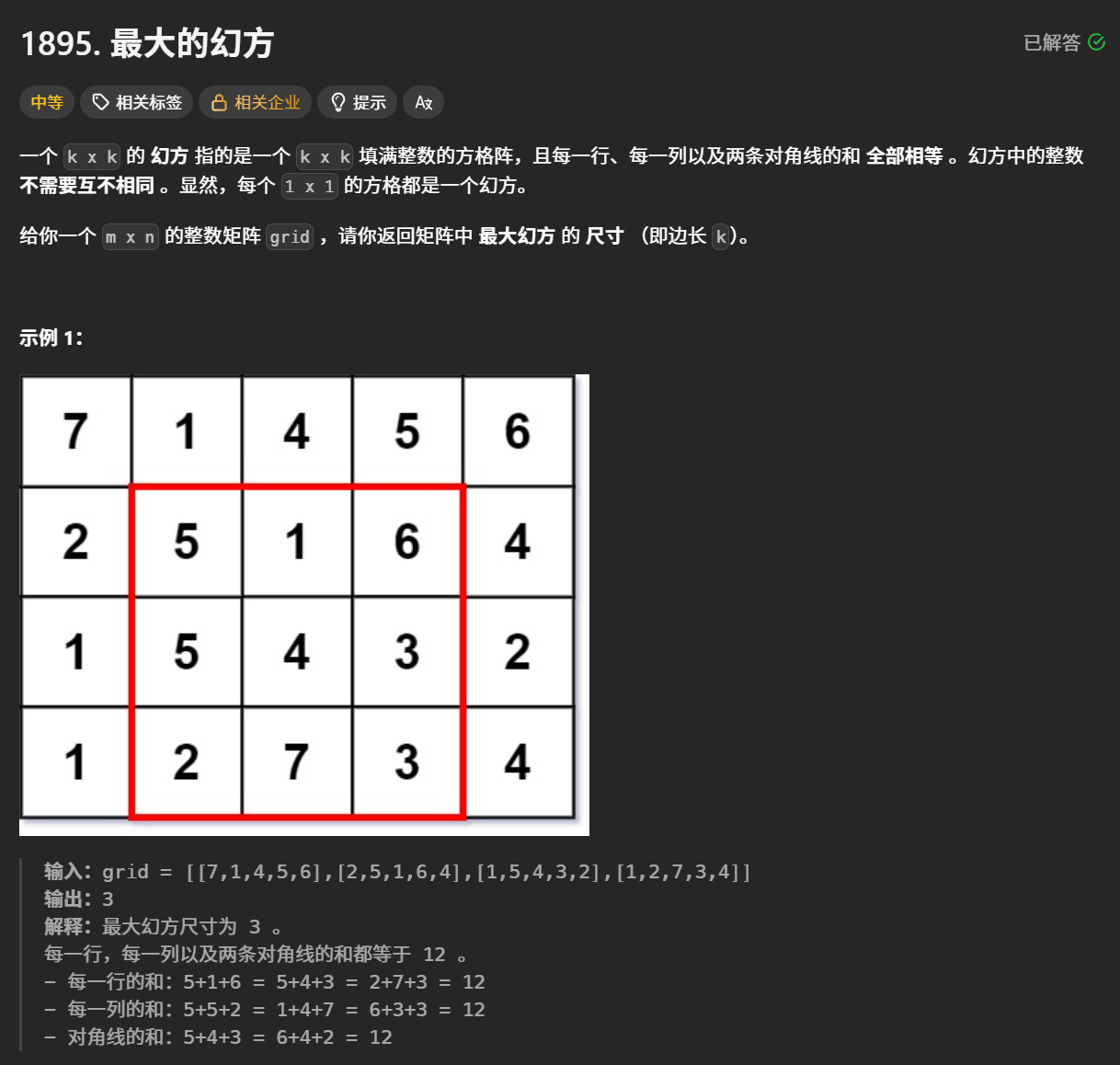
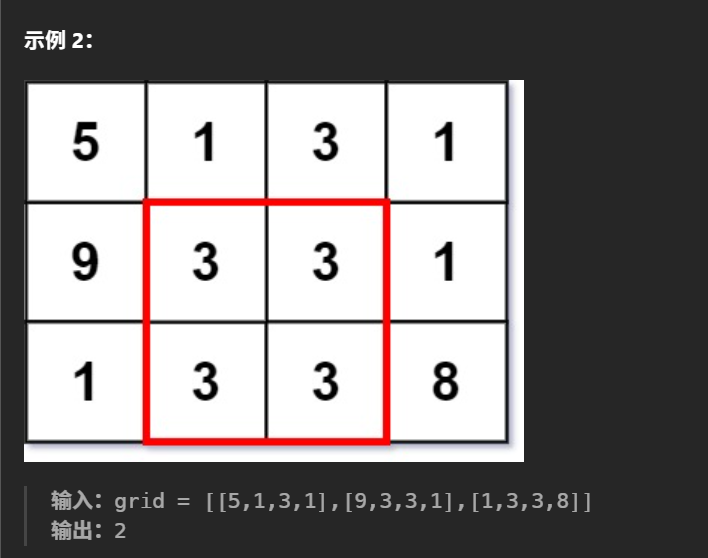
在这里插入图片描述

这一题的大意是让我们在一个大的矩阵中找到一个边长最大的正方形，使得该正方形的每一行每一列和两条对角线完全相等。
我们只需要从大到小的枚举边长，在枚举过边长的基础上枚举所有符合该边长的正方形。
在计算每一行每一列的和的时候可以用前缀和来优化
因为如果我们不优化：
枚举边长的大概是O（n），枚举所有符合条件的正方形又是O（n^2)
再计算每一行和列的和的时间复杂度都约等于O（n），
再将每一行，每一列，对角线比较是否相等的时间复杂度也为O（n）。
所以时间复杂度大概为O（n^5)
O(n⁵) = 50⁵ = 312,500,000 ≈ 3.1e8
时间复杂度是比较大的，
因此我们需要对其进行优化，我们会发现，在计算每一行每一列的和的时候，我们可以进行前缀和的优化，即提前算出每一行，每一列的前缀和，这样就不用在枚举矩阵的时候计算每一行或列的和了。
这样时间复杂度也降到了O（n^4),可以通过。
很明显需要知道的是，不管用不用前缀和优化，在遇到矩阵枚举的时候，我们都可以选择前缀和优化，这是一种常用的做法。
因此，这一题的本质就是矩阵枚举问题通常要枚举边长 + 枚举起点。前缀和优化：遇到“重复计算某一行/列/子矩阵和”的情况，第一反应就是前缀和。
完整代码如下：

class Solution {
public:int largestMagicSquare(vector<vector<int>>& grid) {int ans=1;int m=grid.size();int n=grid[0].size();vector<vector<int> > colsum(m,vector<int>(n));vector<vector<int> > rowsum(m,vector<int>(n));for(int i=0;i<m;i++){rowsum[i][0]=grid[i][0];for(int j=1;j<n;j++){rowsum[i][j]=rowsum[i][j-1]+grid[i][j];}}for(int j=0;j<n;j++){colsum[0][j]=grid[0][j];for(int i=1;i<m;i++){colsum[i][j]=colsum[i-1][j]+grid[i][j];}}for(int edge=min(m,n);edge>=2;edge--){for(int i=0;i+edge-1<m;i++){for(int j=0;j+edge-1<n;j++){int stdsum;if(j!=0)stdsum=rowsum[i][j+edge-1]-rowsum[i][j-1];elsestdsum=rowsum[i][j+edge-1]-0;bool flag=0;for(int ii=i+1;ii<=i+edge-1;ii++){int nowsum;if(j!=0)nowsum=rowsum[ii][j+edge-1]-rowsum[ii][j-1];elsenowsum=rowsum[ii][j+edge-1]-0;if(nowsum!=stdsum){flag=1;break;}}if(flag==1){continue;}for(int jj=j;jj<=j+edge-1;jj++){int nowsum;if(i!=0)nowsum=colsum[i+edge-1][jj]-colsum[i-1][jj];elsenowsum=colsum[i+edge-1][jj]-0;if(nowsum!=stdsum){flag=1;break;}}if(flag==1){continue;}int d1=0;int d2=0;for(int k=0;k<edge;k++){d1+=grid[i+k][j+k];d2+=grid[i+k][j+edge-1-k];}if(d1==stdsum&&d2==stdsum){ans=edge;return edge;}}}}return ans;}};