理解元学习器 - 如何使用机器学习估计异质处理效应(四)
本篇文章Understanding Meta Learners. How to use machine learning to estimate heterogeneous treatment effects适合对因果推断和机器学习感兴趣的读者。文章的亮点在于介绍了S-learner、T-learner和X-learner三种方法,灵活地估计不同用户的处理效应,帮助更好地进行个性化决策。
文章目录
- 1 引言
- 1.1 如何使用机器学习估计异质处理效应
- 1.2 示例
- 2 案例解析
- 2.1 背景设定
- 2.2 S-学习器 (S-Learner)
- 2.3 T-学习器 (T-Learner)
- 2.4 X-学习器 (X-Learner)
- 3 结论
- 4 参考文献
- 5 代码
1 引言
1.1 如何使用机器学习估计异质处理效应
在许多情况下,我们不仅对估计因果效应感兴趣,还对这种效应是否因不同用户而异感兴趣。我们可能想了解某种药物的副作用是否因不同年龄的人而异。或者我们可能想了解某个广告活动在某些地理区域是否特别有效。
这些知识至关重要,因为它使我们能够针对性地进行干预。如果某种药物对儿童有严重的副作用,我们可能希望将其分发限制给成年人。或者如果某个广告活动只在英语国家有效,那么在其他地方展示它就没有意义。
在这篇博客文章中,我们将探讨一些揭示处理效应异质性的方法。特别是,我们将探讨利用机器学习算法灵活性的方法。
1.2 示例
假设我们是一家公司,有兴趣了解一项新的高级功能能增加多少收入。我们知道不同年龄的用户有不同的消费习惯,并且我们怀疑高级功能的影响也可能因用户的年龄而异。
这些信息可能非常重要,例如用于广告定位或折扣设计。如果我们发现高级功能能增加特定用户群体的收入,我们可能希望将广告定位到该群体或为他们提供个性化折扣。
为了了解高级功能对收入的影响,我们进行了一项 AB测试,其中我们随机向测试样本中10%的用户提供高级功能的访问权限。该功能昂贵,我们无法免费提供给更多用户。希望10%的处理概率足够。
我们使用 [src.dgp](https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/src/dgp.py) 中的数据生成过程 dgp_premium() 生成模拟数据。我还从 [src.utils](https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/src/utils.py) 导入了一些绘图函数和库。
from src.utils import *
from src.dgp import dgp_premium
dgp = dgp_premium()
df = dgp.generate_data(seed=5)
df.head()
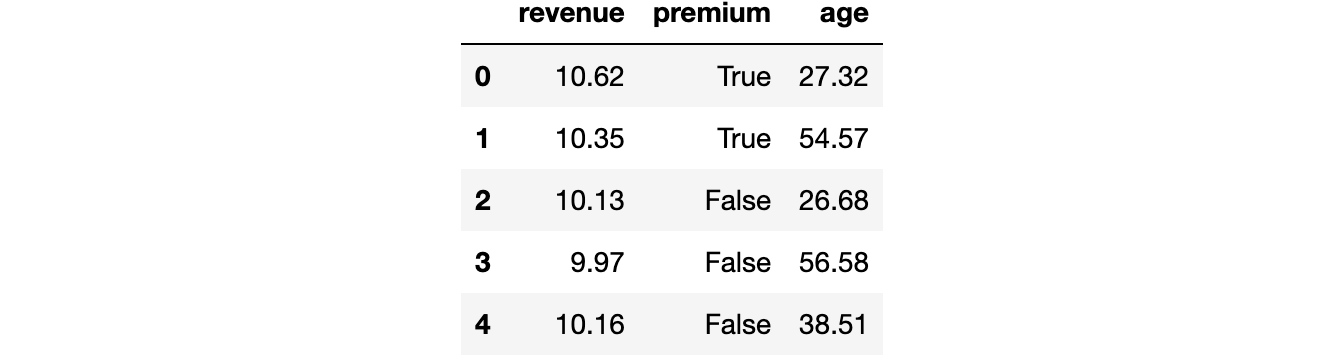
我们有300名用户的数据,我们观察了他们产生的 revenue(收入)以及他们是否获得了 premium(高级)功能。此外,我们还记录了用户的 age(年龄)。
为了了解随机化是否有效,我们使用 Uber 的 [causalml](https://causalml.readthedocs.io/) 包中的 create_table_one 函数生成了一个协变量平衡表,其中包含处理组和对照组之间可观测特征的平均值。顾名思义,这应该是因果推断分析中始终呈现的第一个表格。
from causalml.match import create_table_onecreate_table_one(df, 'premium', ['age', 'revenue'])
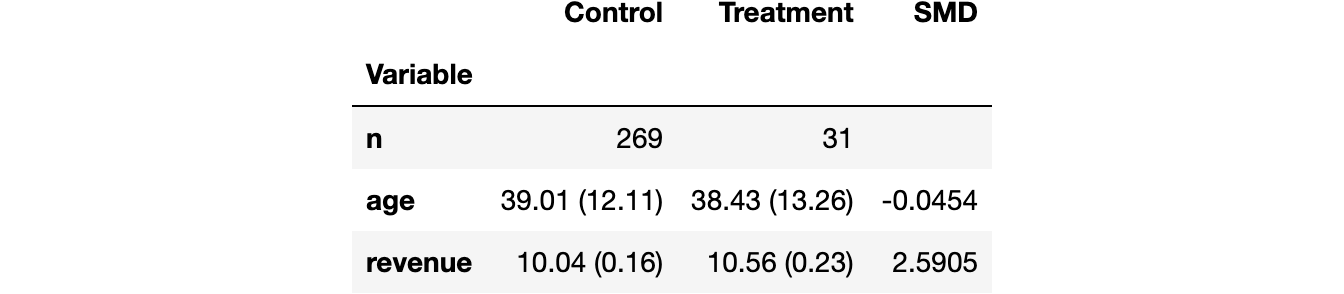
大多数用户属于对照组,只有31名用户获得了高级功能。各组的平均 age 具有可比性(标准化均值差,SMD<0.1),而高级功能似乎平均使每位用户的 revenue 增加了2.59美元。
premium 功能的效果是否因用户 age 而不同?
一个简单的方法是回归 revenue 对 premium 和 age 的完全交互项。
linear_model = smf.ols('revenue ~ premium * age', data=df).fit()
linear_model.summary().tables[1]
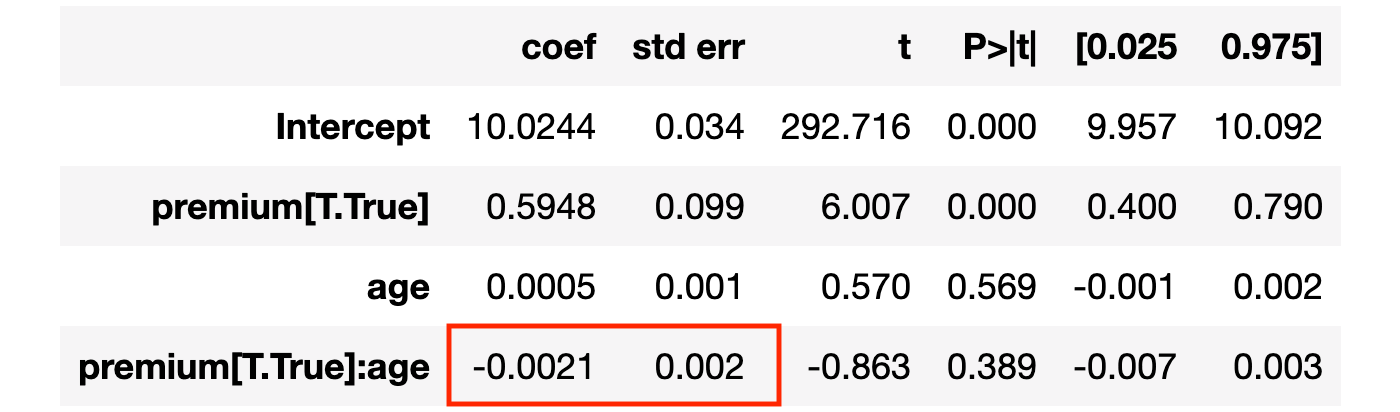
交互项系数接近零且不显著。这似乎表明 premium 对 age 没有差异效应。但这真的正确吗?交互项系数只捕捉线性关系。如果关系是非线性的怎么办?
我们可以通过直接绘制原始数据来检查。我们绘制 revenue 对 age 的散点图,将数据分为 premium 用户和非 premium 用户。
sns.scatterplot(data=df, x='age', y='revenue', hue='premium', s=40);
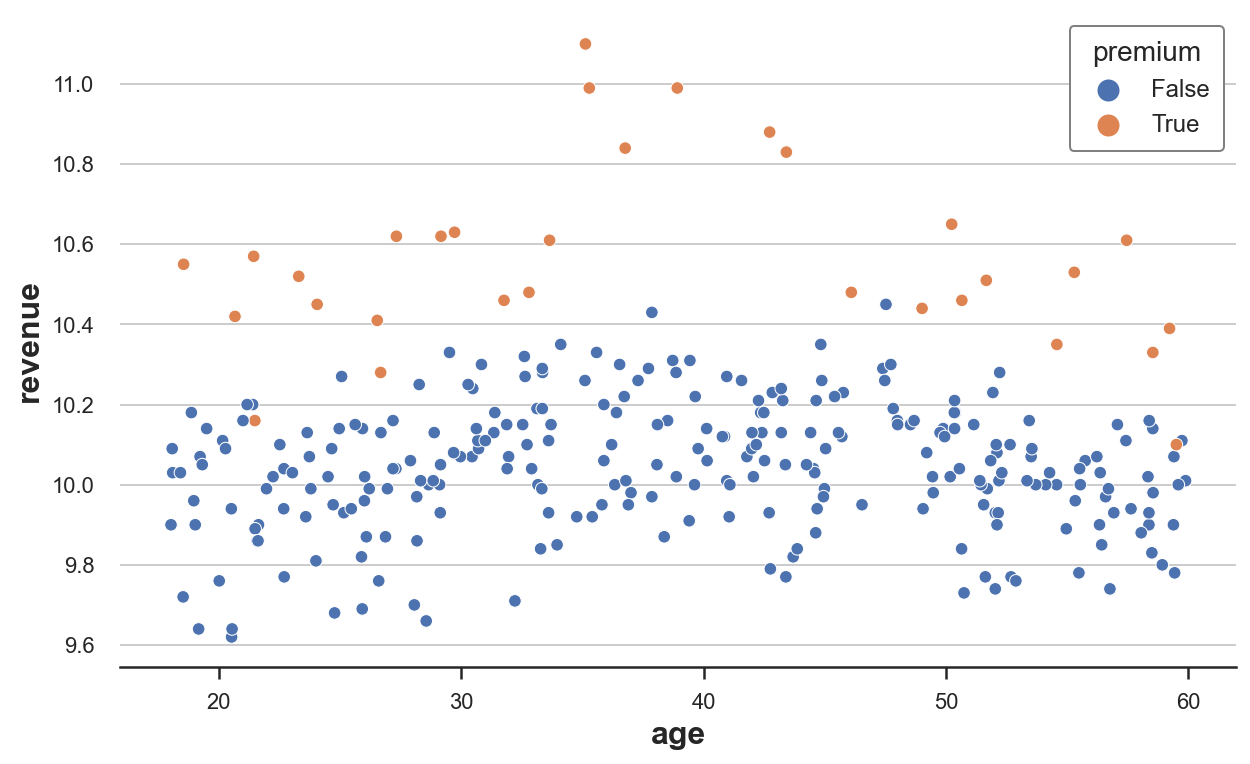
从原始数据来看,revenue 通常在30到50岁之间的人群中较高,而 premium 对35到45岁之间的人群有特别强烈的效果。
我们可以可视化估计的按年龄划分的、有无处理的收入。
我们首先计算有 premium 功能(μ^1\hat{\mu}_1μ^1)和没有 premium 功能(μ^0\hat{\mu}_0μ^0)时的预测收入,并将它们与原始数据一起绘制。
df['mu0_hat'] = linear_model.predict(df.assign(premium=0))
df['mu1_hat'] = linear_model.predict(df.assign(premium=1))
plot_TE(df)
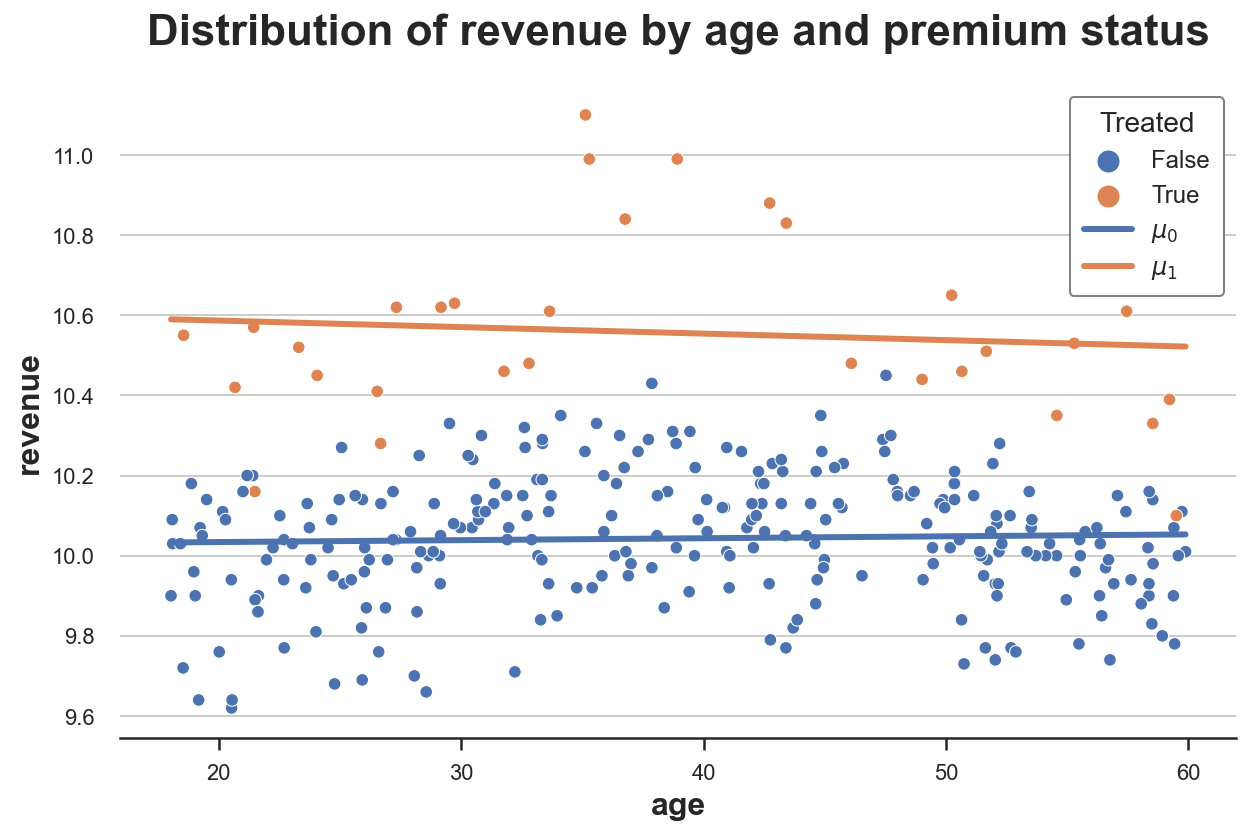
正如我们所看到的,橙色线高于蓝色线,这表明 premium 对 revenue 有积极影响。然而,这两条线基本平行,表明处理效应没有异质性。
我们能更精确吗?有没有办法以灵活的方式估计这种处理异质性,而不假设函数形式?
答案是肯定的!我们可以使用机器学习方法灵活地估计异质处理效应。特别是,我们将检查 Künzel, Sekhon, Bickel, Yu, (2019) 引入的三种流行方法:
- S-学习器 (S-learner)
- T-学习器 (T-learner)
- X-学习器 (X-learner)
2 案例解析
2.1 背景设定
我们假设对于一组个体 i=1,…,ni=1, \dots, ni=1,…,n,我们观察到一个元组 $ (X_i, D_i, Y_i) $,其中包括:
- 处理分配 Di∈{0,1}D_i \in \{0,1\}Di∈{0,1} (
premium) - 响应 Yi∈RY_i \in \mathbb{R}Yi∈R (
revenue) - 特征向量 Xi∈RnX_i \in \mathbb{R}^nXi∈Rn (
age)
我们感兴趣的是估计平均处理效应。
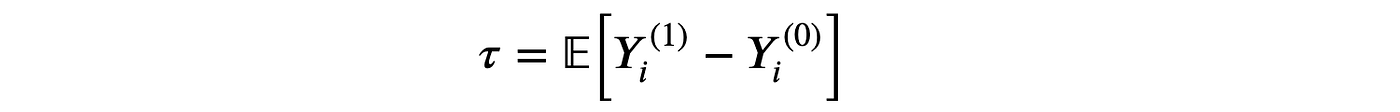
其中 Yi(d)Y_i^{(d)}Yi(d) 表示个体 iii 在处理状态 ddd 下的潜在结果。我们还做出以下假设。
假设1:无混淆性(或可忽略性,或基于可观测变量的选择)
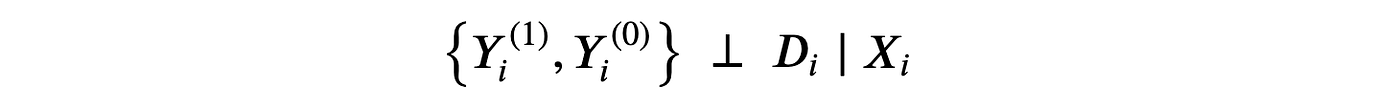
即,在可观测特征 XXX 的条件下,处理分配 DDD 相当于随机的。我们实际假设的是,没有我们未观察到的其他特征会同时影响用户是否获得 premium 功能及其 revenue。这是一个强假设,观察到的个体特征越多,就越有可能满足。
假设2:稳定单元处理值假设 (SUTVA)
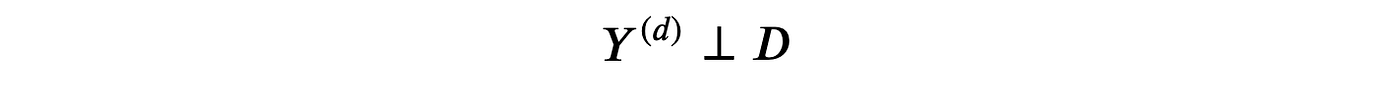
即,潜在结果不依赖于处理状态。在我们的案例中,我们排除了另一个用户获得 premium 功能可能会影响我的 premium 对 revenue 的影响。SUTVA 最常被违反的情况是存在网络效应:我的朋友使用社交网络会增加我使用它的效用。
2.2 S-学习器 (S-Learner)
最简单的元算法是单一学习器或S-学习器。为了构建S-学习器估计器,我们为所有观测值拟合一个单一模型 μ^\hat{\mu}μ^。
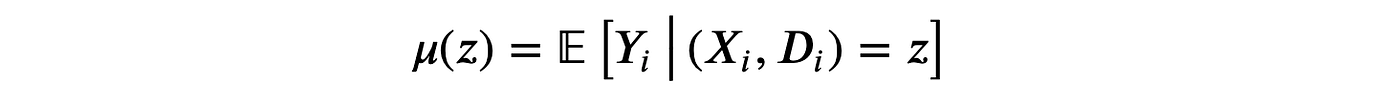
估计器由在有处理 d=1d=1d=1 和无处理 d=0d=0d=0 情况下评估的预测值之差给出。
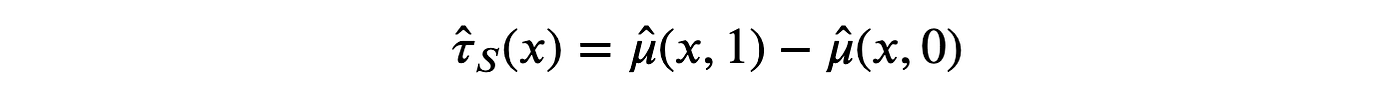
让我们使用 决策树回归 模型来构建S-学习器,使用 sklearn 包中的 DecisionTreeRegressor 函数。我在这里不会深入讨论决策树的细节,但我只会说它是一个非参数估计器,它使用训练数据将状态空间(在我们的例子中是 premium 和 age)分成块,并预测结果(在我们的例子中是 revenue)作为其在每个块内的平均值。
from sklearn.tree import DecisionTreeRegressormodel = DecisionTreeRegressor(min_impurity_decrease=0.001)
S_learner(dgp, model, y="revenue", D="premium", X=["age"])
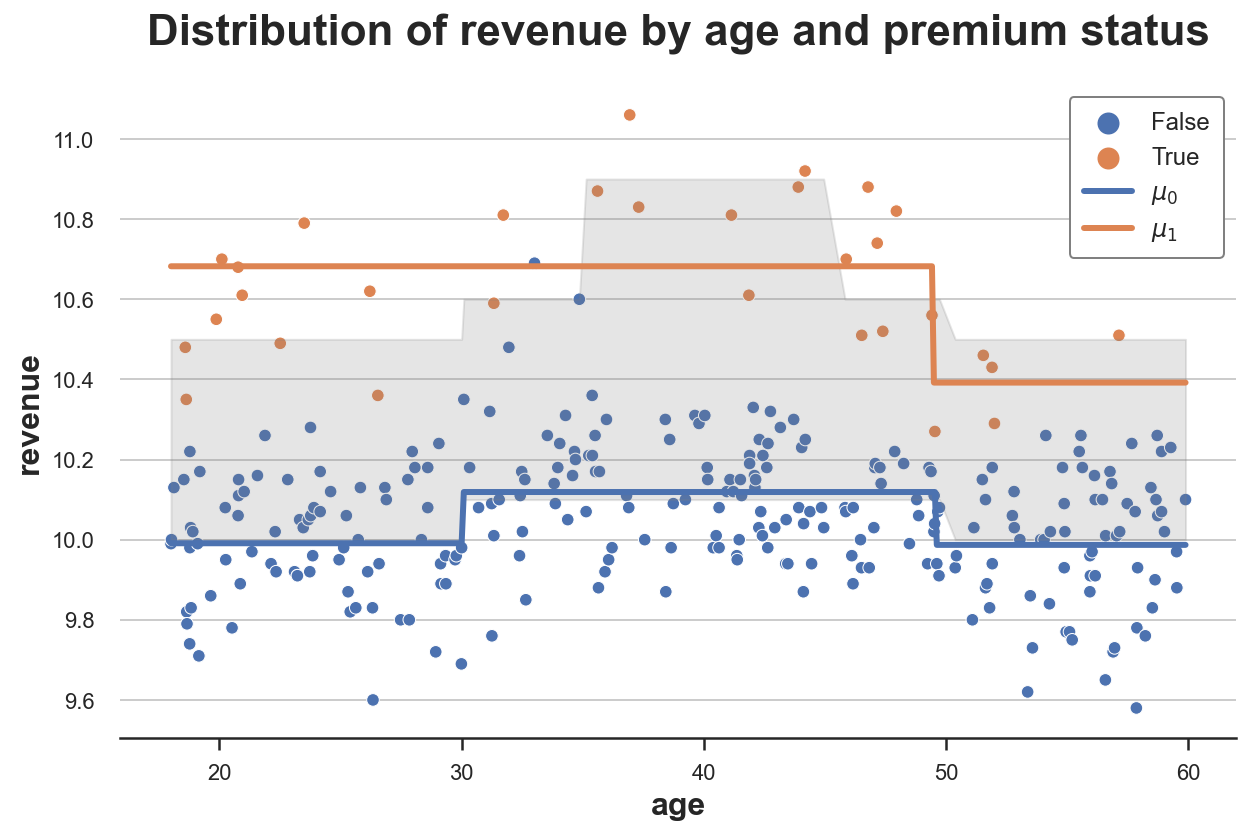
该图描绘了数据以及响应函数 μ^(x,1)\hat{\mu}(x,1)μ^(x,1) 和 μ^(x,0)\hat{\mu}(x,0)μ^(x,0)。我还用灰色绘制了真实响应函数之间的区域:真实处理效应。
正如我们所看到的,S-学习器足够灵活,能够理解处理组和对照组之间存在水平差异(我们有两条独立的线)。它也很好地捕捉了对照组的响应函数 μ^(x,0)\hat{\mu}(x,0)μ^(x,0),但对处理组的响应函数 μ^(x,1)\hat{\mu}(x,1)μ^(x,1) 捕捉得不太好。
S-学习器的问题在于它正在学习一个单一模型,所以我们必须希望该模型能揭示处理 DDD 中的异质性,但这可能并非如此。此外,如果模型由于 XXX 的高维度而受到严格正则化,它可能无法恢复任何处理效应。例如,对于决策树,我们可能不会在处理变量 DDD 上进行分割。
2.3 T-学习器 (T-Learner)
为了构建双学习器或T-学习器估计器,我们拟合两个不同的模型,一个用于处理单元,一个用于控制单元。

估计器由两个模型的预测值之差给出。
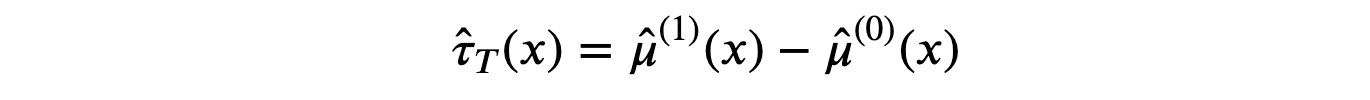
我们像以前一样使用决策树回归模型,但这次,我们为处理组和对照组拟合了两个独立的决策树。
T_learner(dgp, model, y="revenue", D="premium", X=["age"])
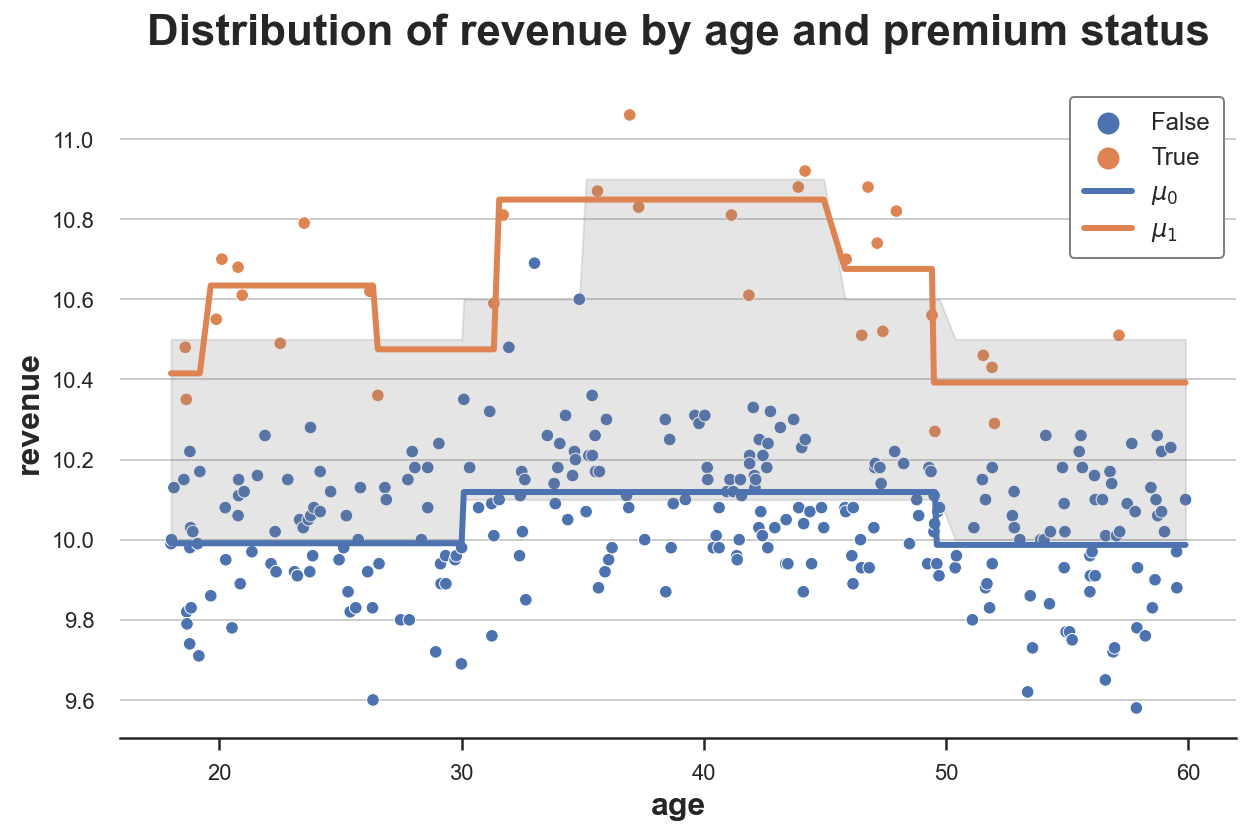
正如我们所看到的,T-学习器比S-学习器更灵活,因为它拟合了两个独立的模型。对照组的响应函数 μ^(0)(x)\hat{\mu}^{(0)}(x)μ^(0)(x) 仍然非常准确,而处理组的响应函数 μ^(1)(x)\hat{\mu}^{(1)}(x)μ^(1)(x) 比以前更灵活。
现在问题是,我们只使用了部分数据来解决每个预测问题,而S-学习器使用了所有数据。通过拟合两个独立的模型,我们失去了一些信息。此外,通过使用两个不同的模型,我们可能会在没有异质性的时候得到异质性。例如,对于决策树,即使数据生成过程相同,我们也很可能会得到不同样本的不同分割。
2.4 X-学习器 (X-Learner)
交叉学习器或X-学习器估计器是T-学习器估计器的扩展。它以以下方式构建:
- 与T-学习器一样,分别为 μ^(1)(x)\hat{\mu}^{(1)}(x)μ^(1)(x) 和 μ^(0)(x)\hat{\mu}^{(0)}(x)μ^(0)(x) 计算独立模型,分别使用处理单元和控制单元。
- 计算中间 Delta 函数为:
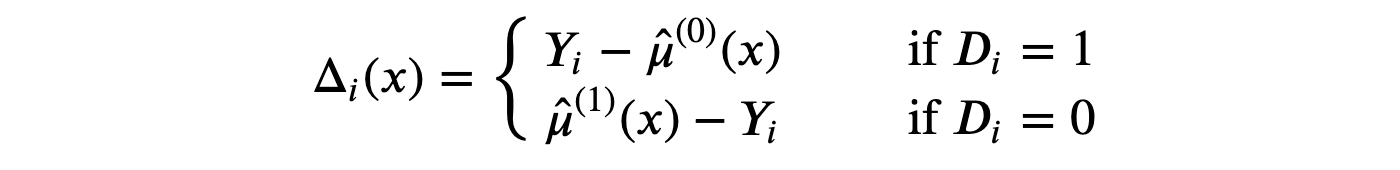
-
从 XXX 预测 Δ\DeltaΔ,从处理单元计算 τ^(1)(x)\hat{\tau}^{(1)}(x)τ^(1)(x),从控制单元计算 τ^(0)(x)\hat{\tau}^{(0)}(x)τ^(0)(x)。
-
估计 倾向得分,即被处理的概率。
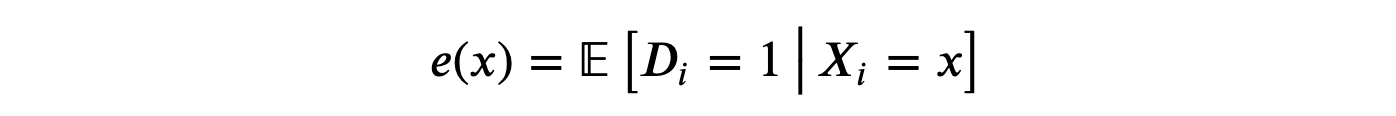
- 计算处理效应:
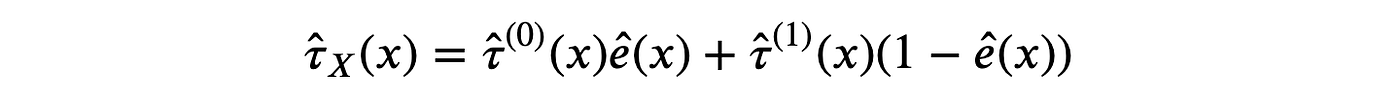
为了更好地理解X-学习器的工作原理,我们想像以前一样绘制响应函数。然而,该方法不直接依赖于响应函数。我们仍然可以恢复伪响应函数吗?是的!
首先,我们可以将处理效应重写为:
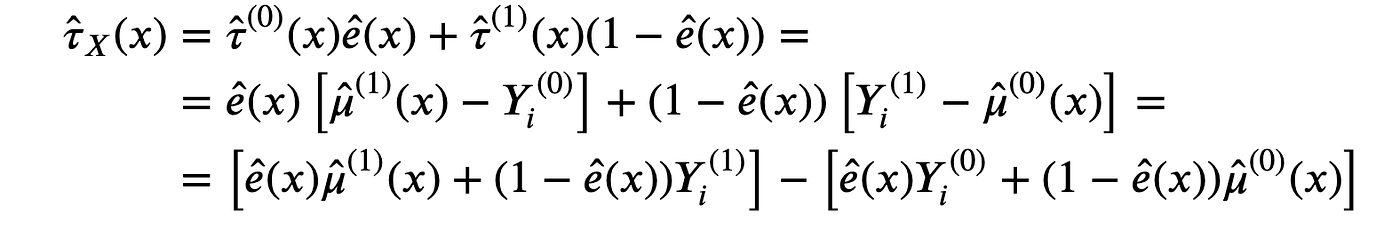
这样,X-学习器估计的伪响应函数为:
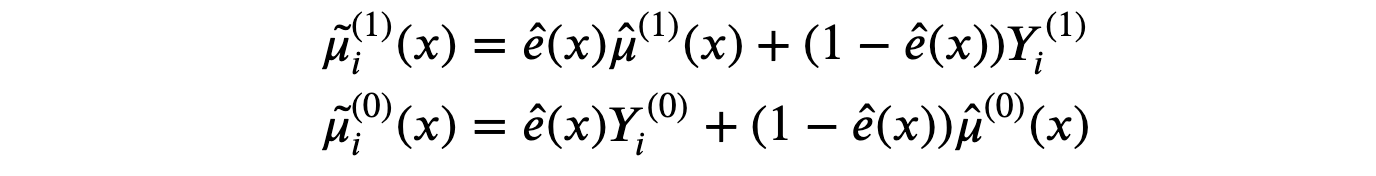
正如我们所看到的,X-学习器将真实值 Yi(d)Y_i^{(d)}Yi(d) 与估计值 μ^i(d)(x)\hat{\mu}_i^{(d)}(x)μ^i(d)(x) 结合起来,通过 倾向得分 ei(x)e_i(x)ei(x)(即估计的处理概率)进行加权。
这意味着什么? 这意味着如果对于某些可观测变量,我们可以清楚地将处理组和对照组分开,那么控制响应函数 μ^i(d)\hat{\mu}_i^{(d)}μ^i(d) 将获得大部分权重。相反,如果两组无法区分,实际结果 Yi(d)Y_i^{(d)}Yi(d) 将获得大部分权重。
为了说明该方法,我将通过使用最近邻观测值来近似 Yi(d)Y_i^{(d)}Yi(d),从而构建伪响应函数,使用 KNeighborsRegressor 函数。我通过 逻辑回归 使用 LogisticRegressionCV 函数估计倾向得分。
X_learner(df, model, y="revenue", D="premium", X=["age"])
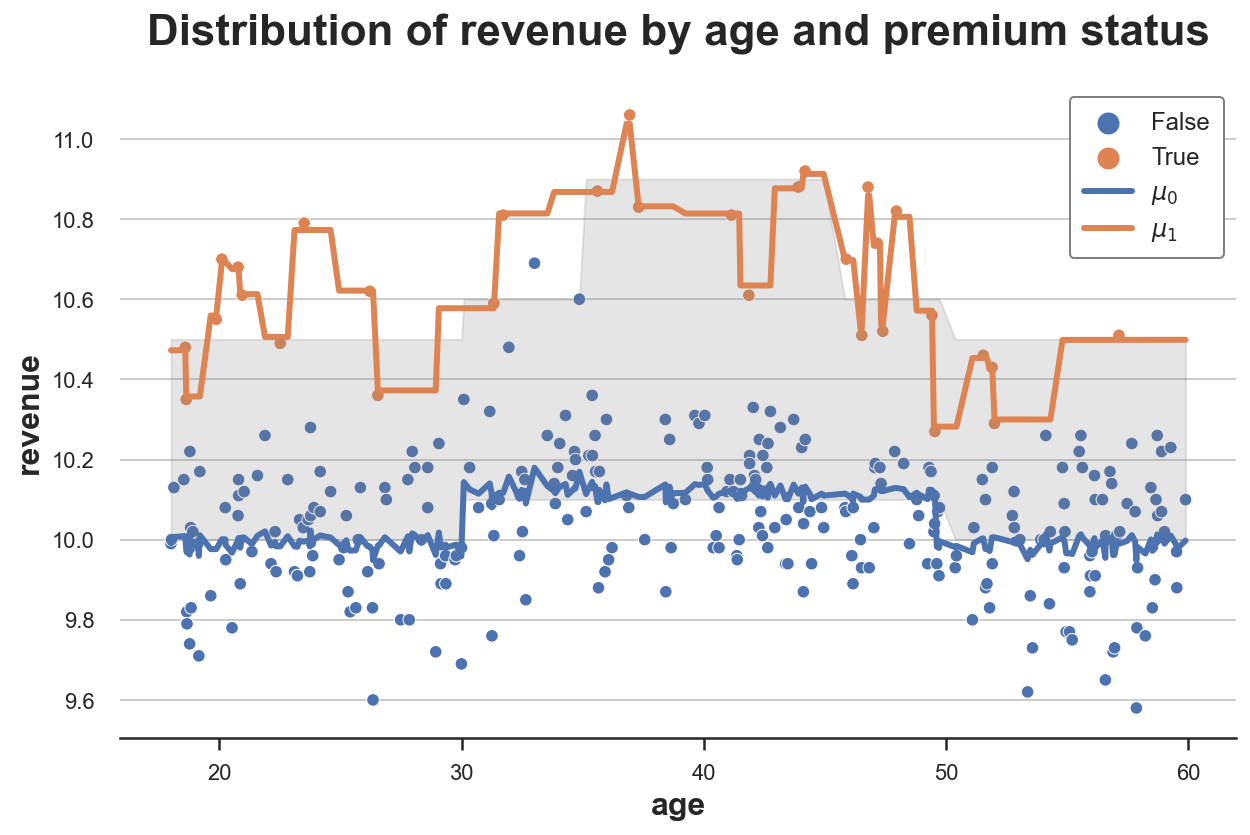
从这张图我们可以清楚地看到,X-学习器的主要优点是它能根据上下文调整响应函数的灵活性。在状态空间中数据量大的区域(对照组),它主要使用估计的响应函数;在数据量小的区域(处理组),它使用观测值本身。
3 结论
在这篇文章中,我们看到了 Künzel, Sekhon, Bickel, Yu, (2019) 引入的不同估计器,它们利用灵活的机器学习算法来估计异质处理效应。这些估计器在复杂性上有所不同:S-学习器拟合一个单一估计器,将处理指示符作为协变量。T-学习器为处理组和对照组拟合两个独立的估计器。最后,X-学习器是T-学习器的扩展,它允许根据处理组和对照组之间可用数据量的不同,提供不同程度的灵活性。
异质处理效应的估计对于处理目标定位至关重要,这在工业界尤为重要。事实上,这方面的研究正在迅速发展并受到广泛关注。在众多其他论文中,值得一提的是 Nie and Wager (2021) 的R-学习器方法以及 Athey and Wager (2018) 的因果树和森林。我将来可能会写更多关于这些方法的文章,敬请期待 ☺️
4 参考文献
111 S. Künzel, J. Sekhon, P. Bickel, B. Yu, Metalearners for estimating heterogeneous treatment effects using machine learning (2019), PNAS.
222 X. Nie, S. Wager, Quasi-oracle estimation of heterogeneous treatment effects (2021), Biometrika.
333 S. Athey, S. Wager, Estimation and Inference of Heterogeneous Treatment Effects using Random Forests (2018), Journal of the American Statistical Association.
5 代码
您可以在此处找到原始 Jupyter Notebook:
https://github.com/matteocourthoud/Blog-Posts/blob/main/notebooks/meta.ipynb
