小杰机器学习高级(two)——极大似然估计、交叉熵损失函数
极大似然估计与交叉熵损失函数
从以下3个方面对激活函数及其导数进行介绍
1.极大似然估计与交叉熵损失函数算法理论讲解
2.编程实例与步骤
3.实验现象
上面这3方面的内容,让大家,掌握并理解极大似然估计与交叉熵损失函数。
1. 极大似然估计与交叉熵损失函数算法理论
交叉熵损失函数是独立于我们的MSE(均方差损失函数)。
交叉熵损失函数是另一种损失函数。MSE损失函数和交叉熵损失函数它们的应用场合是不一样的。
均方差损失函数主要应用在回归、拟合领域。(eg:有一些点用直线拟合它,或者用曲线去拟合)。
交叉熵损失函数主要应用在分类领域?
eg:对有猫和狗的图片进行分类,输入猫和狗的照片,然后特征提取,得到两类结果,可以先用softmax,得到两类的概率值将求解出来的概率,交给交叉熵计算损失?就可以进行模型优化了。
那分类问题指的是什么问题呢?
分类问题是机器学习中最常见的问题之一。分类问题的目标是根据给定的特征将数据分为不同的类别。
分类问题怎么去优化的呢?
主要是使用最小化交叉熵损失去优化。为什么使用最小化交叉熵损失函数,它内在的原因是什么?
MSE(均方差的理论支撑是距离))
交叉熵损失函数的理论依据是什么呢?
其实它的理论依据非常多,有不同的方式可以解释。交叉熵损失函数可以用在我们分类算法上的一个损失函数中,这里用最简单的一个理论依据叫似然估计或者叫极大似然估计。
MSE解决分类问题的弊端?
在回归预测问题中,使用MSE作为损失函数,L2距离(欧式距离)能够很漂亮的体现出预测值与实际值的差距(距离)。
在分类问题中,网络输出的是属于某个类的概率。最后一层使用激活函数进行处理,二分类就使用Sigmoid,多分类使用Softmax,如果使用MSE,当与Sigmoid或Softmax搭配使用时,loss的偏导数的变化趋势和预测值及真实值之间的数值的变化趋势不一致。

也就是说,预测为错误时,依然没有梯度让网络可以学习。可以得出MSE对于分类问题无法有效地度量类别之间的差异,导致对于分类任务的优化不够敏感。
1.1伯努利分布
伯努利分布是一种离散型概率分布,它描述的是一次伯努利试验中成功和失败的概率分布。在伯努利分布中,只有两种可能的结果,通过用0和1来表示,其中0表示失败,1表示成功。
伯努利分布的数学公式表达如下:
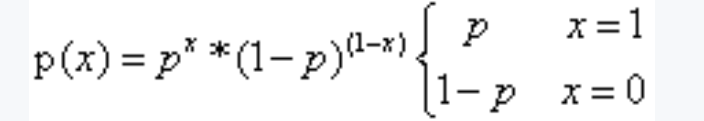
如果表示抛硬币,则正面向上的概率为x=1时,p(1)=p^1*(1-p)^(1-1)=p,
反面向上的概率为x=0时,p(0)=p^0*(1-p)=1-p
1.2二项分布
二项分布是描述了n次独立的伯努利试验中成功的次数的概率分布。在二项分布中,每次试验都是独立的,且成功和失败的概率保持不变。二项分布的概率质量函数公式如下:
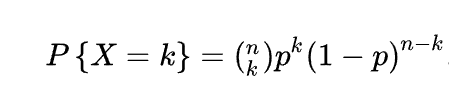
其中n表示试验次数,k表示成功的次数,p表示单次实验成功的概率。
1.3极大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值。
假设现在进行伯努利试验10次,结果用随机变量xi表示,则x1,x2,...x10,满足独立同分布。其值为(1,0,1,0,0,0,1,0,0,0),每个样本出现的概率的乘积为:
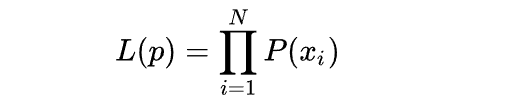
对于上面的例子结果为:
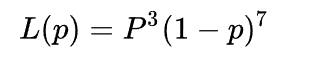
极大似然估计的目标是不是要求最大的P值?
举个例子(p=0.1 L(p)=0.0004782969
p=0.2 L(p)=0.0016777216
p=0.5 L(p)=0.0009765625 )
怎么求最大的p值呢?
1.3.1 连乘变连加
通过取对数(log的底数为e),将连乘变成连加,方便计算。
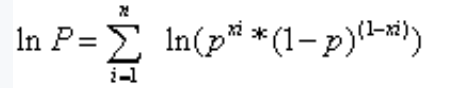
将xi带入得到如下公式:
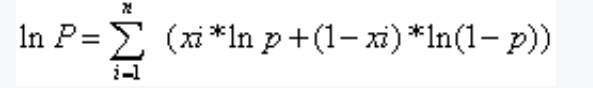
对上面求导,然后通过求导数,令导数等于零来解方程,找到使得对数似然函数最大化的参数值p。
1.4最小化损失函数
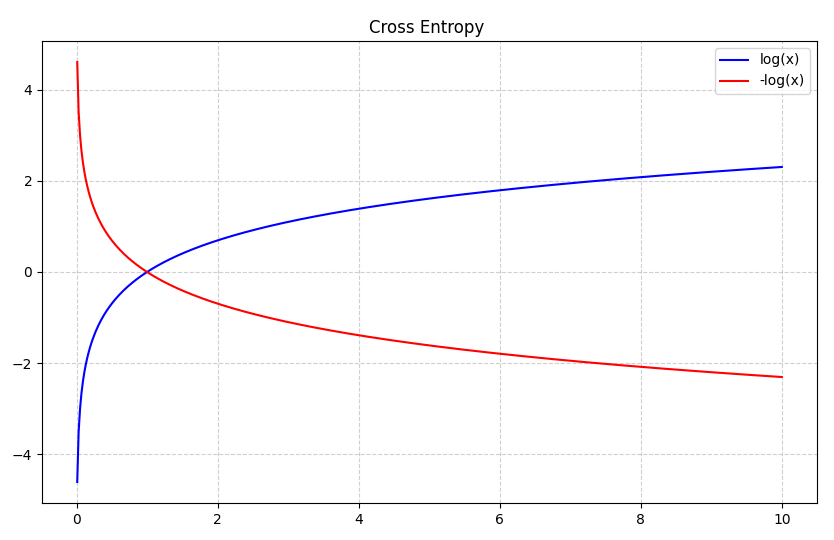
1.4.1交叉熵
交叉熵(Cross Entropy)是一种用于衡量两个概率分布之间差异的度量方法。在机器学习中,交叉熵常用于衡量模型的预测结果与真实标签之间的差异,交叉熵越小,两个概率分布就越接近,即拟合的更好。
交叉熵的计算公式
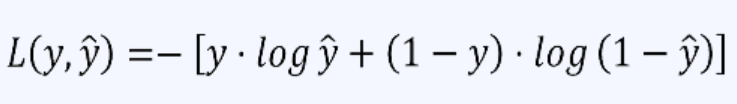
其中,y 是真实标签, y_hat是模型预测的概率值。
通过上面的讲解,发现对极大似然估计公式前面加上负号,使用负对数似然函数来定义损失函数和交叉熵公式一样(通常称为交叉熵损失函数),这样就将最大化似然函数转化为最小化损失函数的问题。这样,在求解优化问题时,可以使用梯度下降等优化算法来最小化负对数似然函数(或交叉熵损失函数),从而得到最大似然估计的参数值。
二分类交叉熵
在二分类情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为p和1-p,此时表示式为(log的底数为e):

多分类交叉熵
多分类交叉熵就是对二分类的交叉熵的扩展,在计算公式中和二分类稍微有些区别,但是还是比较容易理解,具体公式如下所示:

补充:交叉熵怎么衡量损失的。