最优控制3 -- 动态规划-一个解析解的例子

---

前言

本系列是个人在b站大学学习【DR_CAN】的最优控制教程的笔记，主要用于记录和方便随时知识回顾。

感谢DR_CAN精彩的讲解，附bilibili视频链接：【最优控制-合集】

---

这节很简单，但是超级重要！超级重要！超级重要！ 我希望大家可以自己动手推一下，这样印象深刻一些。这是LQR/iLQR的基础，对于理解LQR/iLQR算法的递推很有帮助。

正文

上一节讨论了贝尔曼最优理论，并讨论了使用数值方法求解最优解的过程，这一节将从一个简单的例子讲解动态规划的解析方法。

考虑一个单输入，单状态的例子。计算2步后系统达到目标状态的最优控制的代价。

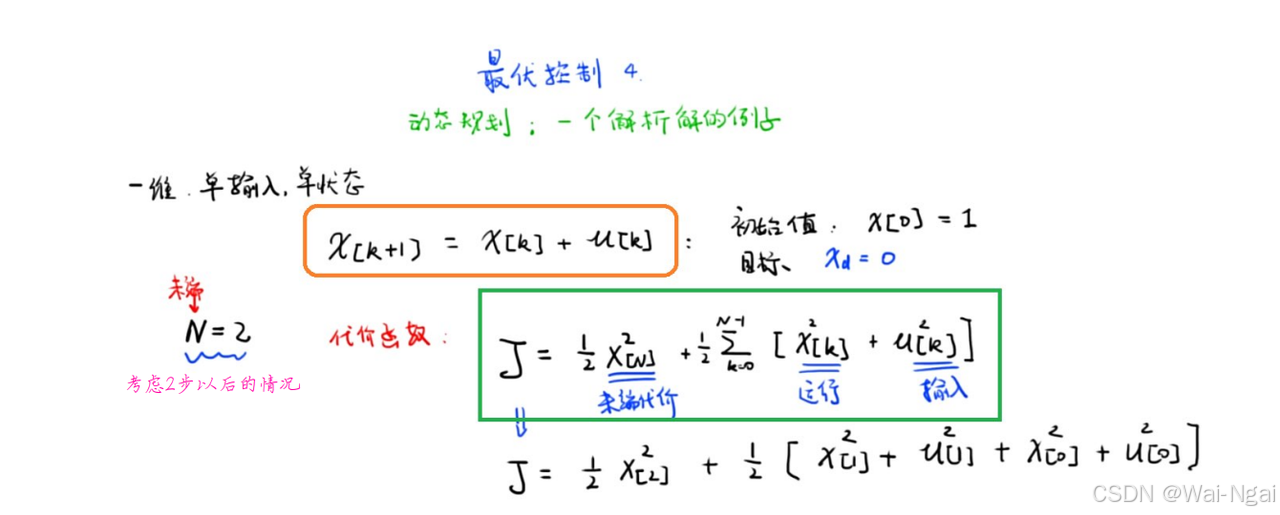
很显然，可以给两个特殊的策略，直接计算出N=2时的代价。

那么如何得到最优的控制序列，使得代价最小呢？下面采用解析的方法。

可以采用逆向分级的思路，先计算$J_{1\to 2}$，再计算$J_{0\to 2}$

将上面的最优控制策略，带入代价函数，可以得到最优的代价：0.8

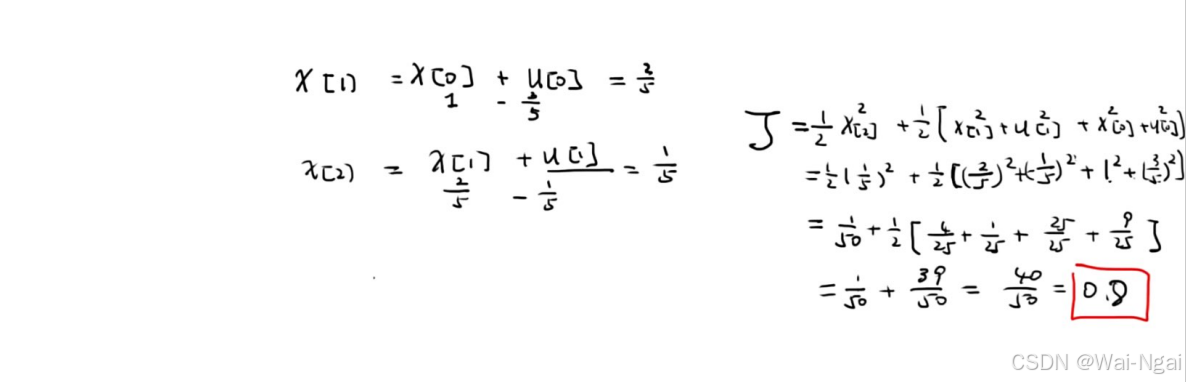
这是一个递归的过程。